Метод искусственного базиса

Симплексный метод решения задач базируется на введении дополнительных переменных, позволяющих образовывать базис. Наличие базиса является необходимым условием при решении задач симплексным методом.

Если же ограничения задачи заданы в виде неравенств вида 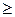или уравнений

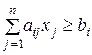и (или) ,

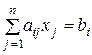то невозможно сразу получить начальное базисное решение, если матрица, составленная из коэффициентов при неизвестных системы ограничений, не позволяет образовывать единичную матрицу. Причем уравнения отражают жесткие условия ограничений по ресурсам, не допускающие никаких отклонений. Для соблюдения равенств вводятся искусственные переменные 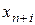, равные нулю. Векторы искусственных переменных образуют необходимую для решения единичную матрицу (базис). Такой базис называется искусственным, а метод решения называется методом искусственного базиса. Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.

Рассмотрим примеры постановок задач такого рода.

Преобразование ограничений, заданных в виде уравнений, рассмотрим на примере:

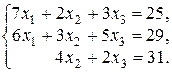
В систему равенств вводим искусственные переменные 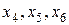с коэффициентами, равными единице, позволяющими образовать искусственный базис:

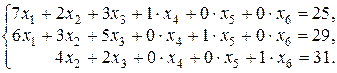
Здесь .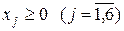

Целевая функция имеет вид:

при решении задачи на максимум –

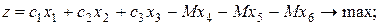
при решении задачи на минимум –

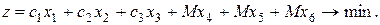
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый «штраф» величиной М, очень большое положительное число, которое обычно не задается .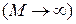

Преобразование ограничений в виде неравенств вида 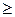рассмотрим на примере:

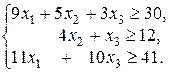
Для получения системы уравнений вводим дополнительные переменные .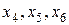

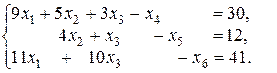
Поскольку в этой системе уравнений отсутствует базис, то вводим в нее искусственные переменные 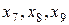с коэффициентами, равными + 1, которые образуют искусственный базис

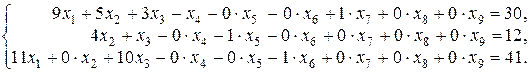
Целевая функция имеет вид:

при решении задачи на максимум –

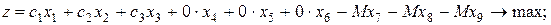
при решении задачи на минимум –

.

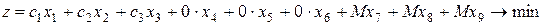Здесь .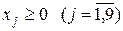

Преобразование разнородных ограничений, представляющих собой смесь уравнений и неравенств разного вида, заключается в образовании базиса решения путем одновременного введения дополнительных и искусственных переменных.

Пример.Определить минимальное значение целевой функции

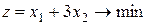
при следующих смешанных условиях-ограничениях:

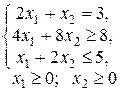
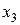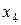Запишем систему ограничений в виде равенств, для чего введем дополнительные переменные и , в результате получим следующую систему:

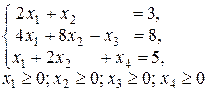
Теперь введем искусственные переменные 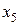и 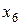в первое и второе уравнения:

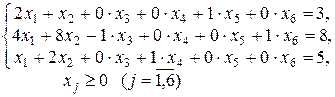
Целевая функция запишется в виде:

.

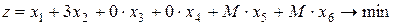Применим к полученной задаче симплексный метод, реализацию которого осуществим с помощью симплексных таблиц.

Поскольку решается задача на минимум, то ключевым столбцом в первой симплексной таблицы будет 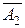, а все остальные преобразования проводятся по стандартной схеме до тех пор, пока в индексной строке не получатся только неположительные числа 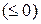, а в оптимальном решении должны отсутствовать положительные значения искусственных переменных 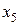и .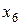

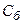	Б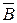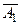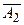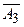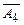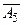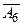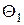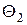
				М	М
М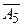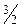
М		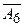			-1
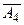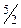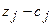	11М		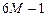	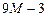-М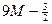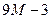
М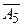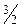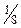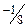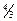
										-
								-	-

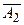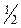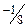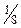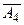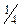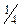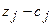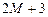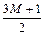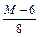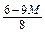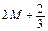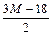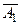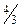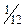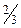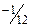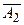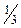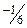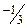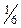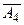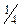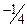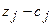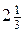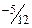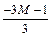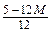Оптимальному плану соответствует точка с координатам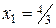и и , .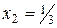

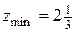Следует заметить, что эту задачу можно решить с помощью графоаналитического метода.