Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.
В случае, когда последовательность частичных сумм положительного ряда неограничена, будем говорить, что его сумма равна 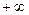 .
.
При доказательстве расходимости гармонического ряда мы, по существу, доказали, что последовательность его частичных сумм неограничена. В качестве другого примера прямого применения этого признака рассмотрим ряд Дирихле (или обобщённый гармонический ряд)
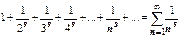 . (18.3.1)
. (18.3.1)
Если s<1, то 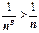 , и, так как частичные суммы
, и, так как частичные суммы 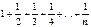 неограничены, то суммы
неограничены, то суммы 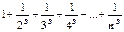 и подавно неограничены, т.е. при s<1 ряд (18.3.1) расходится. Пусть теперь s>1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2:
и подавно неограничены, т.е. при s<1 ряд (18.3.1) расходится. Пусть теперь s>1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2: 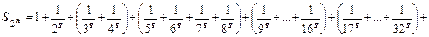 …+
…+ 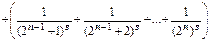 .Структура каждой скобки:
.Структура каждой скобки: 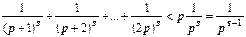 , поэтому
, поэтому 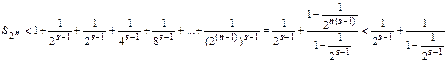 (мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.
(мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.
Итак, ряд Дирихле (18.3.1) сходится при s>1, расходится при s 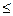 1.
1.
3. Признаки сравнения рядов с положительными членами (док-во 1-го и 2-го признаков).
Признак сравнения.Пусть даны два положительных ряда 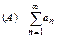 и
и 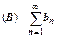 , для которых, хотя бы начиная с некоторого места (при n>N), выполняется неравенство
, для которых, хотя бы начиная с некоторого места (при n>N), выполняется неравенство 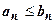 . Тогда: если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В). Другими словами, из сходимости большего ряда следует сходимость меньшего ряда, из расходимости меньшего ряда следует расходимость большего ряда. Сразу отметим, что из расходимости большего ряда, как и из сходимости меньшего ряда, никаких выводов о сходимости второго ряда сделать нельзя.
. Тогда: если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В). Другими словами, из сходимости большего ряда следует сходимость меньшего ряда, из расходимости меньшего ряда следует расходимость большего ряда. Сразу отметим, что из расходимости большего ряда, как и из сходимости меньшего ряда, никаких выводов о сходимости второго ряда сделать нельзя.
Доказательство этого утверждения непосредственно следует из сформулированного в начале раздела признака сходимости положительных рядов: если сходится больший ряд, то последовательность его частичных сумм ограничена, следовательно, ограничена последовательность частичных сумм меньшего ряда, следовательно, меньший ряд сходится; если расходится меньший ряд, то последовательность его частичных сумм неограничена, следовательно, неограничена последовательность частичных сумм большего ряда, следовательно, больший ряд расходится.
Предельная форма признака сравнения. Если существует конечный 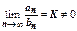 , то ряды (А) и (В) сходятся или расходятся одновременно.
, то ряды (А) и (В) сходятся или расходятся одновременно.
Доказательство. По определению предела для 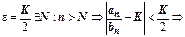
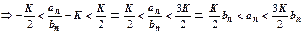 . Последнего неравенства достаточно для доказательства всех утверждений теоремы.
. Последнего неравенства достаточно для доказательства всех утверждений теоремы. 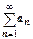 сходится
сходится 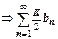 сх-ся
сх-ся 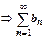 сх-ся. остальные случаи схематично: (А) расх-ся
сх-ся. остальные случаи схематично: (А) расх-ся 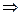 (3К/2 B) расх-ся
(3К/2 B) расх-ся 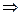 (B) расх-ся; (B) сх-ся
(B) расх-ся; (B) сх-ся 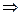 (3К/2 B) сх-ся
(3К/2 B) сх-ся 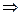 (A) сх-ся; (B) расх-ся
(A) сх-ся; (B) расх-ся 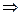 (К/2 B) расх-ся
(К/2 B) расх-ся 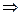 (A) расх-ся.
(A) расх-ся.
4. Признак сходимости Даламбера (с док-вом).
Пусть для положительного ряда существует 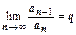 .
.
Тогда если q<1, то ряд сходится,
если q >1, то ряд расходится,
если q=1, то ряд может и сходиться, и расходиться.
Доказательство. 1. Пусть 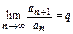 <1. Возьмём
<1. Возьмём 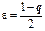 .
. 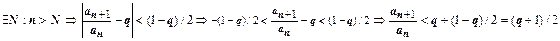 . Если q<1, то число
. Если q<1, то число 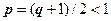 . Итак, при
. Итак, при 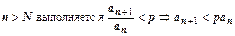 . Выпишем это неравенство для
. Выпишем это неравенство для 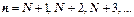 :
: 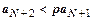 ,
, 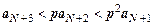 ,
, 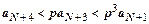 , … ,
, … , 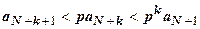 . Все члены ряда, начиная с N+2-го, меньше членов сходящейся геометрической прогрессии, поэтому
. Все члены ряда, начиная с N+2-го, меньше членов сходящейся геометрической прогрессии, поэтому 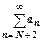 сходится, поэтому
сходится, поэтому 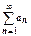 сходится.
сходится.
2. Пусть 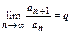 >1. Возьмём
>1. Возьмём 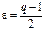 .
. 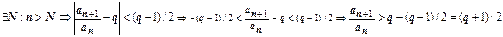 .
.
Если q>1, то число 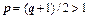 . Итак, при
. Итак, при 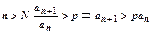 . Выпишем это неравенство для
. Выпишем это неравенство для 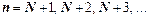 :
: 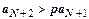 ,
, 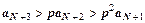 ,
, 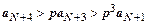 , … ,
, … , 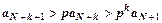 . Все члены ряда, начиная с N+2-го, больше членов расходящейся геометрической прогрессии, поэтому
. Все члены ряда, начиная с N+2-го, больше членов расходящейся геометрической прогрессии, поэтому 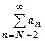 расходится, поэтому
расходится, поэтому 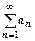 расходится.
расходится.
3. Для рядов 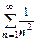 и
и 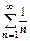 мы опять получим q =1. Первый из этих рядов сходится, второй расходится, но для обоих q=1, т.е. в этом случае вопрос о сходимости ряда действительно остаётся открытым. Признак Даламбера хорошо работает, если общий член ряда содержит факториалы.
мы опять получим q =1. Первый из этих рядов сходится, второй расходится, но для обоих q=1, т.е. в этом случае вопрос о сходимости ряда действительно остаётся открытым. Признак Даламбера хорошо работает, если общий член ряда содержит факториалы.
5. Интегральный признак Коши (с док-вом).
Радикальный признак Коши и признак Даламбера дают q =1 для рядов 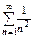 и
и 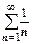 ,
, 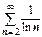 ,
, 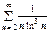 и т.д. Для некоторых из этих рядов оказывается результативным интегральный признак Коши.
и т.д. Для некоторых из этих рядов оказывается результативным интегральный признак Коши.
Теорема.Пусть члены положительного числового ряда 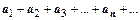 являются значениями непрерывной монотонно убывающей неотрицательной функции
являются значениями непрерывной монотонно убывающей неотрицательной функции 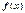 при натуральных значениях аргумента:
при натуральных значениях аргумента: 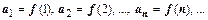 Тогда ряд
Тогда ряд 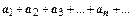 и несобственный интеграл
и несобственный интеграл 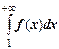 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Обозначим 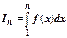 . Согдасно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривой у=
. Согдасно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривой у= 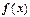 над отрезком [1,n]. Частичная сумма
над отрезком [1,n]. Частичная сумма 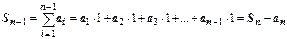 - площадь ступенчатой фигуры, расположенной над криволинейной трапецией (сплошная верхняя граница на рисунке). Сумма
- площадь ступенчатой фигуры, расположенной над криволинейной трапецией (сплошная верхняя граница на рисунке). Сумма 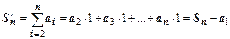 - площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно,
- площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно, 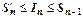 , или
, или 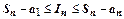 . Из этого неравенства, в котором
. Из этого неравенства, в котором 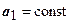 ,
, 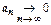 ,
, 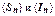 - монотонно возрастающие с ростом n последовательности, и следуют все утверждения теоремы. Например:
- монотонно возрастающие с ростом n последовательности, и следуют все утверждения теоремы. Например:
1. Пусть интеграл 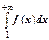 сходится. Это означает, что существует конечный
сходится. Это означает, что существует конечный 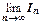 , т.е. последовательность
, т.е. последовательность 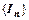 ограничена сверху
ограничена сверху 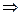 последовательность
последовательность 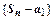 ограничена сверху
ограничена сверху 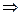 существует конечный
существует конечный 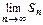 , т.е. ряд
, т.е. ряд 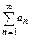 сходится.
сходится.
2. Пусть интеграл 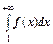 расходится. Это означает, что
расходится. Это означает, что 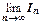 бесконечен, т.е. последовательность
бесконечен, т.е. последовательность 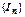 неограничена сверху
неограничена сверху 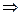 последовательность
последовательность 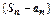 неограничена сверху
неограничена сверху 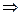 не существует конечного
не существует конечного 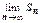 , т.е. ряд
, т.е. ряд 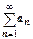 расходится.
расходится.
3, 4. Случаи, когда сходится и расходится ряд, рассмотреть самостоятельно.
Теперь мы можем дать простое доказательство того, что ряд Дирихле 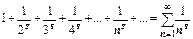 сходится при s>1 и расходится в остальных случаях. Функция
сходится при s>1 и расходится в остальных случаях. Функция 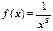 удовлетворяет условиям теоремы: непрерывна, монотонно убывает,
удовлетворяет условиям теоремы: непрерывна, монотонно убывает, 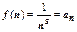 . Интеграл
. Интеграл 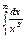 сходится, как мы знаем, при s>1 и расходится при других значениях s, что и требовалось доказать.
сходится, как мы знаем, при s>1 и расходится при других значениях s, что и требовалось доказать.
6. Знакочередующиеся ряды: признак Лейбница (с док-вом). Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков. Несколько изменяя употреблявшуюся выше символику, будем обозначать через an не сам общий член ряда, а его абсолютную величину. Тогда, предполагая для определенности, что первый член знакочередующегося ряда положителен, мы сможем записать этот ряд в форме* a1 - a2 + a3 - a4 + a5 - ... (36)
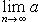 Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.
Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.
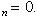 Действительно, допустим, что ряд (36) таков, что a1 > a2 > a3 > a4 > ..., (37) (38)
Действительно, допустим, что ряд (36) таков, что a1 > a2 > a3 > a4 > ..., (37) (38)
Образуем частичные суммы S2n: S2 = (a1 - a2), S4 = (a1 - a2) + (a3 - a4), S6 = (a1 - a2) + (a3 - a4) + (a5 - a6), . . . . . . .
Благодаря (37), все скобки положительны. Значит, S2 < S4 < S6 < ... Иначе говоря, последовательность {S2n} возрастает. С другой стороны, S2n = a1 - (a2 - a3) - (a4 - a5) - ... - (a2n-2 - a2n-1) - a2n, откуда ясно, что S2n < a1.
Как известно, при этих условиях существует конечный предел 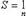
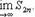 Но S2n+1 = S2n + a2n+1, откуда в связи с (38) вытекает, что сумма S2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма Sn будет сколь угодно близка к S независимо от четности n. Иначе говоря,
Но S2n+1 = S2n + a2n+1, откуда в связи с (38) вытекает, что сумма S2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма Sn будет сколь угодно близка к S независимо от четности n. Иначе говоря, 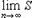
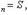 чем и доказана теорема.
чем и доказана теорема.
7. Знакопеременные ряды: понятия абсолютной и условной сходимости, признак абсолютной сходимости, свойства абсолютно и условно сходящихся рядов.
Теперь рассмотрим такие ряды, знаки членов которых уже совершенно произвольны. При этом снова будем обозначать через a1, a2,a3 ... сами члены ряда.
Теорема 1. Сопоставим с рядом a1 + a2 + a3 + ... (39) ряд |a1| + |a2| + |a3| + ..., (40) составленный из абсолютных величин членов данного ряда. Если сходится ряд (40), то сходится и исходный ряд (39).
В самом деле, пусть ряд b1 + b2 + b3 + ... (41) есть ряд, состоящий из всех положительных (или равных нулю) членов нашего ряда (39) [причем их взаимное расположение таково же, как и в ряде (39)]. Пусть, далее, c1 + c2 + c3 + ... (42) есть ряд* абсолютных величин отрицательных членов ряда (39) (также расположенных в том порядке, в котором эти члены следуют друг за другом в исходном ряде).
Каждый из рядов (41) и (42) получается из сходящегося положительного ряда (40) путем вычеркивания части его членов (например, чтобы из (40) получить (41), надо вычеркнуть из (40) числа c1, c2, c3, ...). Поэтому в силу теоремы 4 ряды (41) и (42) сходятся. Обозначим их суммы соответственно через B и C.
Обозначим, далее, через An, Bn и Cn частичные суммы рядов (39), (41) и (42). Пусть среди чисел a1, a2, a3, ..., an имеется m(n) неотрицательных и p(n) отрицательных. Тогда An = Bm(n) - Cp(n). Правая часть этого равенства с ростом n стремится к разности B - C. Значит, и левая часть стремится к тому же пределу. Теорема доказана.
Заметим, что из сходимости ряда (39) не вытекает, что сходится (40). Например, ряд 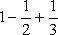
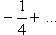 сходится (это следует хотя бы из теоремы Лейбница), но ряд, составленный из абсолютных величин, будучи гармоническим, расходится. Таким образом, требование сходимости ряда (40) представляет собой более тяжелое требование, чем требование сходимости ряда (39). В связи с этим такой ряд (39), который не только сходится сам, но для которого и ряд абсолютных величин, называется абсолютно сходящимся. Если же ряд (39) сходится, но ряд (40) расходится, то говорят, что (39) есть ряд условно сходящийся.
сходится (это следует хотя бы из теоремы Лейбница), но ряд, составленный из абсолютных величин, будучи гармоническим, расходится. Таким образом, требование сходимости ряда (40) представляет собой более тяжелое требование, чем требование сходимости ряда (39). В связи с этим такой ряд (39), который не только сходится сам, но для которого и ряд абсолютных величин, называется абсолютно сходящимся. Если же ряд (39) сходится, но ряд (40) расходится, то говорят, что (39) есть ряд условно сходящийся.
Теорема 2. Если ряд (39) сходится абсолютно, то сходятся также ряды (41) и (42), образованные положительными членами и модулями отрицательных членов этого ряда. Суммы всех трех рядов связаны соотношением A = B - C. (43)
Признак сходимости Даламбера переносится в теорию рядов с членами любых знаков в следующей форме:
Теорема 3. Пусть ряд (39) таков, что существует предел 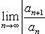
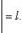 Если l < 1, то ряд сходится, а если l > 1, то расходится.
Если l < 1, то ряд сходится, а если l > 1, то расходится.
Действительно, если l < 1, то по признаку Даламбера будет сходиться ряд абсолютных величин членов данного ряда, а значит, и подавно и сам ряд (39). Если же l > 1, то найдется такое m, что при n ≥ m будет 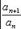
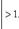
Но тогда |am| < |am+1| < |am+2| < ...,и общий член ряда (39) не стремится к нулю, откуда вытекает расходимость этого ряда.
Теорема 4. От перестановки членов абсолютно сходящегося ряда его абсолютная сходимость не нарушается и сумма не меняется.
Абсолютная сходимость ряда a1 + a2 + a3 + ... (49) означает сходимость положительного ряда |a1| + |a2| + |a3| + ... (50)
Пусть в результате перестановки своих членов ряд (49) превратится в ряд 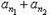
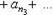 (51)
(51)
Ясно, что ряд абсолютных величин членов ряда (51) получается некоторой перестановкой из ряда (50). Значит, этот ряд абсолютных величин сходится (по предыдущей теореме), а это и означает, что ряд (51) абсолютно сходится.
Введем, далее, ряды b1 + b2 + b3 + ..., (52) c1 + c2 + c3 + ..., (53) состоящие из неотрицательных и модулей отрицательных членов ряда (49). Эти ряды сходятся, и их суммы B и C связаны с суммой A ряда (49) формулой A = B - C. (54)
Когда производим перестановку членов в ряде (49), то это вызывает соответствующие перестановки в рядах (52) и (53), т. к. в этих рядах порядок членов такой же, как и в (49). Но так как ряды (52) и (53) - положительные, то их суммы B и C от перестановки не меняются. С другой стороны, сумма ряда (51) должна выражаться через суммы рядов, полученных упомянутыми перестановками из (52) и (53), той же формулой (54). Отсюда и видно, что сумма ряда (51) равна сумме ряда (49).
Условие абсолютной сходимости ряда для законности перестановок его членов не только достаточно, но и необходимо. Действительно, имеет место Теорема 5. Если ряд (49) сходится неабсолютно, то его члены можно переставить так, чтобы вновь полученный ряд имел любую наперед заданную сумму, а также так, чтобы он расходился.
Теорема 6. Если ряды (56) и (57) сходятся абсолютно и их суммы соответственно равны A и B, то и ряд (58) сходится абсолютно и сумма его C равна произведению сумм рядов (56) и (57) C = AB. (60) Иными словами, абсолютно сходящиеся ряды можно перемножать, как конечные суммы.
8. Степенные ряды: радиус, интервал, область сходимости. Свойства степенных рядов. Теорема Абеля (с док-вом).
Степенным рядом называется ряд вида c0 + c1x + c2x2 + c3x3 + ..., (1) где c0, c1, c2, ... - постоянные числа, называемые коэффициентами ряда. Про ряд (1) говорят, что он расположен по степеням x.
Лемма Абеля. Если степенной ряд (1) сходится при некотором значении x0 ≠ 0, то он абсолютно сходится при каждом x, у которого | x | < | x0 |. (6) В самом деле, так как общий член сходящегося ряда 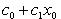
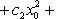
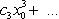
стремится к нулю с возрастанием своего номера, то 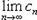
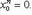 Но если какая-нибудь последовательность имеет предел, то множество членов этой последовательности ограничено. Поэтому существует такое число M, что
Но если какая-нибудь последовательность имеет предел, то множество членов этой последовательности ограничено. Поэтому существует такое число M, что 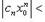
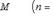
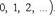 (7) Заметив это, рассмотрим ряд (1) при значении x, удовлетворяющем неравенству (6). Этот ряд можно переписать так:
(7) Заметив это, рассмотрим ряд (1) при значении x, удовлетворяющем неравенству (6). Этот ряд можно переписать так:
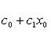
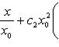
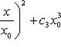
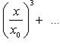 (8)
(8)
В силу (7) ряд, состоящий из абс.величин членов последнего ряда, имеет мажорантный ряд 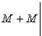
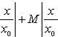
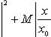
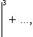
а так как этот ряд сходится (т. к. это есть геометрическая прогрессия со знаменателем 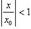 ), то ряд (8), или, что то же самое, ряд (1), сходится абсолютно. Лемма доказана/
), то ряд (8), или, что то же самое, ряд (1), сходится абсолютно. Лемма доказана/
Опр-е. 1) Степенной ряд сходится абсолютно на некотором интервале 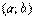 . Иными словами, если мы выбираем любое значение «икс» из интервала
. Иными словами, если мы выбираем любое значение «икс» из интервала 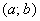 и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал
и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал 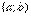 и называется интервалом сходимости степенного ряда. Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
и называется интервалом сходимости степенного ряда. Радиус сходимости, если совсем просто, это половина длины интервала сходимости: 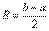
В точках 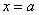 ,
, 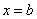 степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: 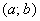
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости рядапредставляет собой полуинтервал: 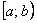 или
или 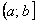 .
.
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: 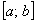
Термины очень похожи, область сходимости ряда – это чуть более детализированныйинтервал сходимости ряда.
2) Степенной ряд сходится абсолютно при любом значении 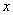 . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получитсяабсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают:
. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получитсяабсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 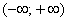 . Радиус сходимости:
. Радиус сходимости: 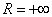 .
.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид 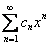 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 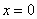 . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: 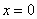 . Если ряд имеет вид
. Если ряд имеет вид 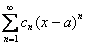 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 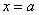 , если ряд имеет вид
, если ряд имеет вид 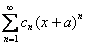 , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:
, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: 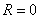 .
.
http://www.pm298.ru/post14.php
