Обратные тригонометрические функции
Обратные функции
Определение:
Если функция монотонна на множестве Х, то она обратима (т.е. имеет обратную функцию).
На интервале монотонности прямая и обратная функции имеют взаимообратные области определения и области значений:
- прямая функция 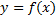 : ООФ -
: ООФ - 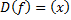 ; ОЗФ -
; ОЗФ - 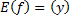 .
.
- обратная функция 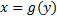 : ООФ -
: ООФ - 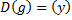 ; ОЗФ -
; ОЗФ - 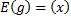 .
.
Свойства прямой и обратной функции:
1. Если прямая функция возрастает (убывает) на множестве определения 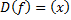 ,
,
то и обратная функция возрастает(убывает) на своём множестве определения 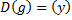 .
.
2. Если функция имеет промежутки и убывания и возрастания, то обратная функция будет определена только на одном из промежутков: или убывания или возрастания.
3. Графики прямой и обратной функций симметричны относительно прямой 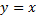 .
.
Пример 1. Построить обратную функцию для функции 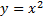 .
.
Решение:
1) Из уравнения исходной функции выражаем переменную 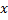 через через 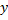 : : | 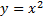 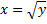 |
2) В системе координат хОу строим исходную функцию 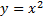 и прямую
и прямую 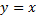 , симметрично которой будем строить обратную функцию;
, симметрично которой будем строить обратную функцию;
3) Относительно прямой 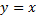 строим симметричные точки.
строим симметричные точки.
Учитываем, что для обратной функции 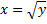 допустимые значения
допустимые значения 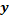 могут быть только положительные, так как арифметический квадратный корень не существует из отрицательных чисел.
могут быть только положительные, так как арифметический квадратный корень не существует из отрицательных чисел.
4) По симметричным точкам–двойникам проводим линию графика обратной функции
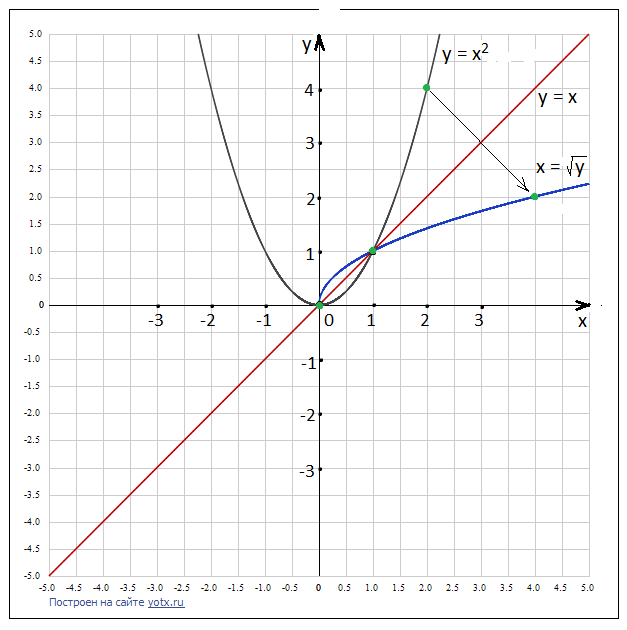 | для исходной функции 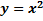 имеет промежутки и убывания и возрастания имеет промежутки и убывания и возрастания 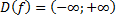 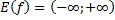 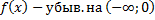 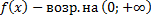 обратная функция обратная функция 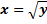 определена только на промежутке возрастания определена только на промежутке возрастания 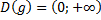 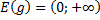 . . |
Есть функции, которые симметричны сами себе.
Например:
| 1) Исходная функция | Обратная функция |
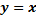 – монотонно возрастает – монотонно возрастает | 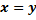 |
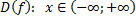 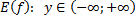 | 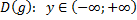 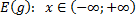 |
| 2) Исходная функция | Обратная функция |
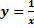 – монотонно убывает – монотонно убывает | 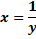 |
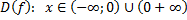 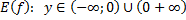 | 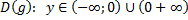 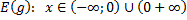 |
Пример 2. Построить обратную функцию для функции 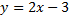 .
.
Решение:
1) Из уравнения исходной функции выражаем переменную 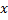 через через 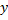 : : | 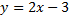 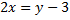 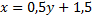 |
2) В системе координат хОу строим исходную прямую 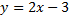 и прямую
и прямую 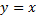 , симметрично которой будем строить обратную функцию;
, симметрично которой будем строить обратную функцию;
3) Относительно прямой 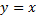 строим симметричные точки.
строим симметричные точки.
4) По симметричным точкам–двойникам проводим линию графика обратной функции
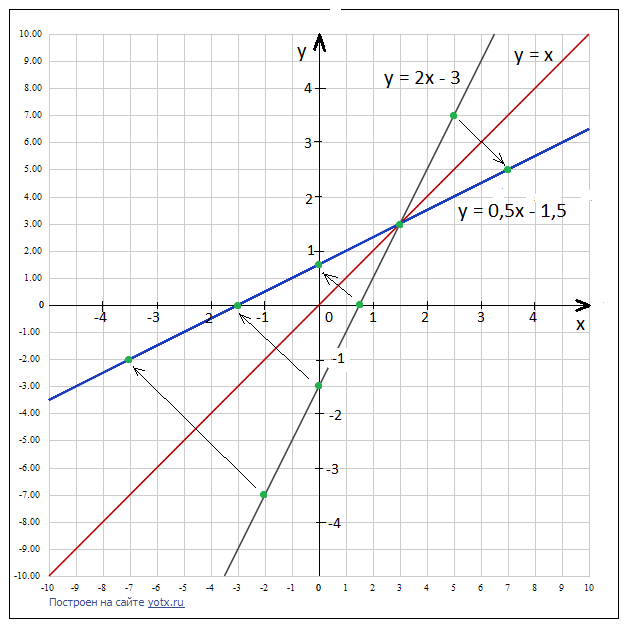 | для исходной функции 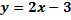 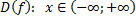 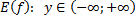 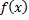 – монотонно возрастает для обратной функции – монотонно возрастает для обратной функции 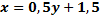 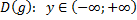 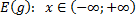 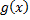 – монотонно возрастает – монотонно возрастает |
Существуют пары функций, которые симметричны друг другу.
Например, для показательной функции обратной является логарифмическая. А для логарифмической обратной является показательная функция.
Пример 3. Построить обратную функцию для функции 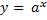 ( рассмотрим пример для
( рассмотрим пример для 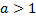 )
)
Решение:
1) Из уравнения исходной функции выражаем переменную 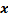 через через 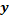 : : | 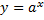 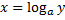 |
2) В системе координат хОу строим функцию 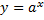 и прямую
и прямую 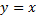 ;
;
3) Относительно прямой 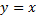 строим симметричные точки, учитывая, что обратная функция имеет ограничения
строим симметричные точки, учитывая, что обратная функция имеет ограничения 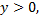
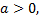
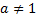 .
.
4) По симметричным точкам–двойникам проводим линию графика обратной функции
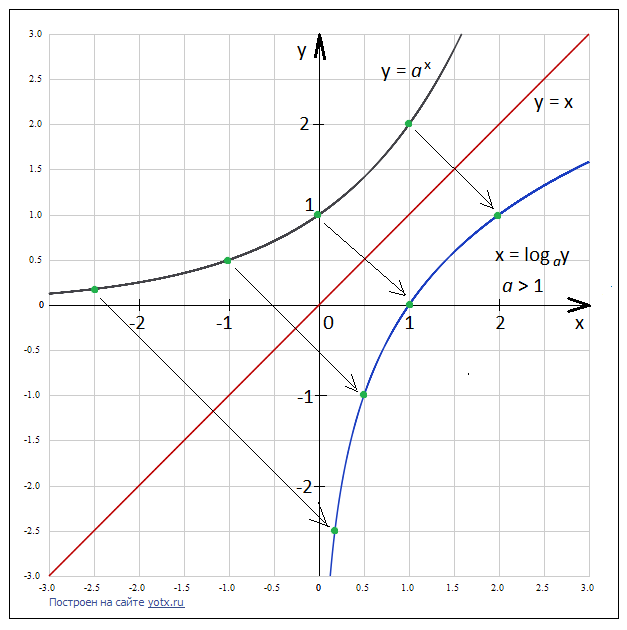 | для исходной функции 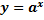 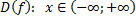 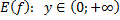 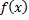 – монотонно возрастает для обратной функции – монотонно возрастает для обратной функции 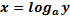 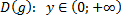 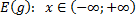 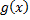 – монотонно возрастает – монотонно возрастает |
Пример 4. Построить обратную функцию для функции 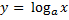 (рассмотрим пример для
(рассмотрим пример для 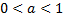 )
)
Решение:
1) Из уравнения исходной функции выражаем переменную 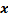 через через 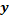 : : | 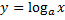 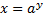 |
2) В системе координат хОу строим функцию 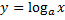 и прямую
и прямую 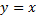 ;
;
3) Относительно прямой 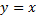 строим симметричные точки
строим симметричные точки
4) По симметричным точкам–двойникам проводим линию графика обратной функции
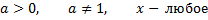
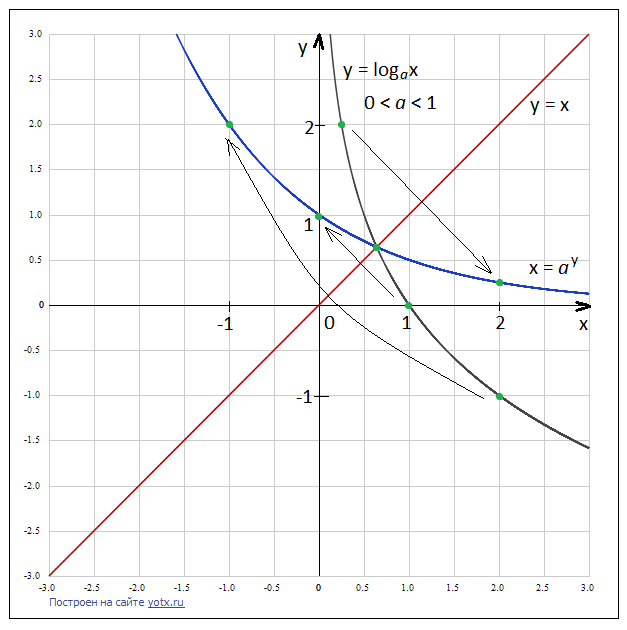 | для исходной функции 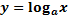 , , 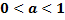 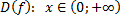 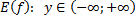 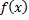 – монотонно убывает для обратной функции – монотонно убывает для обратной функции 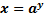 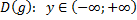 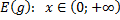 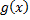 – монотонно убывает – монотонно убывает |
Обратные тригонометрические функции
Обозначение:
Для 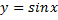 | обратная -арксинус 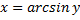 или или 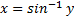 |
Для 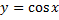 | обратная -арккосинус 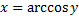 или или 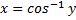 |
Для 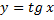 | обратная -арктангенс 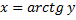 или или 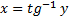 |
Для 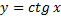 | обратная -арккотангенс 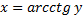 или или 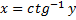 |
Назначение: Обратные тригонометрические функции переводят числовое значение функции в градусную или радианную меру угла. Например:
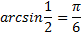 | так как 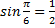 |
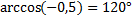 | так как 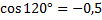 |
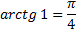 | так как 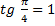 |
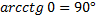 | так как  |
| Прямые тригонометрические функции переводят градусную (или радианную) меру угла в число. |
Построение обратных тригонометрических функций:
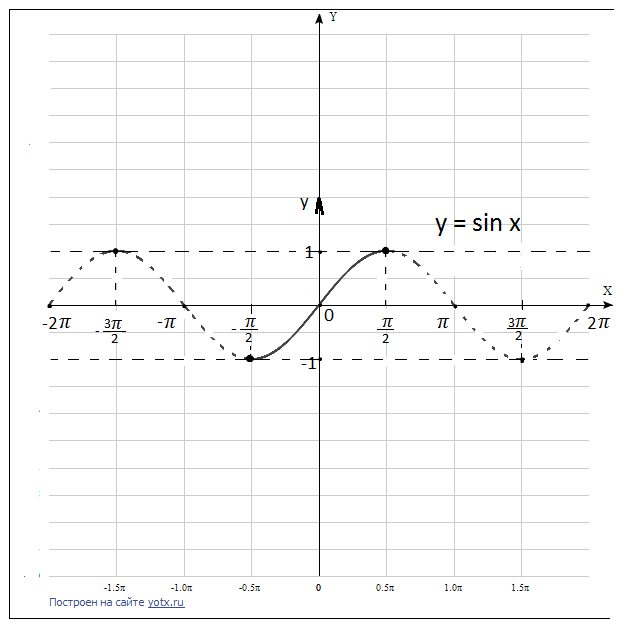
Тригонометрические функции являются периодичными и поэтому одно и то же значение у соответствует разным значениям х. Например:
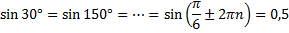
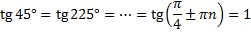
Кроме того, функции синуса и косинуса имеют множественные промежутки убывания и возрастания. Для этих функций нужно выбрать главный промежуток возрастания (или убывания) и для него строить обратную функцию.
Главные промежутки возрастания (убывания) для тригонометрических функций:
Для 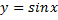 | промежуток возрастания 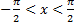 |
Для 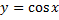 | промежуток убывания 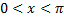 |
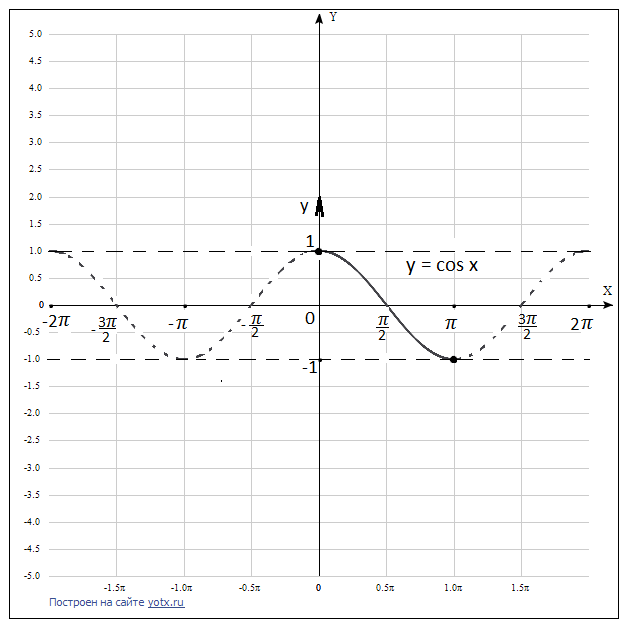
Для 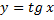 | промежуток возрастания 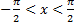 |
Для 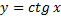 | промежуток убывания 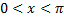 |
Важно! При определении обратной функции уже отмечалось, что ООФ и ОЗФ прямой и обратной функции взаимообратные. При построении графиков обратных тригонометрических функций значения оси Ох и Оу меняются.
 | 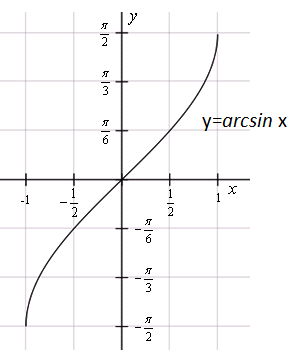 |
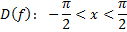 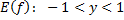 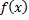 – монотонно возрастает – монотонно возрастает | 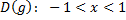 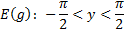 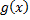 – монотонно возрастает – монотонно возрастает |
 | 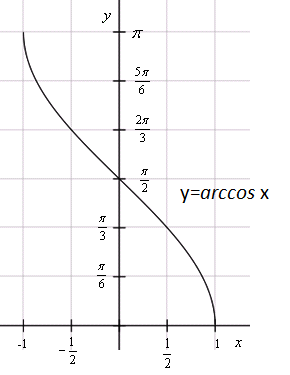 |
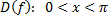 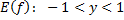 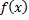 – монотонно убывает – монотонно убывает | 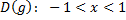 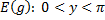 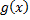 – монотонно убывает на промежутке – монотонно убывает на промежутке |
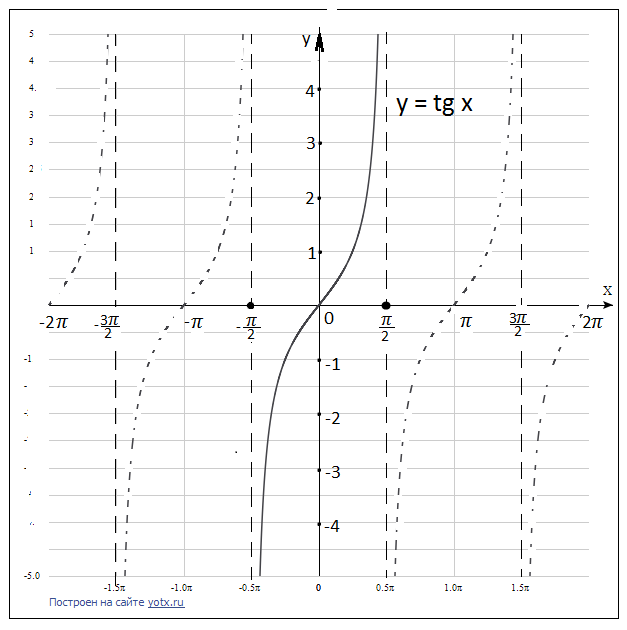 | 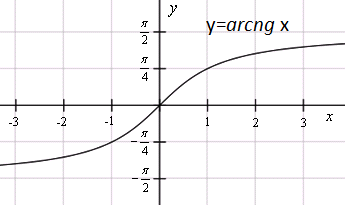 |
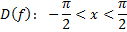 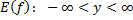 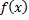 – монотонно возрастает – монотонно возрастает | 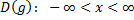 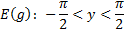 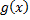 – монотонно возрастает – монотонно возрастает |
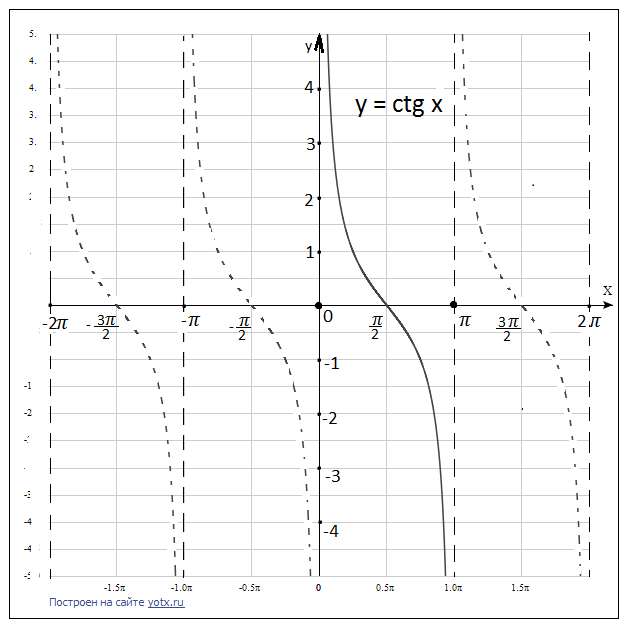 | 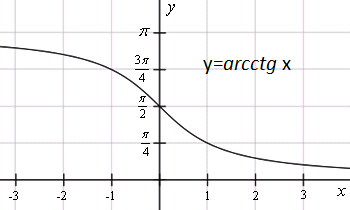 |
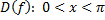 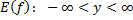 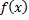 – монотонно убывает – монотонно убывает | 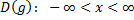 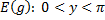 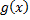 – монотонно убывает – монотонно убывает |
Контрольная работа по теме «Обратная функция»
В. 1
1) Определите ООФ и ОЗФ для обратной функции 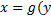 ), если прямая функция
), если прямая функция 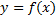 имеет
имеет
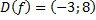 ,
, 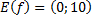 .
.
2) Из уравнения функции 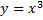 получить уравнение обратной функции.
получить уравнение обратной функции.
3) В системе координат хОу схематично построить функцию 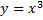 и обратную ей функцию.
и обратную ей функцию.
4) Для построенных функций записать ООФ и ОЗФ.
5) Указать монотонность построенных функций.
