Берілген функцияны фурье Қатарына жіктеу

ТАРАУ

ФУРЬЕ ҚАТАРЫ.

БЕРІЛГЕН ФУНКЦИЯНЫ ФУРЬЕ ҚАТАРЫНА ЖІКТЕУ

4.1. Фурье қатары.Фурье қатары функционалдық қатардың дербес түрі. Функционалдық қатар деп

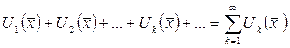
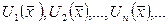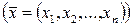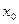түріндегі өрнекті айтады. Мұндағы - бір немесе бірнеше тәуелсіз айнымаларға байланысты функциялар. Ілгеріде біз екі және үш тәуелсіз айнымалыға байланысты функцияларды жиі қолданамыз. Әзірше бір айнымалы функциялардан тұратын қатарларға байланысты негізгі ұғымдарды қарастырамыз. Функционалдық қатар тәуелсіз айнымалысының әрбір бекітіп алынған мәнінде

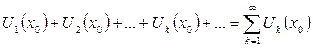
түріндегі сандық қатарға айналады. Сандық қатар жинақталуы да, жинақталмауы да мүмкін. Сандық қатар жинақталса, онда 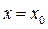нүктесін функционалдық қатардың жинақталу нүктесі деп атайды. Функционалдық қатардың жинақталу нүктелерінен тұратын жиынды қатардың жинақталу облысы деп атайды. Математикалық анализ курсында функционалдық қатардың дербес түрі ретінде

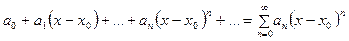
дәрежелік қатары қарастырылады. Оның жинақталу облысы бір 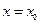нүктесінен, немесе центрі 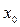нүктесінде орналасқан радиусы 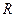– ақырлы санына тең интервалдан, немесе 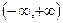аралығындағы барлық нүктелерден тұруы мүмкін. Жалпы жағдайда функционалдық қатардың жинақталу облысын табу қиын есептердің бірі.

Тригонометриялық қатарлар теориясында ортонормаланған функциялар жүйесі қарастырылады. 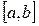кесіндісінде (немесе 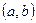интервалында) анықталған және

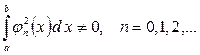
болатын, 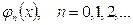функцияларынан құралған 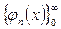жүйесінің мүшелері үшін

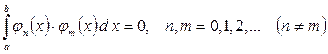
теңдігі орындалатын болса, онда 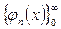жүйесін 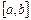кесіндісінде (немесе 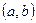интервалында) ортогональ жүйе деп атайды.

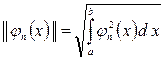
санын 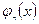функциясының нормасы деп атайды. Егер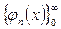 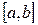кесіндісінде ортогональ жүйедегі 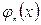функцияларының нормасы бірге тең болса, ондай жүйені ортонормаланған жүйе деп атайды. Ортогональ жүйеге қарапайым мысал ретінде 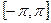аралығында анықталған тригонометриялық функциялардан тұратын

(*)

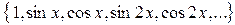жүйесін алуға болады. Осы жүйенің шынында да 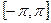кесіндісінде ортогональ жүйе болатындығын көрсету үшін төмендегі интегралдарды есептейік:

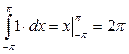
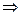
1. 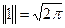; 2.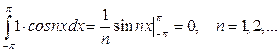

3.

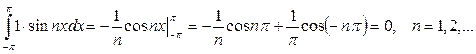
4.

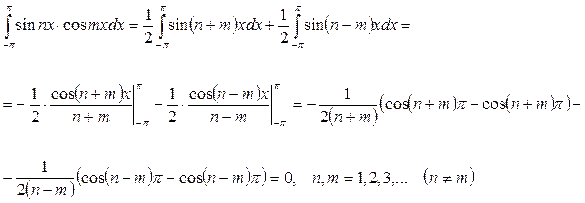
Егер 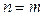болса, онда

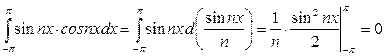
5. 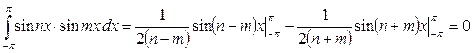, егер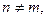 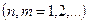болса.

Егер 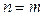болса, онда

.

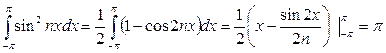Демек,

.

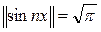6. 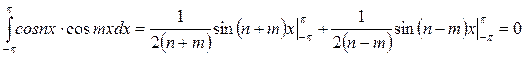, егер

.

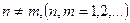Егер 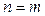болса, онда

.

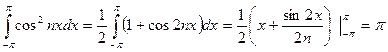Cондықтан,

.

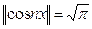Сонымен, (*) жүйесінің 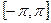кесіндісінде ортогональ жүйе болатындығы дәлелденді. Бірақ ол ортонормаланған жүйе емес. (*) жүйесі ортонормаланған жүйені анықтайды, егер де оған кіретін функциялардың нормасы бірге тең болса, мысалы,

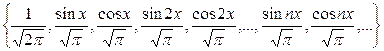
жүйесі 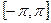кесіндісінде ортонормаланған жүйе. Тағы да ортогональ жүйеге

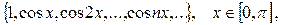
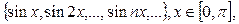
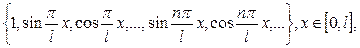
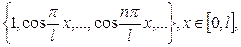
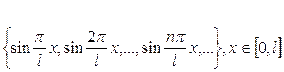
жүйелерін мысал ретінде қарастыруға болады. Тригонометриялық емес те ортогональ жүйелер болады. Оларды ілгерідегі тарауларда қарастыратын боламыз.

4.1.1 анықтама. Коэффициенттері

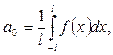
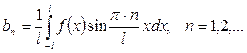(4.1.1)

формулалары арқылы табылатын

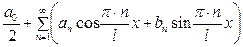
тригонометриялық қатар 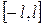аралығында анықталған, периоды 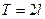тең болатын 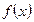функциясының тригонометриялық Фурье қатары деп аталады. Мұндағы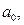 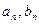. Фурье қатарының коэффициенттері деп аталады.

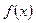функциясының қасиетіне байланысты оған сәйкес келетін тригонометриялық Фурье қатарының түрі өзгеріп отырады. Соған тоқталып өтейік.

1.Егер 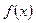функциясының периоды 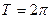болса, онда оған сәйкес келетін тригонометриялық Фурье қатары

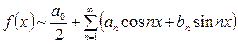
түрінде, ал коэффициенттері

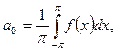
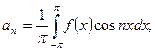
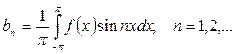
формулалары арқылы табылады.

2.Егер 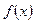функциясы 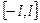аралығында жұп функция болса, онда оған сәйкес келетін тригонометриялық Фурье қатары

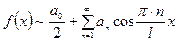
түрінде, ал коэффициенттері

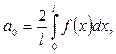
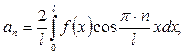
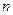=1,2,…

формулалары арқылы табылады.

3.Егер 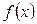функциясы 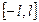аралығында тақ функция болса, онда оған сәйкес келетін тригонометриялық Фурье қатары

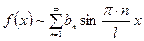
түрінде, ал коэффициенттері

,

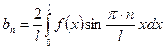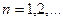
формулалары арқылы табылады.

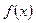функциясына сәйкес келетін тригонометриялық Фурье қатарына байланысты төмендегідей сұрақтар туындайды.

1. 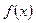функциясына сәйкес келетін тригонометриялық Фурье қатары нүктесінің қандай мәндерінде жинақталады;

2. 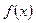функциясына сәйкес келетін тригонометриялық Фурье қатары жинақталса, онда оның қосындысы қай уақытта осы қатарды тудыратын 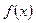функциясына тең болады.Бұл сұрақтарға төменде келтірілетін Дирихле теоремасының тұжырымы жауап береді.

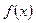функциясы 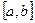аралығында Дирихле шартын қанағаттандырады дейді, егер де ол

а) 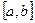кесіндісінде үзіліссіз немесе осы кесіндіде саны ақырлы бірінші ретті үзіліс нүктелерге ие болса;

ә) әрбір үзіліссіз болатын интервалда монотонды немесе осы интервалда саны ақырлы экстремум нүктелерге ие болса.

Мысалы, 13– суретте көрсетілген функция 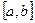кесіндісінде Дирихле шартын қанағаттандырады.

Дирихле теоремасы.Егер периоды 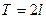тең 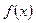функциясы 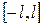кесіндісінде Дирихле шартын қанағаттандыратын болса, онда оны тригонометриялық Фурье қатарына жіктеуге болады, сонымен қатар:

а) 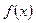функциясы үзіліссіз болатын әрбір нүктесінде тригонометриялық Фурье қатары 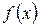мәніне жинақталады;

ә) 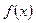функциясы үзілісті болатын әрбір 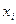нүктесінде тригонометриялық Фурье қатары 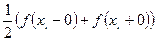мәніне жинақталады. Мұндағы .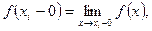

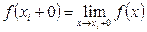13 – сурет.

Ілгеріде дербес туындылы дифференциалдық теңдеулерді шешу кезінде тригонометриялық Фурье қатарын бірнеше рет мүшелеп дифференциалдауға тура келеді. Оған байланысты төмендегідей сұрақтар туындайды:

1) Қандай шарттар орындалғанда, тригонометриялық Фурье қатарының мүшелерінің туындыларынан тұратын қатарлар жинақталады?

2) Қандай жағдайда, осындай қатарлардың қосындылары сәйкесінше берілген функцияның туындыларына тең болады?

Бұл сұрақтарға толық жауап беру біздің курстың аумағынан шығып кетеді. Сонда да айта кететін жағдай, егер 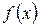функциясының үзіліссіз болуымен қатар қажетті үзіліссіз туындылары бар болса, онда оған сәйкес келетін тригонометриялық Фурье қатарын қажетінше мүшелеп дифференциалдауға болады және одан шыққан қатарлар сәйкесінше берілген функцияның туындыларына жинақталады. Алдағы уақытта тек қана осындай функцияларды қарастыратын боламыз.

Тригонометриялық Фурье қатарын 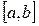кесіндісінде ортогональ болатын функциялар жүйесінен құралған Фурье қатарының дербес жағдайы ретінде қарастыруға болады. Бұл жағдайда жүйеге қатысатын функциялардың периодты болуы міндетті емес.

4.1.2 - анықтама. Коэффициенттері

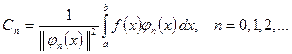
формуласы арқылы табылатын 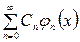қатарын 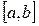кесіндісінде анықталған 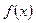функциясының 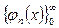ортогональ жүйесі бойынша алынған Фурье қатары деп атайды.

Егер 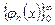ортогональ жүйесі ортонормаланған жүйе болса, онда Фурье қатарының коэффициенттері 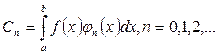формуласы арқылы табылады. Мұндай қатарлардың жинақталуы туралы сұрақтар арнайы ғылыми әдебиеттерде қарастырылады. Біз осы параграфта осындай қатарларға байланысты Стеклов теоремасын келтіреміз.

Стеклов теоремасы. 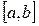кесіндісінде үзіліссіз екінші ретті туындысы бар, 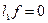және 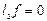біртекті шекаралық шарттарды қанағаттандыратын кез келген 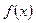функциясы осы кесіндіде 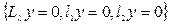- Штурм – Лиувилль есебінің 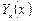өзіндік функциялар жүйесі бойынша жинақталатын Фурье қатарына жіктеледі, яғни 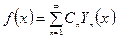. Мұндағы Фурье қатарының коэффициенттері

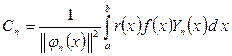
формуласы арқылы табылады.

Қайтадан 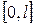кесіндісінде ортогональ жүйе құрайтын

, ;

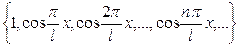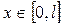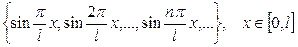
жүйелерін қарастырайық. 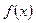– 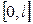кесіндісінде анықталған функция болсын. Онда осы функцияны жоғарыда көрсетілген ортогональ жүйелер арқылы 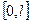кесіндісінде Фурье қатарына жіктеуге болады. Коэффициенттері

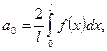
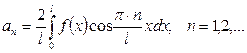
формулалары арқылы табылатын 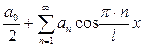тригонометриялық қатарды 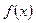функциясының 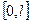кесіндісінде косинустар бойынша Фурье қатары деп атайды. Егер тригонометриялық қатардың 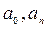коэффициенттері нөлге, ал

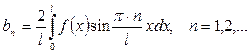
формуласы арқылы табылатын болса, онда

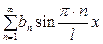
қатарын 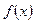функциясының 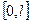кесіндісінде синустар бойынша Фурье қатары деп атайды.

Жоғарыда қарастырылған қатарларды Дирихле теоремасын пайдаланып зерттеуге болады. Нақты айтсақ, егер 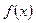функциясы 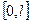кесіндісінде Дирихле шартын қанағаттандыратын болса, онда осы функцияның косинус және синус бойынша Фурье қатарлары жинақталады және 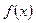функциясының үзіліссіз болатын нүктелерінде берілген қатарлардың қосындысы функцияның осы нүктелердегі мәніне тең болады. 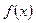функциясының үзіліс нүктелерінде қатарлардың қосындысы осы нүктелердегі функцияның сол және оң жақ шектерінің орта арифметикалық мәніне тең. Кесіндінің шеткі нүктелерінде функцияның косинус бойынша Фурье қатарының қосындысы осы нүктедегі функцияның мәніне, ал синус бойынша Фурье қатарының қосындысы нөлге тең болады.

4.2. Штурм – Лиувилль есебінің өзіндік функциялары арқылы берілген функцияны Фурье қатарына жіктеу.Алдымен Штурм – Лиувилль есебінің өзіндік функциялары тригонометриялық функциялар болатын жағдайларды қарастырайық. Оны мысалдар арқылы түсіндіреміз.

4.2.1 – мысал. 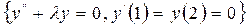- Штурм – Лиувилль есебінің өзіндік функциялары бойынша 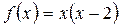функциясын 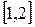кесіндісінде Фурье қатарына жіктеңіз.

Шешу:

1. 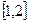кесіндісінде берілген Штурм – Лиувилль есебін тәуелсіз айнымалысына алмастыру жасау арқылы 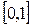кесіндісінде берілетін Штурм – Лиувилль есебіне келтіреміз. Ол үшін 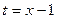деп алмастыру енгіземіз. Онда 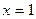болған кезде 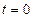және 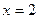болған кезде 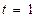болады. Мұндай алмастыру кезінде дифференциалдық теңдеу мен шекаралық шарттар өзгермейді, өйткені

, ;

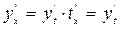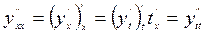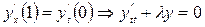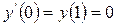, . (4.2.1)

(4.2.1) есебі 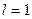болған кезде 3.3 пунктінде қарастырылған (3.3.6) Штурм – Лиувилль есебімен пара – пар болады. Сондықтан (4.2.1) есебінің меншікті мәндері

,

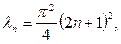
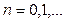ал өзіндік функциялары

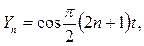
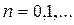
формулалары арқылы табылады.

2. 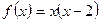функциясы 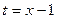алмастыруын қолданғаннан кейін

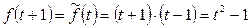
түріне келеді. Бұл функцияны Стеклов теоремасының тұжырымын пайдаланып берілген Штурм – Лиувилль есебінің өзіндік функциялары арқылы жіктейміз, яғни

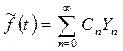
түрінде. Мұндағы

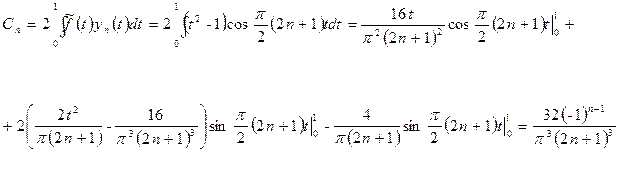
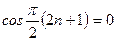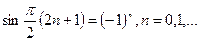(Жоғарыдағы интегралдарды есептеу кезінде және болатындығы ескерілген).

Сондықтан 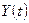функциясына сәйкес келетін тригонометриялық Фурье қатары

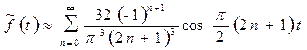
түрінде жазылады.

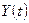функциясы 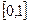кесіндісінде үзіліссіз және Дирихле теоремасының барлық шарттарын қанағаттандыратын болғандықтан

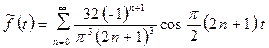(4.2.2)

теңдігі орындалады.

3. 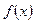функциясын 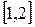кесіндісінде Фурье қатарына жіктеу үшін (4.2.2) теңдігіндегі 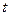айнымалысын 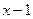айнымалысымен алмастырып,

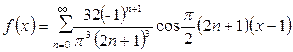
теңдігін аламыз. Бұл теңдік 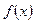функциясының 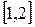кесіндісіндегі берілген Штурм – Лиувилль есебінің өзіндік функциялары бойынша Фурье қатарына жіктеуін анықтайды.

4.2.2 - мысал. 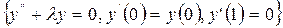- Штурм – Лиувилль есебінің өзіндік функциялары бойынша

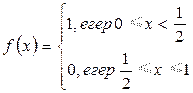
функциясын 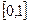кесіндісінде Фурье қатарына жіктеу керек.

1) 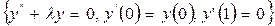- Штурм – Лиувилль есебі 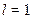болған кезде 3.3 пунктінде қарастырылған (3.3.8) есебімен пара–пар болады. Сондықтан берілген Штурм – Лиувилль есебінің меншікті мәндері 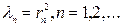( 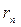сандары 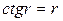теңдеуінің түбірлері), ал өзіндік функциялары

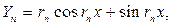
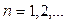
формулалары арқылы табылады.

2) Берілген 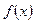функциясын Фурье қатарына жіктейміз:

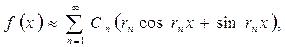
мұндағы

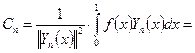
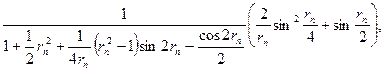
өйткені

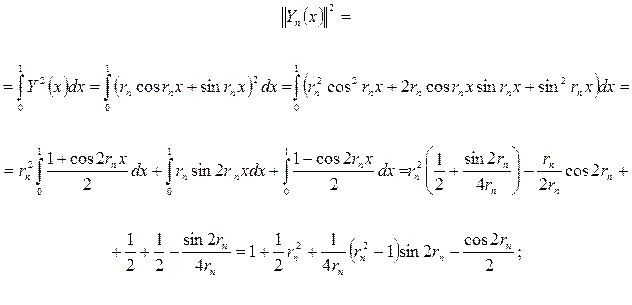
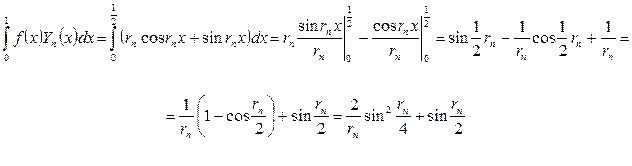
Сондықтан 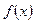функциясына сәйкес келетін тригонометриялық Фурье қатары

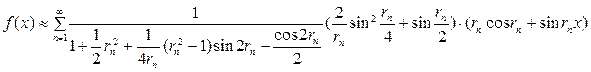
түрінде жазылады. 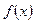функциясы 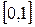кесіндісінде Дирихле шартын қанағаттандыратын болғандықтан, Дирихле теоремасы бойынша

,

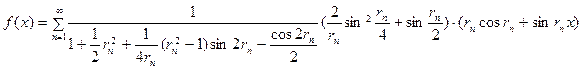егер .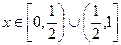

Жоғарыда қарастырылған мысалдарда Штурм-Лиувилль есебінің өзіндік функциялары тригонометриялық функциялар болды. Бірақ, бұдан Штурм-Лиувилль есебінің барлық уақытта өзіндік функциялары тригонометриялық функциялар болады деген тұжырым жасауға болмайды. Соған байланысты мысал қарастырайық.

Мысал.

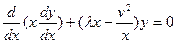(4.2.3)

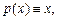
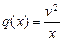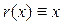
теңдеуін қарастырайық. Мұндағы және функциялары (3.1.5) теңдеуінің коэффициенттерінен айырмашылығы 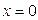болған кезде p(x) пен r(x)нөлге тең болады, ал 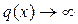, егер 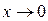. Мұндай жағдайда x=0 нүктесін коэффициенттердің ерекше нүктесі деп атайды. Коэффициенттері ерекше болып келетін жай дифференциалдық теңдеулер дербес туындылы дифференциалдық теңдеулерді шешу кезінде жиі кездеседі. Мысалы, ілгеріде эллиптикалық типті теңдеуге қойылатын Дирихле есебін Фурье әдісімен шешу кезінде біз (4.2.3) теңдеуіне келеміз.

(4.2.3) теңдеуін 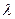және 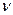параметрлі Бессель теңдеуі деп атайды. Тәуелсіз х айнымалысының орнына жаңа 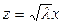айнымалысын енгізу арқылы (4.2.3) теңдеуіндегі 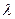параметрінен құтылуға болады, яғни

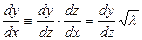
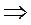
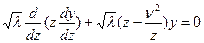
немесе

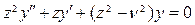(4.2.4)

Бұл жағдайда 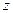айнымалысы комплекс айнымалы болады. (4.2.4.) теңдеуінің шешімдері жалпы жағдайда қарапайым элементар функциялары арқылы өрнектелмейді. Оларды 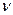- ретті ( 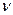- параметрі кез-келген нақты немесе комплекс сандар болуы мүмкін) цилиндрлік немесе Бессель функциялары деп атайды.

(4.2.4) теңдеуінің шешімін

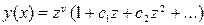
түріндегі жалпыланған дәрежелік қатар түрінде іздестіреміз. Осы қатарды (4.2.4) теңдеуіне қою арқылы қатардың коэффициенттері үшін

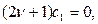
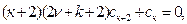
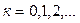(4.2.5)

түрінде анықталатын рекуррентті байланыс аламыз. Осы байланыстарды біртіндеп шешу арқылы

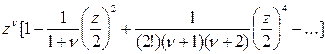(4.2.6)

түріндегі қатарға келеміз. Жақша ішіндегі қатардың х-тің барлық мәндерінде жинақталатындығын көрсету қиын емес. (4.2.6) қатарын 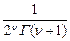өрнегіне көбейтіп, берілген (4.2.4) теңдеуінің шешімі болатын

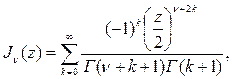
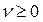(4.2.7)

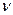-ретті Бессель функциясын аламыз. Мұндағы

,

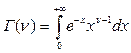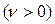
Оны Г- функция деп атайды. Г - функция үшін

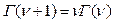
теңдігі орындылады. Осы байланыс Г функциясын 0,-1,-2,... сандардан басқа 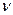параметрінің мәндерінде анықтауға мүмкіншілік береді. Егер 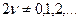болса, онда (4.2.4) теңдеуінің екінші шешімін

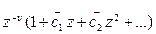
қатар түрінде іздестіруге болады. Бұл жағдайда 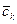- коэффициенттері үшін де (4.2.5) рекурренттік байланысы шығады, тек 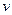-ны (- 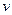)-ға алмастыру керек. Осы байланысты біртіндеп шешу нәтижесінде

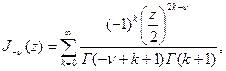
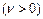
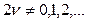
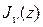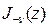түрінде анықталатын екінші шешімге келеміз. және функцияларының сызықты тәуелсіз болатындығы көрініп тұр, өйткені 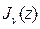функциясы 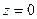нүктесінде нөлге, ал 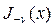функциясы 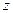нөлге ұмтылған кезде 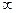-ке ұмтылады. Сондықтан 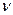- параметрінің жоғарыда көрсетілген мәндерінде

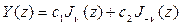
функциясы берілген Бессель теңдеуінің жалпы шешімін анықтайды. Бессель функциясының 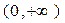аралығында шексіз көп нөлдері болады. Оларды есептеу машиналары арқылы табуға болады немесе олар кейбір әдебиеттерде кесте түрінде беріледі. Бессель теңдеуінің коэффициенттері ерекше болғандықтан 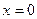нүктесіндегі шекаралық шарт басқаша жаңа нөлге ұмтылған кезде 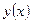шешімі шенелген болу керек деген шартпен алмастырылады. Ал 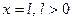нүктесіндегі шарт өзгермейді. Осындай айырмашылықтарға қарамастан Штурм-Лиувилль есебінің өзіндік функциялары мен меншікті мәндерінің қасиеттері Бессель теңдеуі үшін сақталынады. Жоғарыда айтылғандарды тереңірек түсіну үшін 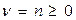бүтін болған кездегі Бессель теңдеуінің дербес түрі

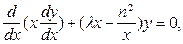
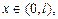
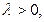
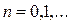(4.2.8)

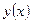-функциясы нөлге ұмтылғанда шенелген

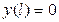(4.2.9)

болатын Штурм-Лиувилль есебін қарастырайық. Жоғарыда көрсетілгендей (4.2.8) теңдеуінің нөлге ұмтылған кезде шенелген болатын 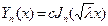( 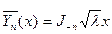шешімі нөлге ұмтылған кезде шенелмеген) шешімі бар. Ол 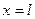нүктесінде

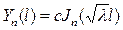
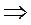
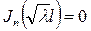(4.2.10)

теңдігін қанағаттандыру керек. (4.2.10) теңдеуінің 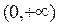интервалында шексіз көп шешімдері бар. Оларды 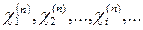түрінде белгілейік. Демек, (4.2.8)-(4.2.9) Штурм-Лиувилль есебінің меншікті мәндері

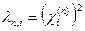, i=1,2,…

ал өзіндік функциялары

,

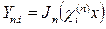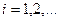
формулалары арқылы табылады.

(4.2.8) )-(4.2.9) Штурм-Лиувилль есебінің меншікті мәндері мен өзіндік функцияларының негізгі қасиеттерін атап өтейік:

1) тек бір 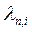меншікті мәніне сәйкес келетін екі өзіндік функция сызықты тәуелді;

2) әр түрлі 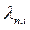және 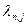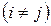меншікті мәндеріне сәйкес келетін екі 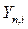және 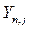өзіндік функциялары 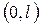интервалында 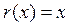салмағы бойынша ортогональ;

3) әртүрлі меншікті мәндерге сәйкес келетін өзіндік функциялар сызықты тәуелсіз функциялар жүйесін құрайды;

4) (4.2.8) )-(4.2.9) есебінің меншікті мәндері нақты сандар;

5) (4.2.8) )-(4.2.9) есебінің

; ,

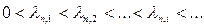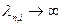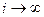
теңсіздігін қанағаттандыратын шексіз көп 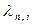меншікті мәндері бар;

Стеклов теоремасының шарттарын қанағаттандыратын 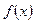функциясының Бессель функциялары арқылы жіктелінген Фурье қатары

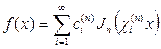
түріндегі теңдікпен беріледі. Мұндағы

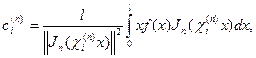
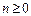
Бессель функциясының нормасын есептеуді арнайы функцияларға арналған кітаптардан табуға болады.

4.3. Кейбір қарапайым тұжырымдар. Ілгеріде қажет болатын математикалық анализде қарастырылатын кейбір қарапайым тұжырымдарды еске түсіріп кетейік.

4.3.1 – лемма. Тақ (жұп) функцияның туындысы жұп (тақ) функция болады.

Дәлелдеуі. 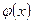функциясы тақ функция болсын, яғни 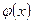функцияның анықталу облысы ноль нүктесіне қарағанда симметриялы жиын және анықталу облысында жатқан кез келген – тер үшін

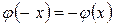(4.3.1)

теңдігі орындалады. (4.3.1) теңдігін дифференциалдау арқылы 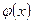анықталу облысында жатқан кез келген – – тер үшін

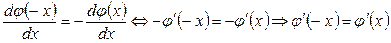(4.3.2)

теңдігін аламыз. Олай болса, 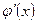жұп функция.

(4.3.2) теңдігін тағы бір рет дифференциалдау арқылы 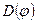анықталу облысында жатқан кез келген –тер үшін

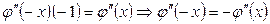
теңдігіне келеміз. Бұдан 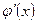жұп функция болған кезде оның туындысы 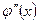- тақ функция болатындығын көреміз.

4.3.2- лемма. Егер 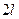периодты тақ 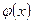функциясының екінші ретті үзіліссіз туындысы бар болса, онда 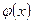функциясы үшін

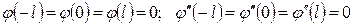
теңдіктері орындалады.

Дәлелдеуі. Лемманың шарты бойынша 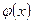– тақ функция. Сондықтан сан түзу бойында жатқан кез келген -тер үшін 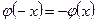теңдігі орындалады. 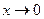кезде соңғы теңдіктен 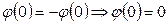теңдігін аламыз. 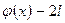периодты функция болғандықтан, .

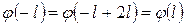Осы теңдікті және 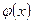тақ функция болатындығын ескеріп,

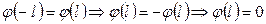
теңдігіне келеміз. Сонымен, .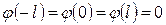

4.3.1-лемманың тұжырымы бойынша тақ функцияның екінші ретті туындысыда тақ функция болатындықтан

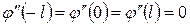
теңдігі орындалатын болады.

4.3.1- теорема. Егер 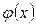( 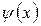) функциясы 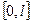кесіндісінде екі рет (бір рет) үзіліссіз дифференциалданатын болса және 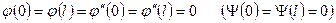шарттын қанағаттандырса, онда оны 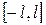аралығында, содан кейін 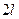– периодты қылып бүкіл сан өсінің бойына жалғастыруға болады. Сонымен қатар, жалғастырудан шыққан функция екі (бір) рет үзіліссіз дифференциалданады және 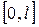кесіндісінде қосындысы 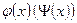функциясына тең болатын синус бойынша Фурье қатарына жіктеледі.

4.3.2 – теорема. Егер 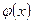функциясының 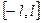кесіндісінде:

а) 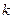рет үзіліссіз туындысы бар болса;

б) 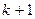-ші ретті туындысы бөлік-үзіліссіз болса;

в) 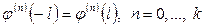болса

онда

,

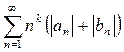қатары жинақталады. Мұндағы 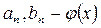функциясының Фурье қатарының коэффициенттері. Сонымен қатар 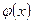функциясының Фурье қатары 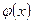функциясына бірқалыпты жинақталады және оны 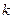-рет мүшелеп дифференциалдауға болады.

Вейерштрасс белгісі. Егер 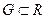облысында анықталған 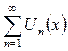функционалдық қатарының 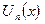жалпы мүшесі 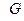облысында жатқан кез келген –тер үшін 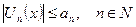теңсіздігін қанағаттандырса және 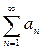сандық қатары жинақталатын болса, онда 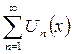функционалдық қатары 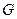облысында бірқалыпты, абсолютті жинақталады және оның қосындысы 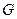облысында үзіліссіз функция болады.

Вейерштрасс белгісі орындалған кезде 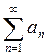сандық қатарын 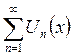функционалдық қатар үшін мажорлаушы (бағалаушы) қатар деп атайды.