Динамика материальной точки и тела, движущегося поступательно 1 страница

МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА

Контрольные задания для студентов всех специальностей

Красноярск

УДК [531+533] (076)

ББК 22.2

Механика и молекулярная физика: Контрольные задания для студентов всех специальностей / КрасГАСА. Красноярск, 2004.

Составили

А. Е. Бурученко

А. А. Колесников

В. А. Захарова

С.С. Лаптев

О.П. Арнольд

Г.Н. Харук

П.П. Машков

Печатается по решению редакционно-издательского совета академии

Ó Красноярская государственная архитектурно-строительная академия, 2004

ВВЕДЕНИЕ

Физика – фундаментальная база для теоретической подготовки инженеров, без овладения которой их успешная деятельность невозможна.

На всех этапах обучения большое значение имеет практическое применение теоретических знаний в процессе решения задач. Это способствует приобщению студентов к самостоятельной творческой работе, учит анализировать изучаемые явления, выделять главные факторы, отвлекаясь от случайных и несущественных деталей.

Задачи, приведенные в методических указаниях, соответствуют программе общего курса физики в техническом вузе и охватывают разделы «Механика», «Колебания и волны», «Молекулярная физика» и «Термодинамика».

В работе отсутствуют сведения, которые при необходимости могут быть найдены в учебных пособиях по курсу общей физики (см. библиографический список). Поэтому вначале помещен краткий перечень формул и законов, необходимых для решения задач.

В приложении приведены основные справочные данные, дополняющие условия задач. Номера вариантов, которые должен выполнить студент, указывает преподаватель.

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

1.1. ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ

Кинематика

Положение материальной точки в пространстве задаётся радиус-вектором :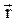

,

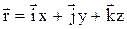где 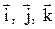– единичные векторы направлений (орты); x, y, z – координаты точки.

Кинематические уравнения движения (в координатной форме) таковы:

; ; ,

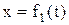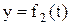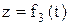где t – время.

Средняя скорость –

< >= ,

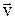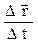где 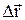– перемещение материальной точки за интервал времени .

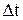Средняя путевая скорость –

< >= ,

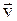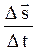где 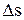- путь, пройденный точкой за интервал времени .

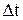Мгновенная скорость –

,

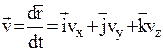где 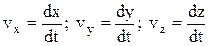– проекции скорости 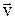на оси координат.

Абсолютное значение скорости –

.

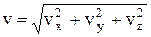Ускорение –

,

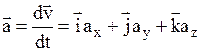где 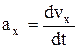; ; 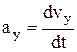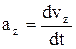– проекции ускорения 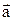на оси координат.

Абсолютное значение ускорения –

.

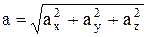При криволинейном движении ускорение можно представить как сумму нормальной 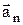и тангенциальной 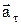составляющих, см. рис 1

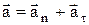
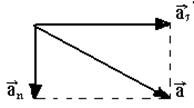Рис. 1.

Абсолютное значение этих ускорений – 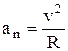; ; 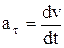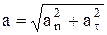, где R – радиус кривизны в данной точке траектории.

Кинематическое уравнение равнопеременного движения материальной точки вдоль оси x:

,

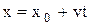где 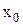- начальная координата; t – время.

При равномерном движении

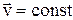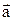; = 0.

Кинематическое уравнение равнопеременного движения (a=const) вдоль оси x :

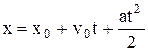
где 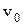– начальная скорость; t – время.

Скорость точки при равномерном движении :

.

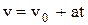Кинематическое уравнение вращательного движения:

.

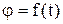Средняя угловая скорость –

,

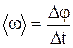где 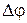- изменение угла поворота за интервал времени .

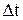Мгновенная угловая скорость –

.

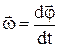Угловое ускорение –

.

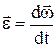Кинематическое уравнение равномерного вращения –

,

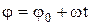где 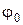- угловое перемещение; t – время. При равномерном вращении

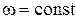и ε=0.

Частота вращения –

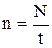, или ,

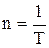где N – число оборотов, совершаемых телом за время t; Т – период вращения (время одного полного оборота).

Кинематическое уравнение равнопеременного вращения (ε=const) :

,

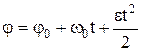где 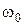- начальная скорость; t – время.

Угловая скорость тела при равнопеременном вращении :

.

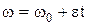Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

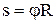(где 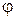– угол поворота тела) – длина пути, пройденного точкой по дуге окружности радиусом R;

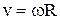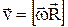, – линейная скорость точки;

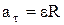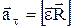, – тангенциальное ускорение точки;

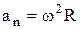– нормальное ускорение точки.

Динамика материальной точки и тела, движущегося поступательно

Уравнение движения материальной точки (второй закон Ньютона)

в векторной форме :

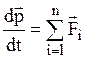, или ,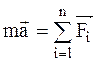

где 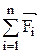- геометрическая сумма сил, действующих на материальную точку; m – масса; 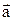– ускорение; 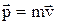– импульс; n – число сил, действующих на точку;

в координатной (скалярной) форме :

; ; ,

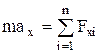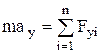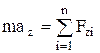или

; ; ,

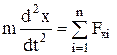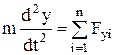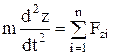где под знаком суммы стоят проекции сил 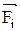на соответствующие оси координат.

Сила упругости –

,

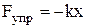где k – коэффициент упругости (в случае пружины жесткости); x – абсолютная деформация.

Сила гравитационного взаимодействия –

,

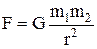где G – гравитационная постоянная; 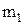и 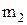- массы взаимодействующих тел, рассматриваемых как материальные точки; r – расстояние между ними.

Сила трения скольжения –

,

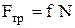где f – коэффициент трения скольжения; N – сила нормального давления.

Значения координат центра масс системы материальных точек –

; ; ,

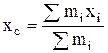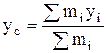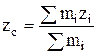где 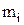– масса 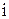- й точки; 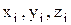– координаты точки.

Закон сохранения импульса –

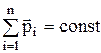, или ,

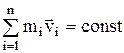где n – число материальных точек или тел, входящих в систему.

Работа, совершаемая постоянной силой, –

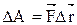, или ,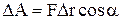

где 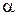– угол между направлениями векторов силы 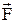и перемещения .

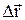Работа, совершаемая переменной силой, –

,

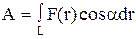причем интегрирование ведётся вдоль траектории, обозначаемой L.

Средняя мощность за интервал времени –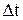

.

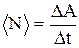Мгновенная мощность –

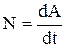, или ,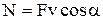

где dA – работа, совершаемая за промежуток времени dt.

Кинетическая энергия материальной точки (или тела, движущегося посту­пательно) –

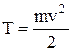, или .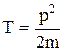

Соотношение потенциальной энергии тела и силы, действующей на него в данной точке поля, –

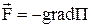, или ,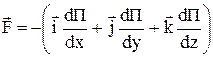

где 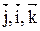– единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (например, гравитационное), –

.

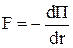Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины) –

.

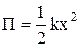Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массам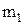и и 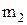, находящихся на некотором расстоянии друг от друга,-

.

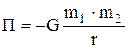Потенциальная энергия тела, находящегося в однородном поле силы тяжести, –

,

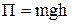где h – высота нахождения тела над уровнем, принятым за нулевой для отсчёта потенциальной энергии. Эта формула справедлива при условии, что h<<R, где R – радиус Земли.

Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде

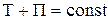
Применив законы сохранения энергии и импульса в случае прямого центрального удара шаров, получаем формулу скорости абсолютно неупругих шаров

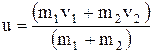
и формулы скорости абсолютно упругих шаров после удара:

,

,

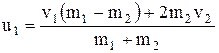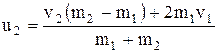где 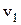и 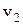– скорости шаров до удара; 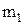и 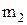– их массы.

Механика твёрдого тела

Основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси –

,

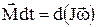где 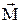– момент силы, действующей на тело в течение времени dt; J – момент инерции тела; 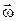– угловая скорость; J 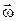– момент импульса.

Если момент силы и момент инерции постоянны, то это уравнение записывается в виде

.

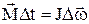В случае постоянного момента инерции

,

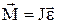где 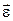- угловое ускорение.

Момент силы 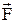, действующей на тело, относительно оси вращения –

,

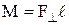где 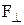– проекция силы 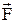на плоскость, перпендикулярную оси вращения; 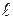– плечо силы (кратчайшее расстояние от оси вращения до линии действия силы).

Момент инерции материальной точки –

,

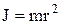где m – масса точки; r – расстояние от оси вращения до точки.

Моменты инерций некоторых тел правильной геометрической формы приведены в табл. 1.

Таблица 1

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой m и длиной	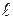Проходит через центр тяжести стержня перпендикулярно ему Проходит через конец стержня перпендикулярно ему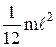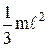
Тонкое кольцо, обруч, труба радиусом R и массой m, распределённой по ободу	Проходит через центр кольца, обруча, трубы, маховика перпендикулярно плоскости основаня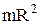
Круглый однородный диск (цилиндр) радиусом R и массой m	Проходит через центр диска перпендикулярно его плоскости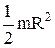
Однородный шар массой m и радиусом R	Проходит через центр шара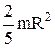

Момент инерции твёрдого тела –

,

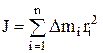где r_i – расстояние от элемента массы Dm_i до оси вращения.

В интегральной форме это выглядит так :

.

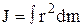Если тело однородно, т. е. его плотность ρ одинаково по всему объёму, то

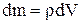и ,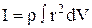

где V – объём тела.

Теорема Штейнера. Момент инерции тела относительно произвольной оси равен

,

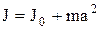где 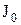– момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; m – масса тела; a – расстояние между осями.

Закон сохранения момента импульса –

,

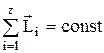где 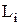- момент импульса тела под номером i, входящего в состав системы.

Закон сохранения момента импульса для двух взаимодействующих тел –

,

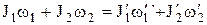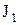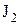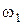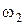где , , и - моменты инерции и угловые скорости тел до взаимодействия; 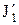, , 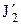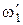и 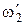- те же величины после него.

Закон сохранения момента импульса для одного тела, момент инерции которого меняется, –

,

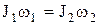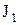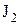где и – начальный и конечный моменты инерци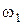и; и 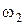– начальная и конечная угловые скорости тела.

Работа постоянного момента силы M, действующего на вращающееся тело, –

,

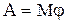где φ – угол поворота тела.

Мгновенная мощность, развиваемая при вращении тела –

.

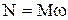Кинетическая энергия вращающегося тела –

.

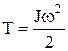Кинетическая энергия тела, катящегося по плоскости без скольжения, –

,

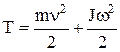где 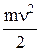– кинетическая энергия поступательного движения тела; 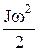– кинетическая энергия вращательного движения вокруг оси, проходящей через центр инерции.

Работа, совершаемая при вращении тела, и изменение его кинетической энергии связаны соотношением

.

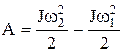Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения (см. табл. 2).

Таблица 2

Поступательное движение	Вращательное движение	Поступательное движение	Вращательное движение
Основной закон динамики	Работа и мощность
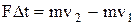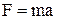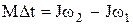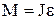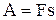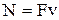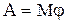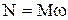Закон сохранения	Кинетическая энергия
импульса	момента импульса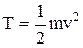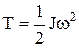

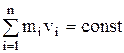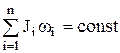Относительное продольное растяжение (сжатие) :

,

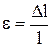где 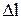– изменение длины тела при растяжении (сжатии); l – длина тела до деформации.

Относительное поперечное растяжение (сжатие) :

,

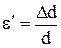где 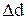– изменение диаметра стержня при растяжении (сжатии); d – диаметр стержня.

Связь между относительным поперечным (растяжением) сжатием 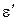и относительным продольным растяжением (сжатием) ε –

,

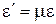где µ – коэффициент Пуассона.

Закон Гука для продольного растяжения (сжатия) :

,

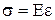где Е – модуль Юнга.

Напряжение упругой деформации –

,

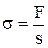где F – растягивающая (сжимающая) сила; s – площадь поперечного сечения.

Потенциальная энергия упругорастянутого (сжатого) стержня –

,

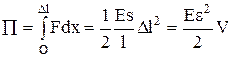где V – объём тела.

Механические колебания

Уравнение гармонических колебаний –

,

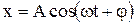где x – смещение колеблющейся точки от положения равновесия; A, ω, φ – соответственно амплитуда, круговая (циклическая) частота, начальная фаза колебаний; t – время; 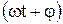– фаза колебаний в момент t.

Круговая частота колебаний –

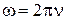, или ,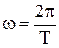

где n и T – частота и период колебаний.

Скорость точки, совершающей гармонические колебания, –

.
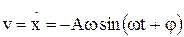