Общая классификация моделей

В основе моделирования лежит теория подобия, согласно которой абсолютное подобие может иметь место лишь при замене одного объекта другим, точно таким же. При моделировании невозможно добиться абсолютного подобия и нужно стремиться к тому, чтобы модель достаточно хорошо отражала исследуемую сторону функционирования объекта (например, процессы восстановления или осаждения металла). Поэтому в качестве одного из признаков классификации видов моделирования можно выбрать степень полноты модели и разделить модели в соответствии с этим признаком на полные, неполные и приближенные.

В основе полного моделирования лежит полное подобие, которое проявляется как во времени, так и в пространстве. Для неполного моделирования характерно неполное подобие модели изучаемому объекту «горячая» модель электролизера). Приближенное моделирование опирается на приближенное подобие, при котором отдельные стороны функционирования реального объекта не моделируются совсем («холодная» модель электролизера).

В зависимости от характера изучаемых процессов в системе все виды моделирования могут быть сведены в схему, представленную на рис. 2.1.

Детерминированное моделирование отображает детерминированные процессы (т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий); стохастическое моделирование – вероятностные процессы и события. Статическое моделирование служит для описания поведения объекта в какой-либо момент времени (в статике). Динамическое моделирование отражает закон изменения состояния объекта во времени.

Дискретное моделирование служит для описания дискретных процессов. Непрерывное моделирование позволяет отразить непрерывные во времени процессы. Дискретно-непрерывное моделирование используют, когда необходимо выделить наличие как дискретных, так и непрерывных процессов (непрерывный процесс плавки и периодический выпуск продуктов плавки).

Линейное моделирование применяют для описания линейных процессов, т.е. процессов, связь между входными и выходными параметрами которых линейна. Нелинейное моделирование предназначено для описания нелинейных процессов, в которых связь между выходом и входом системы нелинейна.В зависимости от формы представления объекта можно выделить мысленное и реальное моделирование. При реальном моделировании используется возможность исследования характеристик либо на реальном объекте, либо на его части. Оно подразделяется на натурное и физическое.

Натурное моделирование подразделяют на научный эксперимент, комплексные испытания и производственный эксперимент, реализованные на основе теории подобия и обладающие высокой достоверностью.

Физическое моделирование отличается от натурного тем, что исследования проводятся на установках, которые сохраняют природу явления и обладают физическим подобием в реальном и нереальном масштабе времени (моделирование процесса электролиза).

Мысленное моделирование часто является единственным способом моделирования объектов, которые либо нельзя реализовать в заданном интервале времени, либо существуют вне условий, возможных для их физического воссоздания. Оно может быть наглядным, символическим и математическим. При наглядном моделировании создаются наглядные модели, которые отображают явления и процессы, протекающие в объекте. Наглядное моделирование подразделяется на гипотетическое (в основе гипотезы), аналоговое (аналогии различных уровней) и макетирование (мысленный макет). Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает его основные свойства (электрические схемы, чертежи, карты и т.д.). Под математическим моделированием понимают процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать численные характеристики рассматриваемого реального объекта. Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.

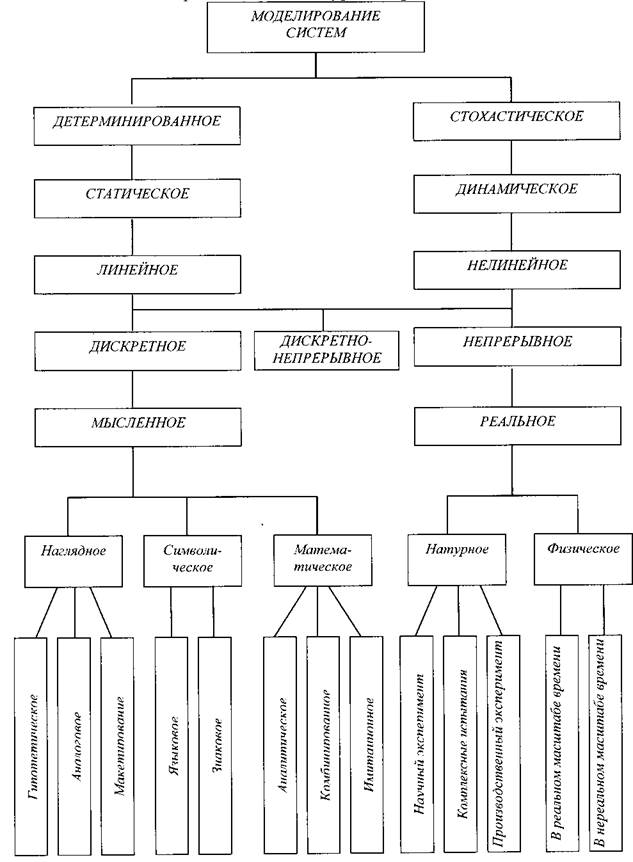
Рис. 2.1. Классификация моделей

Для аналитического моделирования характерно то, что процесс функционирования элементов системы (физико-химические превращения, загрузка, выпуск, тепло- и массоперенос) описывается в виде некоторых функциональных соотношений (алгебраических, дифференциальных, конечно-разностных) или логических условий. Аналитическая модель может быть исследована различными методами:

♦ аналитическим, когда искомые характеристики пытаются найти в общем виде;

♦ численным, когда, не зная решения в общем виде, стремятся получить числовые результаты при конкретных начальных условиях;

♦ качественным, когда, не имея решения в явном виде, можно установить некоторые его свойства по самой модели (изменение заглубления электродов приводит к изменению токораспределения по объему ванны РТП).

Аналитический метод широко применяется для простых систем, с усложнением систем использование этого метода возможно при упрощении первоначальной модели. Численный метод по сравнению с аналитическим позволяет исследовать более широкий класс систем, но при этом полученные решения носят частный характер (процесс обжига при известном химическом составе шихты). Численный метод особенно эффективен при использовании ЭВМ.

При имитационном моделировании имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени. Основным преимуществом имитационного моделирования перед аналитическим является возможность решения более сложных задач. Имитационные модели позволяют относительно просто учитывать следующие факторы: наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия.

Для построения имитационной модели используют машинные реализации случайных величин и функций, полученные методом статистического моделирования (Монте-Карло). Данный метод применяется для численного решения аналитической задачи. Особенно эффективны статистические методы при неполной информации о процессе.

Комбинированное моделирование позволяет объединить достоинства аналитического и имитационного моделирования. При этом часть подсистем описывается аналитическими моделями, а часть – имитационными.

Модели математического программирования являются классом моде-лей, применяемых для решения оптимизационных задач.

В самом общем случае задачи математического программирования

имеют следующий вид: найти точки максимума функции

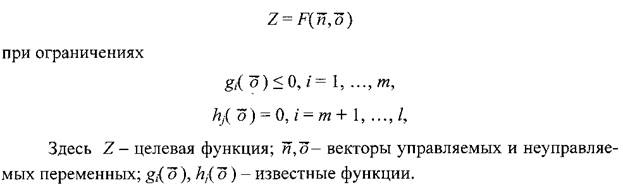
Для нахождения решения данной задачи в зависимости от вида структуры целевой функции и ограничений используют:

♦ методы линейного программирования, если F(c, x), g_i(x), h_j(x) линейны относительно переменных x;

♦ методы нелинейного программирования, если F(c, x), g_i(x), h_j(x) не-линейны относительно переменных x;

♦ методы динамического программирования, если F(c, x) имеет специальную структуру;

♦ методы стохастического программирования, когда вектор неуправляемых переменных x случаен;

♦ сетевые модели (позволяют отобразить объем практических взаимообусловленных работ, последовательность их выполнения, а также логическую взаимосвязь);

♦ модели массового обслуживания (для решения задач обслуживания массового потребителя).