Движение заряженных частиц в магнитном поле

Эффект Холла

Если движется одиночный заряд q то он создаёт электрический ток, а следовательно и магнитное поле.

По закону БСЛ: 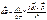, если скорость заряда , то

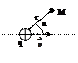тогда: 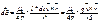(т.к. I*dt = q)

В скалярной форме: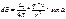

т.к. движущийся заряд это ток то на него со стороны магнитного поля на него будет действовать сала, аналогичная силе Ампера: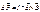

Но 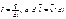подставим и получим: 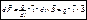- это силу называют силой Лоренса.

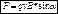- сила Лоренца в скалярном виде.

Направление силы Лоренца определяется по правилу левой руки (для положительного заряда).

Под действием силы Лоренца проводники движутся по окружности.

В любой точке какой бы не взяли сила Лоренца направлена к центру.

Найдём радиус окружности F=ma, F=qvB (sinᾳ=1) a = v²/R

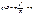
Эффект Холла

Поместим метал или полупроводник с током в магнитное поле. На движущиеся электроны будет действовать сила Лоренса. Она отклонит электроны к одной стороне проводника создав разность потенциалов. В условии равновесия сила Лоренца равна силе Кулоновской. F_л = F_кул.

evB = eE. Заменим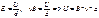

U – разность потенциалов, d – толщина проводника.

Виток с током в магнитном поле.

Момент сил, действующий на виток

С током в магнитном поле. Магнитный момент.

Контур с током в магнитном поле.

Поместим квадратный контур с током в магнитное поле. Силы F_в уравновешивают друг друга. Силы F_А поворачивают контур.

Сила F_а равна: F_а = I*B*a

Момент этих сил равен:

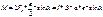
Величина а*в = S – площадь контура.

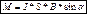
Величина I*S = P_m – называется магнитным моментом.

Тогда: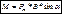

Теорема о циркуляции вектора магнитной

Индукции для магнитного поля в вакууме.

Магнитного поля соленоида и тороида.

Аналогично циркуляции вектора 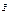, можно: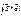

Вводят циркуляцию вектора :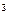

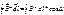
Пусть магнитное поле создано проводником с током I.

Вычислим циркуляцию вектора 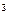по контуру являющемуся окружностью в центре которой находится проводник.

Циркуляция равна: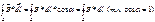

Индукция B равна: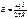

Подставим: 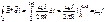- эта формула верна для любого замкнутого контура и любого числа проводников.

Теорема о циркуляции или закон полного тока.

Циркуляция вектора 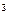по любому замкнутому контуру равна сумме токов внутри этого контура умноженного на μ₀: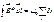

Магнитное поле соленоида.

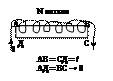Соленоид – цилиндрическая однослойная катушка у которой длина l значительно больше диаметра. Внутри соленоида магнитное поле однородное вне очень слабое.

Возьмём прямоугольный контур АВСД.

(АВ внутри, а СД снаружи лежат)

По закону полного тока: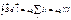

Рассмотрим левую часть контура:

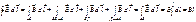
следовательно:Bl=μ₀*N*I =>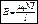

Магнитное поле второида

Индукцию внутри тороида можно найти по той же формуле что и соленоида, если считать, что: l = 2πR.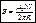

Магнитный поток.