Требования к выполнению контрольных работ

Введение.

Математика относится к предметам естественно-научного блока и для специальности «Сварочное производство» является общеобразовательной дисциплиной. Развитие современных технологий и усложнение производственных процессов требует от специалистов более высокого уровня квалификации. В частности, необходимо получение математического образования, носящего при изучении общепрофесиональных и специальных дисциплин прикладной характер. На математических методах основываются такие дисциплины как «Метрология, стандартизация и сертификация», «Нормирование» и другие. Поэтому целью студентов при изучении дисциплины «Математика» является получение представления о роли и месте математических методов в современном мире, изучение понятий, носящих прикладной характер, которые модно использовать при изучении специальных дисциплин.

Изучение математики предусматривает:

ü Развитие логического мышления;

ü Овладение основными методами исследования и решения математических задач;

ü Формирование умения самостоятельно расширять математические знания и проводить анализ прикладных задач.

В данных методических рекомендациях приводится содержание дисциплины «Математика», где указаны основные разделы и темы изучаемого курса. Теоретическая часть каждого раздела представлена перечислением основных понятий. Большинство этих понятий изучается студентами заочной формы обучения самостоятельно, а также с помощью аудиторных часов и консультаций преподавателя.

В процессе изучения дисциплины студенты выполняют две контрольных работы. Контрольная работа №1 включает в себя два раздела: основы линейной алгебры и основы математического анализа. Контрольная работа №2 включает следующие разделы: основы теории вероятностей и математической статистики,

основы дискретной математики, последовательности и ряды

Содержание дисциплины.

1. Основы линейной алгебры.

Понятие определителя 2-ог и 3-его порядка. Правило треугольников для вычисления определителя. Матрица. Квадратная матрица 2-го и 3-его порядка. Нулевая матрица. Единичная матрица. Матрица-столбец. Алгебраическое дополнение элемента матрицы.

Системы m линейных уравнений с n неизвестными. Матрица и расширенная матрица системы уравнений. Формулы Крамера и метод Гаусса для решения системы линейных уравнений.

2. Основы математического анализа.

Понятие предела функции в точке. Свойства предела функции. Односторонние пределы. Непрерывные функции, их свойства. Точки разрыва, их классификация. Замечательные пределы.

Определение производной функции. Правила дифференцирования. Производная сложной функции. Таблица производных. Вторая производная. Асимптоты графика функции. Направления выпуклости графика функции. Общая схема исследования функции.

Понятие неопределенного и определенного интеграла. Свойства интегралов. Таблица интегралов. Методы вычисления интегралов (непосредственное интегрирование, введение новой переменной, интегрирование по частям).

3. Основы теории вероятностей.

Классическое определение вероятности. Вычисление вероятности в простейших случаях. Теоремы сложения и умножения вероятностей несовместных событий. Случайные величины. Дискретная случайная величина. Закон распределения дискретной случайной величины. Математическое ожидание, дисперсия, функция распределения случайной величины.

4. Основы дискретной математики.

Множество, упорядоченное множество, подмножество. Отношение, свойства отношений. Операции с множествами: объединение, пересечение. Основные понятия теории графов.

5. Последовательности и ряды.

Определение числового ряда. Признаки сходимости ряда. Знакочередующиеся ряды. Функциональные последовательности и ряды. Степенные ряды.

Требования к выполнению контрольных работ.

Контрольная работа должна быть выполнена в отдельной тетради (или двойных тетрадных листах в клеточку, сложенных в виде тетради), где необходимо оформить титульный лист.

1. Титульный лист должен содержать фамилию, имя, отчество студента, номер контрольной работы, специальность, номер учебной группы (образец оформления в приложении 1).

2. При выполнении контрольной работы условие каждой задачи должно быть переписано в тетрадь. При решении заданий все приводимые вычисления и ответы на вопросы должны быть четкими, конкретными, соответствовать условию задачи, должны быть приведены подробные обоснования приведенного решения.

3. Все решения следует располагать в порядке номеров задач.

4. Для студентов заочной формы обучения работа должна быть сдана не позднее, чем в первый день сессии.

5. Номер варианта определяется по последней цифре зачетной книжки. (Например: последняя цифра зачетной книжки 7 соответствует варианту 7, цифра 0 соответствует варианту 10)

Контрольная работа № 1

Вариант 1.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

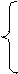2х₁ + х₂ – 3х₃ = - 9

х₁– х₂ – х₃ = - 4

5х₁+ 2х₂ + х₃ = 11

2. Вычислить пределы:

а) lim x² – 25 ^{x→ 5} x – 5

б) lim 2x²– 3x +4 ^x→∞ 7x²+ 2x - 1

в) lim sin2x ^{x→ 0} tg7x

3. Найти производную:

а) у = 2х⁵+6х²- 4х–2; б) y = x² tgx; в) у = (х²+2)/(х-1); г) y = sin (5x² +2x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 3x² – х³ + 2

5. Найти неопределенный интеграл:

а) ò (2х³-5х²+7х)dx

б) ò (2x +8)¹¹dx

в) ò x sin4x dx

6. Вычислить определенный интеграл:

₃

∫(x²-x)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х², у = 2 – х, у = 0

8. Найти общее и частное решение дифференциального уравнения, при заданных начальных условиях:

(4 + 7х)·у' = 7у , у(0) = 1

Вариант 2.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

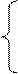3х₁ – 2х₂ + 4х₃ = 8

х₁+ 5х₂ – х₃ = 7

2х₁+ 2х₂ – х₃ = 1

2. Вычислить пределы:

а) lim x² – 16 ^{x→ 4} x – 4

б) lim 2x³– 3x +1 ^x→∞ 5x³+ 4x – 1

в) lim sin3x ^{x→ 0}tgx

3. Найти производную:

а) у=4х³+2х²+8х–12; б) у = sin x ln x; в) у = (х³+7)/(х-2); г) y = cos(x³ – 7x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 2х³+ 3х² – 1

5. Найти неопределенный интеграл:

А) ò (4х³-9х²+7х)dx

Б) ò (2x +1)²⁴dx

В) ò x cosx dx

6. Вычислить определенный интеграл:

₃

∫(x²-x)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х², у = 2 – х

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(7 + 3х)·у' = 2у , у(0) = 1

Вариант 3.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

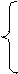10х₁ - х₂ – х₃ = 47

5 х₁+ х₂ + 2х₃ = 30

х₁+ 4х₂ – 3х₃ = 3

2. Вычислить пределы:

А) lim 3x² – 2x ^{x→ 0} 5x

Б) lim 3x⁵– 4x – 7 ^x→∞ 7x⁵- 3x + 2

В) lim tg2x ^{x→ 0}tg4x

3. Найти производную:

а) у=3х⁷- 6х³+ 7х–5; б) у = e^x sin x в) у = (х²+1)/(х – 4) г) y = tg (2x² + 3x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 3х² – 2х³ + 3

5. Найти неопределенный интеграл:

А) ò (2х³+3х²+х)dx

Б) ò (5x +8)¹⁰dx

В) ò x e^x dx

6. Вычислить определенный интеграл:

₄

∫(3x²+x)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х²: у = 1

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(5 + 4х)·у' = 8у, у(0) = 1

Вариант 4.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

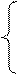Требования к выполнению контрольных работ - student2.ru - х₁ + 3х₂ + 2х₃ = 6

2х₁+ х₂ + 5х₃ = 11

2х₁+ 5х₂ – 3х₃ = 11

2. Вычислить пределы:

А) lim x² – 9 ^{x→ -3} x + 3

Б) lim 7x⁴– 3x +5 ^x→∞ 2x⁴ - 6x +3

В) lim sin2x ^{x→ 0}3х

3. Найти производную:

а) у = 7х⁴+2х³- 4х+10; б) у = x² ctg x; в) у = (х² – 5)/(х+7); г) y = ln (x⁴ – 2x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = х³ – 12х +2

5. Найти неопределенный интеграл:

А) ò (2х⁵-5х⁴+7)dx

Б) ò (2x +8)¹¹dx

В) ò x arctgx dx

6. Вычислить определенный интеграл:

₃

∫(x²+2)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х²; у = х + 2

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(8 + 6х)·у' = 6у, у(0) = 2

Вариант 5.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

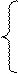2х₁ + 3х₂ + 3х₃ = 13

- х₁+ 4х₂ – х₃ = - 5

4х₁+ х₂ – 3х₃ = - 1

2. Вычислить пределы:

А) lim x – 5 ^{x→ 5} x² – 25

Б) lim 4x³– 5x² - 7 ^x→∞ 5x³+ 2x – 2

В) lim tg5x ^{x→ 0}sin2x

3. Найти производную:

а) у=5х⁵+х²+8х–22; б) y = √x sin x; в) у = (х²+3)/(х-5); г) y = (6x² + 3x)⁶

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 3х – х³ – 3

5. Найти неопределенный интеграл:

А) ò (х³-х⁶+8х)dx

Б) ò sin(2x +3)dx

В) ò x sin2x dx

6. Вычислить определенный интеграл:

₃

∫(3x²+2x)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х²; у = 4

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(3 + 4х)·у' = 8у, у(1) = 0

Вариант 6.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

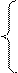5х₁ – 2х₂ – х₃ = 2

3х₁+ 4х₂ – 5х₃ = 4

х₁+ 3х₂ – 2х₃ = - 1

2. Вычислить пределы:

А) lim x² – 49 ^x→⁷ x – 7

Б) lim 2x²– x +8 ^x→∞ 3x²- 2x +7

В) lim sin6x ^{x→ 0}tg8x

3. Найти производную:

а) у=2х⁹+6х⁴– х + 16; б) y = cos x lnx; в) у = (х²+1)/(х²-1); г) y = cos (x⁴ – 2x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = х³/3 – х² – 3х

5. Найти неопределенный интеграл:

А) ò (7х³-5х+4)dx

Б) cos(2x -5)dx

В) ò x cos3x dx

6. Вычислить определенный интеграл:

₄

∫(x²-x)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х²; у = х

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(3 – 5х)·у' = 5у, у(1) = 3

Вариант 7.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

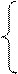Требования к выполнению контрольных работ - student2.ru 2х₁ – 3х₂ + 2х₃ = 2

х₁+ 2х₂ – х₃ = 2

3х₁+ х₂ + х₃ = 8

2. Вычислить пределы:

А) lim x²–121 ^x→^-11x + 11

Б) lim 6x²+x + 12 ^x→∞ x²+ 5x – 8

В) lim ctg2x ^{x→ 0}sin7x

3. Найти производную:

а) у=х⁵+5х²+ 12х–2; б) y = 2x e^x; в) у = (х³+1)/(х³-1); г) y = (5x² +2x)⁷

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = х⁴ – 2х² – 3

5. Найти неопределенный интеграл:

А) ò (3х⁵-5х²- х)dx

Б) ò sin(8x -1)dx

В) ò e^2x x dx

6. Вычислить определенный интеграл:

₃

∫(x²-x)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = 4 – х²; у = 3

8.Найти общее и частное решение дифференциального уравнения: при заданных начальных условиях:

(6 – 3х)·у' = 3у, у(0) = 2

Вариант 8.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

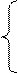Требования к выполнению контрольных работ - student2.ru 2х₁ – х₂ + х₃ = 0

х₁+ х₂ – 2х₃ = - 5

х₂ – 4х₃ = - 8

2. Вычислить пределы:

А) lim 5x²–25х ^{x→ 5} x – 5

Б) lim 8x⁶– 6x⁴ ^x→∞ 6x⁶-5x² - 1

В) lim хsin2x ^{x→ 0}tgx

3. Найти производную:

а) у=3х⁵- 2х⁴- 4х–44; б) y = e^x cos x; в) у = (х²+3)/(х²-3); г) y = sin (2x² + 3x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 4х² – х⁴ + 1

5. Найти неопределенный интеграл:

А) ò (х³-8х²+5)dx

Б) ò sin(5x -3)dx

В) ò x sinx dx

6. Вычислить определенный интеграл:

₂

∫(3x²+x)dx

⁰

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х; у = 2 – х; у = 0

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(9 – 2х) · у' = 4у, у (0) = 3

Вариант 9.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

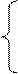2х₁ + х₂ – х₃ = 5

х₁– 2х₂ + 3х₃ = - 3

7х₁+ х₂ – х₃ = 10

2. Вычислить пределы:

А) lim x + 4 ^x→^-4 x² – 16

Б) lim 10x²– 9x+2 ^x→∞9x²+ 12x

В) lim sin8x ^{x→ 0}хtg4x

3. Найти производную:

а) у=1/8х⁸+х⁵+3х–21; б) y = x³ ln x; в) у = (х²-5)/(х²+5); г) y = (x³ – 7x)⁹

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 3х⁵ – 5х³ – 1

5. Найти неопределенный интеграл:

А) ò (8х³-х⁵+9х)dx

Б) ò (6x -7)⁶dx

В) ò x cosx dx

6. Вычислить определенный интеграл:

₄

∫(x²+2)dx

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х²+ 2, у = х + 4

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(10 + 3х) · у' = 3у, у(0) = 1

Вариант 10.

1. Решить систему уравнений: а) методом Крамера; б) методом Гаусса

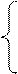2х₁ + 4х₂ + х₃ = 4

3х₁+ 6х₂ + 2х₃ = 4

4х₁– х₂ – 3х₃ = 1

2. Вычислить пределы:

А) lim x² – 81 ^{x→ 9} x – 9

Б) lim 2x⁷– 3x ⁴ ^x→∞ 7x⁷+ 2x⁵

В) lim ctgx ^{x→ 0}sin5x

3. Найти производную:

А) у=1/5х⁵+1/2х²–х+1; Б) y = 4x² cos x;

В) у = (х²+2х)/(х²-1); Г) y = sin (2x² + 3x)

4. Исследовать методами дифференциального исчисления функцию и построить ее график:

y = 4х⁵ – 5х⁴

5. Найти неопределенный интеграл:

А) ò (2х – 5х⁴+12)dx

Б) ò (2 +8x)²¹dx

В) ò x e^3x dx

6. Вычислить определенный интеграл:

₄

∫(3x²+2x)dx

⁰

7. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.

у = х²+ 1, у = 2

8. Найти общее и частное решение дифференциального уравнения при заданных начальных условиях:

(4 + 3х) · у' = 3у, у(0) = 1

Контрольная работа №2.

Вариант 1.

1. Решить задачи:

1) Студент знает ответ на 20 вопросов из 25. Какова вероятность, что он знает ответ на два из предложенных ему трех вопросов?

2) Три стрелка стреляют по мишени. Вероятность попадания первого – 0,6, второго – 0,7, третьего 0,8. Найти вероятность того, что при одном залпе обнаружится не менее двух попаданий?

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,3	0,3	Р₃

Найти: а) р₃ ; б) математическое ожидание величины; в) дисперсию; г) среднее квадратическое отклонение, д) функцию распределения; е) построить полигон распределения.

2. Исследовать ряд на сходимость:

_∞

∑ n

ⁿ⁼¹2ⁿ

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, -7< x £ 9}; B = {2x: x ÎN, -1< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств.

Вариант 2.

1. Решить задачи:

1) Студент знает ответ на 25 вопросов из 30. Какова вероятность, что он знает ответ на два из предложенных ему трех вопросов?

2). Три стрелка стреляют по мишени. Вероятность попадания первого – 0,7 второго – 0,7, третьего 0,8. Найти вероятность того, что при одном залпе обнаружится ровно два попадания?

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,4	0,2	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ n

ⁿ⁼¹ 3ⁿ⁺¹

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, -5< x £ 10}; B = {3x: x ÎN, -1< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 3.

1. Решить задачи:

1) Вини Пух берет с полки горшочки с медом и пустые возвращает обратно, чтобы не портить внешний вид. У него на полке стоит 5 полных горшочков и 6 пустых. Какова вероятность, что из взятых случайно трех горшочков один окажется полным?

2) Три стрелка стреляют по мишени. Вероятность попадания первого – 0,6, второго – 0,7, третьего 0,8. Найти вероятность того, что при одном залпе обнаружится не более одного попадания ?

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,3	0,4	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ n⁵

ⁿ⁼¹ 3ⁿ⁺¹

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, 0< x £ 12}; B = {2x: x ÎN, -1< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 4.

1. Решить задачи:

1) Ребенок раскладывает в ряд кубики с буквами о, в, л, а, г. Какова вероятность, что он получит слово «волга»?

2) В семье трое детей. Найти вероятность того, что среди этих детей ровно два мальчика. (Вероятность рождения мальчика 0,52)

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,3	0,3	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ n² + 1

ⁿ⁼¹ 3ⁿ

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, -10< x £ 3}; B = {4x: x ÎN, -3< x £ 1}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 5.

1. Решить задачи:

1) На фирме работает 6 женщин и 8 мужчин. Случайным образом выбирают три фамилии. Какова вероятность того, что из них две принадлежат мужчинам и она – женщине?

2) В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны 0,1 0,15 0,2. Найти вероятность того, что тока в цепи не будет.

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,2	0,4	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ n²

ⁿ⁼¹ 2ⁿ

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, - 6 < x £ 11}; B = {x/2: x ÎN, -10 < x £ 10}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 6.

1. Решить задачи:

1) В группе устраивают новогоднюю лотерею, продавая 40 билетов по 10 рублей. Выигрывают 3 билета по 101 рублю, а остальные по 1 рублю. Найдите вероятность того, что за два купленных билета участник выиграет ровно 102 рубля.

2) Для разрушения моста достаточно попадания одной авиационной бомбы. Вероятности попадания первой, второй и третьей бомбы соответсвенно равны 0,4; 0,6 и 0,7. Найти вероятность того, что мост будет разрушен.

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,5	0,1	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ n + 5

ⁿ⁼¹2ⁿ

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, - 4 < x £ 13}; B = {2x: x ÎN, -1< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 7.

1. Решить задачи:

1) Студент знает ответ на 22 вопроса из 30. какова вероятность, что он знает ответ на два из предложенных ему трех вопросов?

2) Три стрелка стреляют по мишени. Вероятность попадания первого – 0,5, второго – 0,7, третьего 0,9. Найти вероятность того, что при одном залпе обнаружится не более одного попадания ?

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,2	0,4	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ 2n – 1

ⁿ⁼¹ 2ⁿ

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, 1 < x £ 19}; B = {2x+1: x ÎN, -1< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 8.

1. Решить задачи:

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,5	0,1	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ 2ⁿ

ⁿ⁼¹n¹⁰

3. Задать множества А и В, указав все их злементы, если А = {x: x ÎN, -5 < x £ 9}; B = {2x-1: x ÎN, -1< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 9.

1. Решить задачи:

1) Вини Пух берет с полки горшочки с медом и пустые возвращает обратно, чтобы не портить внешний вид. У него на полке стоит 6 полных горшочков и 7 пустых. Какова вероятность, что из взятых случайно трех горшочков один окажется полным?

3) Дискретная случайная величина задана законом распределения:

Х
Р	0,3	0,3	Р₃

2. Исследовать ряд на сходимость:

_∞

∑ n²

ⁿ⁼¹ 3ⁿ

3. Задать множества А и В, указав все их злементы, если А = {2x: x ÎN, -3< x £ 4}; B = {x+3: x ÎN, -10< x £ 5}

Найти сумму (объединение) и произведение (пересечение) этих множеств

Вариант 10.

1. Решить задачи:

1) Ребенок раскладывает в ряд кубики с буквами о, в, л, а, г. Какова вероятность, что он получит слово «волга»?

2) Для разрушения моста достаточно попадания одной авиационной бомбы. Вероятности попадания первой, второй и третьей бомбы соответсвенно равны 0,5; 0,6 и 0,8. Найти вероятность того, что мост будет разрушен.

3) Дискретная случайная величина задана законом распределения: