Расчет многоканальных систем с отказами и бесконечным потоком требований на входе (разомкнутые системы)

Для нахождения предельных вероятностей состояний составляется система уравнений Колмогорова. Ниже приведены конечные формулы для расчета вероятностей состояний, выведенные из системы уравнений Колмогорова.

, ,

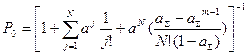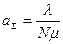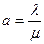
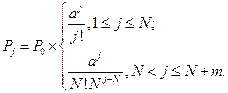
вероятность загрузки системы:

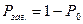
вероятность отказа в обслуживании:

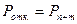, в случае если заняты все каналы и все места в очереди заявка получает отказ.

среднее число требований в очереди:

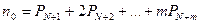
среднее время ожидания в очереди:

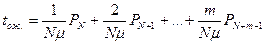
среднее число занятых каналов:

)

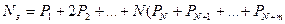среднее число заявок в системе:

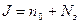, т.е. среднее число заявок в очереди плюс среднее число занятых каналов;

среднее время пребывания требования в системе:

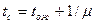, т.е. среднее время ожидания в очереди плюс среднее время обслуживания.

Расчет многоканальных систем без потерь с источником конечного числа требований (замкнутые системы)

Для нахождения предельных вероятностей состояний составляется система уравнений Колмогорова. Ниже приведены конечные формулы для расчета вероятностей состояний, выведенные из системы уравнений Колмогорова.

,

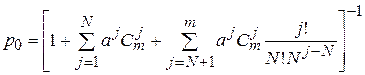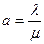
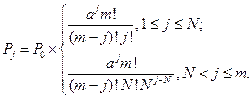
вероятность загрузки системы:

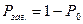
вероятность отказа в обслуживании:

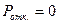, т.к. любая заявка будет рано или поздно обслужена

среднее число требований в очереди:

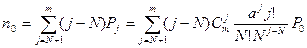
среднее время ожидания в очереди:

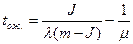
среднее число заявок в системе:

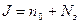, т.е. среднее число заявок в очереди плюс среднее число занятых каналов;

среднее число занятых каналов:

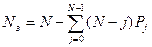
среднее время пребывания требования в системе:

.

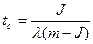4. СМО с «взаимопомощью» между каналами

СМО с «взаимопомощью» - системы, в которых одна и та же заявка может обслуживаться несколькими каналами. Взаимопомощь может быть организована в любом типе СМО (замкнутая, разомкнутая).

При анализе таких СМО необходим учет 2-х факторов:

1. Насколько убыстряется дисциплина обслуживания заявки при работе нескольких каналов. Самый простой вариант – пропорциональное увеличение: 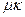, где k – число каналов, занятых обслуживанием заявки.

2. Дисциплина взаимопомощи. Самый простой вариант – «все как один». Заявку обслуживают сразу все каналы.

Выгодно или нет вводить «взаимопомощь» зависит от реальной СМО и ее параметров.

Пример. Трехканальная СМО с потерями и бесконечным потоком заявок на входе.

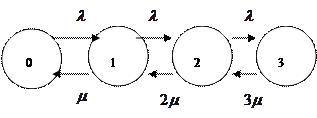Размеченный граф состояний для СМО без «взаимопомощи»

Размеченный граф состояний для системы с «взаимопомощью»

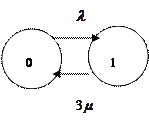Далее, для нахождения предельных вероятностей состояний, необходимо составить систему уравнений Колмогорова.