Властивості незвідних многочленів

Властивості подільності многочленів

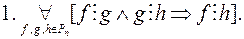
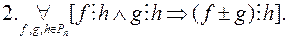
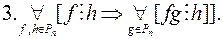
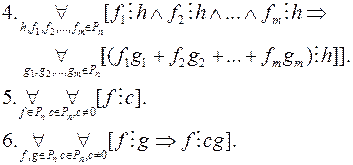
Означення 4. Многочлен 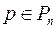називається незвідним у полі 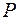, якщо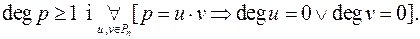

Многочлен 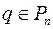називається звідним у полі 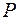, якщо

Властивості незвідних многочленів

1. Якщо незвідний у , то і будь-який асоційований з ним многочлен 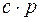незвідний у .

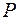2. Якщо 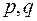незвідні у 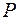многочлени і 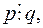то 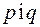- асоційовані.

3. Будь-який многочлен 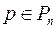першого степеня незвідний у .

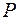Можливість і єдиність розкладу многочлена у добуток незвідних множників - залишається в силі і в кільці 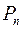при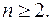

Теорема 13. Будь-який многочлен 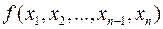над полем 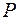не нульового степеня можна подати як добуток многочленів, незвідних у полі .

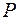Раціональні дроби від кількох змінних

Кільце 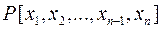многочленів від 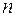змінних, так само як і кільце 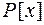многочленів від однієї змінної, можна «вкласти» у поле відношень 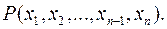Точніше, можна побудувати таке поле 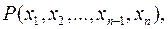яке містить 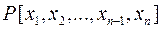як підкільце і кожний елемент якого можна подати як частку 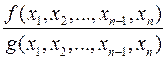двох многочленів

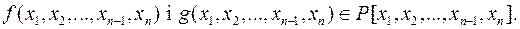
Таке поле єдине з точністю до ізоморфізму.

Елементи теорії виключення. Результант двох многочленів

Многочлен 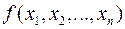від кількох змінних можна також розглядати як алгебраїчне рівняння ( ).

( )

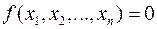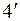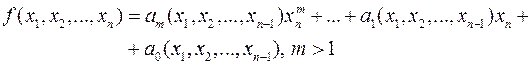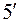вибрати в 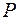довільні значення 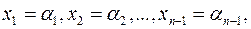при яких 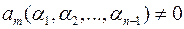такі значення обов’язково знайдуться, бо 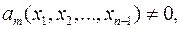підставити їх у коефіцієнти многочлена ( 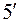) і дістати многочлен

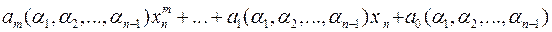
від однієї змінної степеня 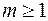над полем 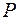. За теоремою Кронекера, цей многочлен має корінь 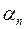у полі 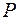, або у деякому його розширенні. Але тоді 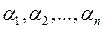- розв’язок рівняння ( ).

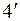Більш поширеною і практично застосовною є задача розв’язування систем алгебраїчних рівнянь виду

( )

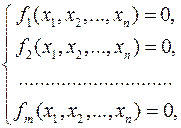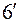тобто знаходження спільних розв’язків усіх многочленів

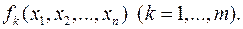
Нехай задано систему двох алгебраїчних рівнянь з двома невідомими. Розмістимо члени цих рівнянь за степенями одного з невідомих (їх ліві частини розглядаються над полем ):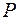

( )

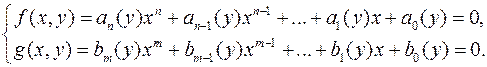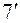і припустимо, що пара елементів 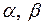є розв’язком системи (30), тобто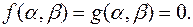

Зрозуміло, що з системи (30) можна утворити цілий ряд вивідних рівнянь, для яких 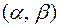також буде розв’язком.

Підставимо в рівняння системи ( 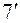), що має розв’язок 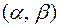, значення 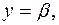дістанемо два рівняння з одним невідомим:

( )

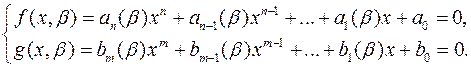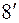причому 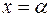є спільним коренем обох цих рівнянь. Оскільки два довільно взяті рівняння з одним невідомим, взагалі кажучи, спільних коренів не мають, то рівняння системи ( 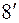), які мають спільний корінь, не можуть бути незалежними. Між їх коефіцієнтами повинен бути деякий зв’язок. Якщо ми знайдемо цей зв’язок між коефіцієнтами 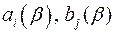, тобто співвідношення

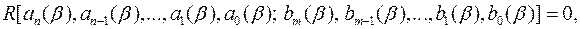то тим самим дістанемо деяке рівняння

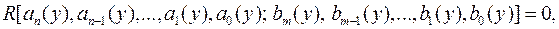
яке повинно задовольнятись при 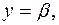щоб 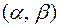могло бути розв’язком системи.

Отже, треба розв’язати таку задачу. Нехай дано систему двох рівнянь з одним невідомим:

( )

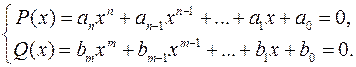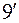Знайти, при яких умовах ці рівняння можуть мати спільний корінь.

Зауважимо, що між системами ( 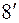) і ( 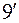) є певна відмінність. При розгляді системи ( 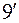) природно вважати, що 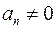і 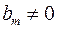, тоді як у системі ( 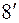), утвореній з ( 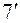) при 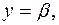деякі з коефіцієнтів і, зокрема старші коефіцієнти 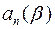і 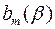, можуть дорівнювати нулю, хоч відповідні многочлени 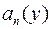і 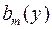не були нулями.

Очевидно, що спільні корені рівнянь системи треба шукати лише серед коренів многочлена 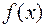. Позначимо ці корені через 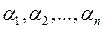. З другого боку, 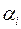лише тоді буде спільним коренем, якщо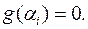

Означення 5. Результантом многочленів

( )

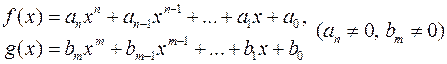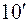називається вираз

, (*)

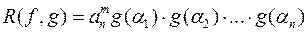де 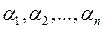- корені многочлена .

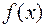Зауваження. 1. У цьому означенні многочлени 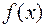і 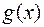нерівноправні; для 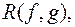дістаємо:

, (**)

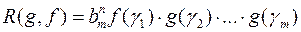де (**) 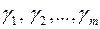- корені многочлена .

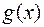На перший погляд здається, що це є недоліком введеного означення (бо в поставленій задач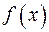і і 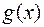рівноправні), проте можна показати, що 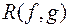і 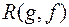можуть відрізнятися лише знаком.

2. Щоб означити для двох многочленів один з результантів 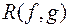або 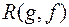, потрібно, щоб хоч один з старших членів цих многочленів був відмінний від нуля.

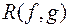є симетричним многочленом від 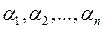, коефіцієнти якого раціонально виражаються через 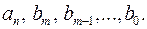Із основної теореми теорії симетричних многочленів випливає, що 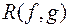можна подати як многочлен від основних симетричних функцій

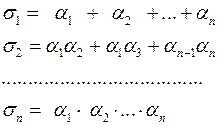
Оскільки 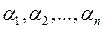- корені многочлена 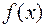, то 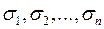, за формулами Вієта, раціонально виражаються через його коефіцієнти 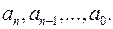Отже, остаточно 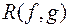можна раціонально виразити через коефіцієнти 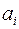і 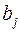обох заданих многочленів. Звідси випливає, що результант довільних двох многочленів над полем 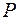є елементи цього самого поля.

Властивості результанта

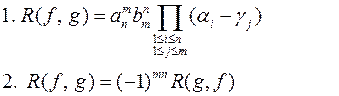
Теорема 14. Для того, щоб многочлени 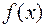і 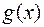мали спільний корінь, необхідно і достатньо, щоб їх результант дорівнював нулю.

Означення 6.Дискримінантом 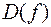многочлена 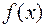називається вираз

, (***)

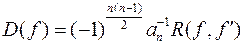де 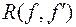- результант многочлена 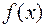і його похідної .

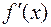Теорема 15. Многочлен 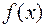має кратний корінь тоді і тільки тоді, коли його дискримінант дорівнює нулю.

Результант у формі Сільвестра

Нехай дано два многочлена

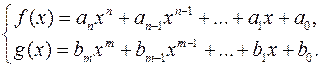
Побудуємо детермінант із 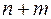рядків із коефіцієнтів 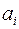і .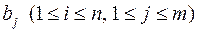

( )

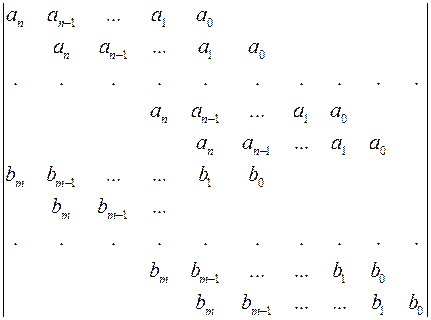
Форма Сільвестра важлива тим, що вона дає можливість узагальнити поняття результанта, введене в означенні 5. Ми бачили, що при 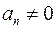детермінант Сільвестра збігається з 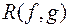, означеним формулою (*). Аналогічно при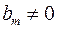 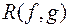дорівнює відповідному детермінанту Сільвестра. Але якщо 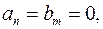то формули (*) – (**) результанта 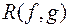або 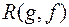втрачає смисл, тоді як детермінант Сільвестра зберігає смисл, хоч і набуває значення нуль.

У зв’язку з цим надалі під результантом 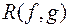двох многочленів ми розумітимемо детермінант Сільвестра для цих многочленів.

При новому означенні результанта властивість 1 втрачає смисл (при 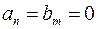), але залишається в силі властивість 2

,

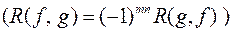що можна перевірити, переставляючи рядки детермінанта ( ).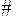

Теорема 14. Якщо результант 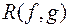дорівнює нулю, то або а) многочлени 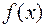і 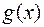мають спільний корінь, або б) обидва їх старші коефіцієнти дорівнюють нулю.

Теорема 15. Якщо многочлени 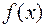і 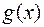мають спільний корінь, то 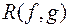дорівнює нулю.

Розв’язання системи алгебраїчних рівнянь

Нехай дано систему двох алгебраїчних рівнянь з двома невідомими з коефіцієнтами із 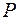. Розмістивши члени цих рівнянь за степенями одного невідомого, матимемо

( )

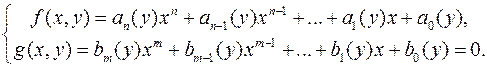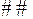Розглядаючи 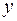як параметр, побудуємо для многочленів 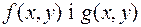результант :

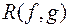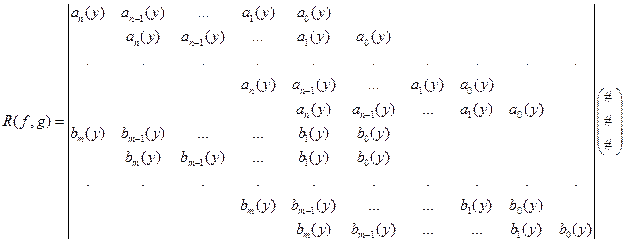
Позначимо цей результант через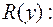

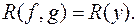
Як видно з , 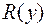дістаємо з коефіцієнтів 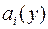і 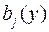за допомогою дій додавання і множення. Тому, результант многочленів 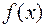і 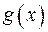є многочленом від 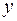над тим самим полем 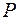. Позначимо степінь многочленна 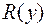через 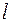. Тоді, результант многочленів 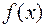і 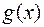є многочленом від 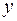над тим самим полем 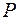. Позначимо степінь многочлена 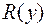через 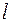. Тоді, степінь 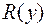не перевищує добутку степенів многочленів 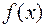і 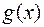(відносно обох змінних). Многочлен 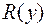має в полі розкладу 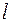коренів 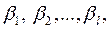тобто 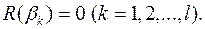Але те, що результант дорівнює нулю, на основі теореми 14 означає, що многочлени

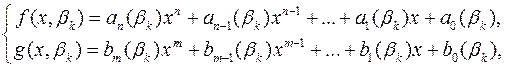
або мають спільний корінь, або їх старші коефіцієнти 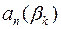і 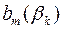дорівнюють нулю.

Розглянемо обидва випадки.

а) Хоча б один з коефіцієнтів 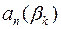і 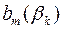не дорівнює нулю.

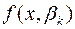У цьому випадку многочлени і 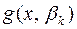мають спільний корінь. Позначимо його через 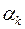. Пара 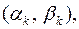очевидно, є одним з розв’язків системи (38), або 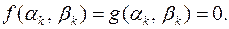Зауважимо, що для даного значення 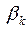ми можемо мати не один, а кілька спільних коренів многочленів 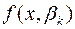і 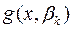, наприклад 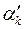і 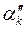. Тоді, очевидно, обидві пари 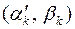і 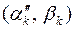є розв’язками системи (38).

б) Обидва коефіцієнти 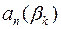і 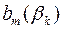дорівнюють нулю.

У цьому випадку, незважаючи на те, що результант дорівнює нулю, 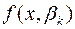і 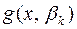можуть не мати спільного кореня. Якщо це так, то корінь результанта 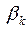слід відкинути. Проте може статися, що й у цьому випадку многочлени 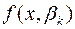і 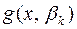мають спільний корінь 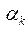. Тоді знову 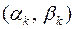є розв’язком системи (38).

Щоб знайти всі розв’язки системи (38), треба аналогічно розглянути всі корені результанта .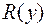

Зауважимо, що крім знайдених таким способом розв’язків ніяких інших розв’язків система мати не може.

Як висновок всього сказаного можна запропонувати таку схему дій при розв’язуванні системи рівнянь з двома невідомими.

1. Побудувати результант ( 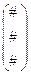) і знайти всі його корені.

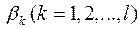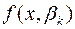2. Знайдений корінь підставити в многочлени системи ( ). Дістанемо многочлени і .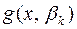

3. Знайти спільний найбільший дільник 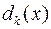многочленів 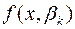і .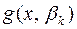

4. Розв’язати рівняння 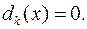Корені цього рівняння 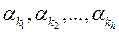є, очевидно, спільними коренями многочленів 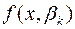і .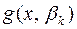

5. Скласти систему пар 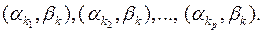Ці пари є розв’язками системи ( 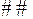), які відповідають кореню .

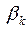Дії 2 – 5 слід виконати окремо для кожного з коренів 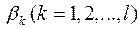. При цьому слід мати на увазі, що для деяких коренів результанта може не існувати спільних коренів многочленів 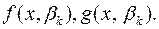Це може бути тоді, коли 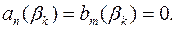Ознакою відсутності спільних коренів, очевидно, є те, що многочлени 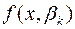, 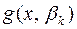взаємно прості, тобто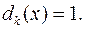

У тих випадках, коли корені 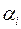одного з многочленів 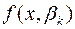, 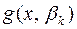легко знайти, шукати найбільший спільний дільник 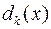недоцільно: досить перевірити, які з коренів 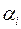є коренями і другого многочлена.

Ми розглянули як розв’язується система двох алгебраїчних рівнянь з двома невідомими. Цю теорію можна застосувати і до розв’язування системи 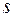алгебраїчних рівнянь з 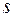невідомими.

Зауважимо, що взагалі виключення невідомих методами елементарної алгебри в більшості випадків і є знаходженням результанта. Потім за коренем 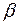результанта знаходять спільний корінь многочленів 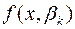, 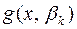. Спільність кореня перевіряють підстановкою, що обов’язково слід робити при розв’язуванні таких систем у школі.

Симетричні многочлени

Означення.Многочлен 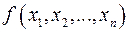називається симетричним відносно змінних 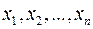, якщо внаслідок довільної перестановки змінних 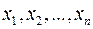утворюється многочлен, який дорівнює даному.