Построение линейных многошаговых методов решения задачи Коши
Рассмотрим задачу Коши 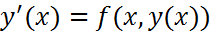 ,
, 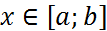 (1) и
(1) и 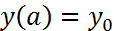 (2). На
(2). На 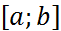 введем равномерную сетку
введем равномерную сетку 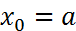 ,
, 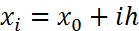 ,
, 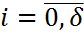 . Линейные многошаговые методы задаются соотношением
. Линейные многошаговые методы задаются соотношением
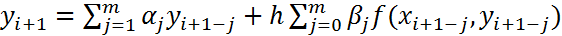 ,
, 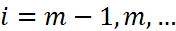 (3). Для начала вычислений по формуле (3) необходимо знать разгонные значения.
(3). Для начала вычислений по формуле (3) необходимо знать разгонные значения. 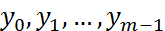 . Значение
. Значение 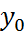 берется из (2), остальные
берется из (2), остальные 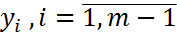 определяются посредством одношагового метода соответствующего порядка точности.
определяются посредством одношагового метода соответствующего порядка точности.
Числа 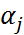 и
и 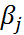 в (3) будем называться параметрами метода (3). При
в (3) будем называться параметрами метода (3). При 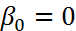 (3) будем явным методом, а при
(3) будем явным методом, а при 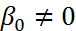 – неявным методом.
– неявным методом.
Пусть 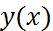 точное решение задачи (1), (2). Погрешность метода (3), как правило, удовлетворяет оценке
точное решение задачи (1), (2). Погрешность метода (3), как правило, удовлетворяет оценке
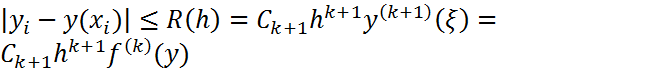 где
где 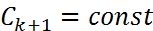 . В основу построения многошаговых методов (3) (т.е. выбора
. В основу построения многошаговых методов (3) (т.е. выбора 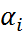 и
и 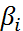 ) положим понятие алгебраического порядка точности. Будем говорить, что метод (3) имеет алгебраический порядок точности, равный
) положим понятие алгебраического порядка точности. Будем говорить, что метод (3) имеет алгебраический порядок точности, равный 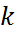 , если он является точным для любого многочлена степени
, если он является точным для любого многочлена степени 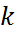 . Если
. Если 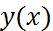 – многочлен степени
– многочлен степени 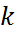 , то
, то 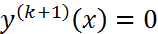 , т.е.
, т.е. 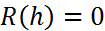 .
.
Для построения метода (3) алгебраического порядка точности равного 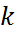 , будем поочередно подставлять в (3) функции вида:
, будем поочередно подставлять в (3) функции вида: 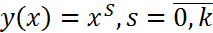 . При
. При 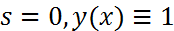 . В силу (1)
. В силу (1) 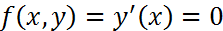 . Далее
. Далее 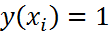 , необходимо чтобы выполнялось
, необходимо чтобы выполнялось 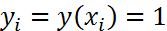 точно, поэтому при подстановке функции
точно, поэтому при подстановке функции 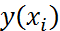 будем иметь соотношение
будем иметь соотношение 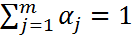 (4)
(4)
Таким образом, условие (1) является необходимым и достаточным для того, чтобы метод (3) был точен для любого многочлена нулевой степени. Положим теперь 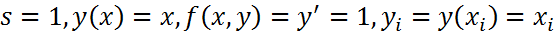 . Подставляя эти соотношения в (3) будем иметь:
. Подставляя эти соотношения в (3) будем иметь: 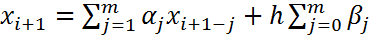 . Последнее соотношение перепишем так:
. Последнее соотношение перепишем так:
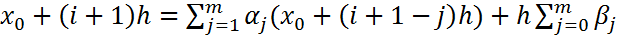 .
.
В силу (4), последнее равенство запишем в виде:
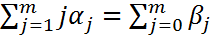 (5)
(5)
Таким образом, для того, чтобы метод (3) имел алгебраический порядок точности, равный 1, необходимо и достаточно, чтобы его параметры удовлетворяли условиям (4) и (5). Продолжая этот процесс, получим соотношение 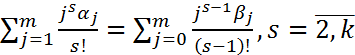 (6)
(6)
Т.е. для того, чтобы метод (3) имел алгебраический порядок точности равный необходимо и достаточно, чтобы его параметры удовлетворяли (4), (5), а при  еще и (6). Соотношение (4) и (5) (или (4),(5),(6)) представлял собой систему линейных алгебраических уравнений, которая в общем случае может иметь не единственное решение. Поэтому, ряд параметров метода (3), имеющий алгебраический порядок точности равный
еще и (6). Соотношение (4) и (5) (или (4),(5),(6)) представлял собой систему линейных алгебраических уравнений, которая в общем случае может иметь не единственное решение. Поэтому, ряд параметров метода (3), имеющий алгебраический порядок точности равный 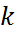 , будут свободными. Т.е. ими можно распорядиться, например, для повышения алгебраического порядка точности или повышения устойчивости, либо чтобы сделать метод (3) явным.
, будут свободными. Т.е. ими можно распорядиться, например, для повышения алгебраического порядка точности или повышения устойчивости, либо чтобы сделать метод (3) явным.
Пример. Пусть (3) имеет вид: 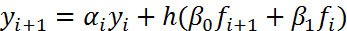 (7). Обозначим
(7). Обозначим 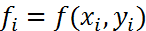 . В данном случае условия (4) и (5) таковы
. В данном случае условия (4) и (5) таковы 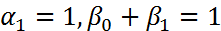 . Поэтому (7) можно переписать в виде
. Поэтому (7) можно переписать в виде 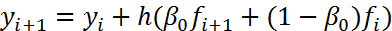 (8).
(8).
Метод (8) точен для любого многочлена первой степени и содержит 1 свободных параметр 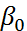 . Например, если положить
. Например, если положить 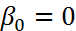 , то получим явный метод, который является методом Эйлера. Однако, например
, то получим явный метод, который является методом Эйлера. Однако, например 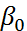 можно выбрать и таким образом, чтобы метод (8) был точен для любого многочлена второй степени. Действительно, будем подставлять в (8) функцию:
можно выбрать и таким образом, чтобы метод (8) был точен для любого многочлена второй степени. Действительно, будем подставлять в (8) функцию: 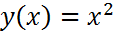 . В данном случае:
. В данном случае:
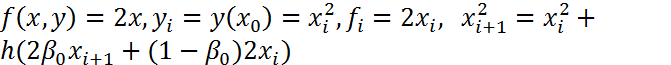 (9). Перепишем (9) в виде:
(9). Перепишем (9) в виде: 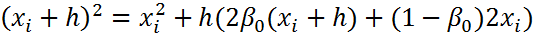 (10)
(10)
Приведем в (10) подобные слагаемые:
 .
.
А (8) приобретает вид: 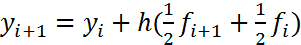 .
.
