Структуралардың изоморфизмі

А₁ , А₂, ... , А_t аксиомаларының системасы қайшылықсыз, және сондықтан негізгі қатынастары ∆₁, ∆₂, ... , ∆_к болатын Т текті структураларды анықтайтын болсын.

М^/ жиыны үстінде Δ_i қатынастарға нақты ∆^/₁, ∆₂^/, ... , ∆_к^/ мағыналар берілсінде, солар бойынша А₁ , А₂, ... , А_t аксиомаларының бәрі де орындалатын болсын. Сонда М^/ жиыны үстінде 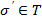структурасы анықталады деуге болады. Сондай әдіспен М^// жиыны үстінде Δ_i қатынастарының нақты ∆^//₁, ∆₂^//, ... , ∆_к^// мағыналары болатындай 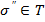структурасы анықталсын. Егер

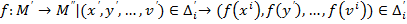
Яғни 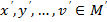элементтері 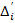қатынасында, оларға сәйкес

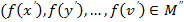
элементтері 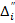қатынасында биекция бар болса, онда 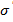және структуралары изоморфты структуралары деп аталды. Мысалы. Т абелдік группа структурасының тегі болсын. Осы тектегі нақты екі структураны қарстырайық:

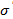- аддитивтік группа ретінде нақты сандардың R жиыны,

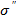- мультипликативтік группаретінде оң сандардың R₊ жиыныы.

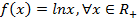
заңы арқылы берілетін 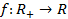, биекциясын қарастырайық.

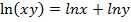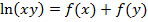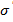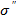болатындықтан , демек, және структуралары изоморфты структуралар болады.

Үстінде σ структурасы анықталған М жиынының өзіне – өзінің изоморфизмі сол жиынның автоморфизмі деп аталады.

Мылалы. n өлшемді векторлық кеңістіктің үстінде анықталған әрбір азғындамайтын сызықтық оператор сол кеңістіктің автоморфизмі болып табылады.

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:

Дәріс тақырыбы: Аксиомалар жүйесiнің қайшылықсыздығы тәуелсiздiгi және толыктығы

Жоспары:

1. Аксиомалар жүйесінің қарама-қайшылықсыздығы.

2. Аксиомалар жүйесінің тәуелсіздігі.

3. Аксиомалар жүйесінің толықтығы.

Дәріс тезисі

Біз бір А₁ , А₂, ... , А_t аксиомаларының системасын тұжырымдадық дедік. Ол аксиомалар системасы арқылы анықталатын Т текті структуралар туралы сөз етуден бұрын 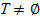екенін тексеру керек.

Ол үшін осы аксиомалар системасының бір интерпретациясын құру жеткілікті болатындығын білеміз. Интерпретацияны құрғанда біз системаның ішк қайшылықтары болмайтындығына көзімізді әбден жеткізетін «жеткілікті түрде сенімді» ұғымдарды ғана пайдалануымыз керек. Тек сол жағдайда ғана А₁ , А₂, ... , А_t аксиомаларының ситемасы ішкі қайшылықсыз болады және 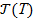теориясынан, біз ол теореманы қаншалықты ұзаққа дамытсақта бірін-бірі теріске шығаратын екі теорема шықпайды.

Егер А₁ , А₂, ... , А_t аксиомаларының системасы қайшылықсыз болса, онда ол система ешқандай структураны анықтамайды: қатынастарда А₁ , А₂, ... , А_t қасиеттері боларлық база - E, F, G жиындары болмайды. Сондықтан аксиомалардың ондай системасы пайдасыз болады, айтуға тұрарлық нәтиже бермейді.

Сонымен, біз 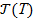теорясын құратын А₁ , А₂, ... , А_t аксиомаларының системасы қайшылықсыз болу керек. Бұл асиомалар системасының қандай да болса да қойылатын аса манызды талап.

Жоғарыда айтылғандай, аксиомалар системасының ішкі қайшылықсыздығы жөніндегі мәселені тек математикалық логика заңдары арқылы ғана шешуге болады.

Геометрияда қарастырылатын аксиомалар системаларының структураларын анықтайтын интерпретациялар құрғанда біз әр түрлі сандар жиынын пайдаланамыз. Сондықтан берілген А₁ , А₂, ... , А_t аксиомаларының системасы қайшылықсыздығын, математикалық логика заңдарына сүйенбей-ақ, біз мына ұйғарымға келеміз. «Егер арифметика қайшылықсыз болс, онда А₁ , А₂, ... , А_t аксиомаларының системасы да қайшылықсыз».

Бізге 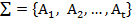аксирмаларының системасы айқын тұжырымдалған базаның E, F, G жиындары үстінде анықталатын ∆₁, ∆₂, ... , ∆_к қатынастары қанағаттандыратын, талаптардың тізбесі екендігі мәлім, бірақ мұндағы қатынастардың өздері E ×F× G декарттық көбейтіндінің бөлімше жиындары ретінде анықталып берілмеген. ∑ аксиомаларының системасы 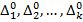нақты қатынастардың 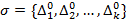системаларының ∑ системасындағы аксиомалардың бәрін де қанағаттандыратын бүкіл Т жиынын анықтайды.

Аксиомалардың ∑ системасы қайшылықсыз болсын, басқаша айтқанда, Т текті структуралардың 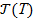теориясын құру мүмкін болсын. Сонда мынадай сұрақ туады: берілген текті структураларды анықтау үшін ∑ системасындағы аксиомалардың бәрі де қажет пе, яғни, Т жиынын өзгертпей, айтылып отырған аксиомалардың санн кемітуге болмас па екен?

А аксиомасы ∑ системасындағы аксиомалардың бірі және 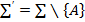болсын. Егер 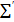системасының кез келген интерпретациясы ∑ системасының да интерпретация болып табылса, онда А аксиомасы ∑ системасының қалған аксиомаларына тәуелді аксиома деп аталады.

Бұл жағдайда 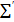системасының аксиомалары орындалса, А аксиомасы да орындалады. Демек, 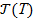теориясында А сөйлемі ∑ системасындағы қалған аксиомалардың салдары болады.

∑ системасындағы бір А аксиомасын оны теріке шығаратын 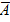аксиомасымен ауыстырайық та, аксиомалардың содан кейін құрылған жаңа системасын 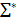деп белгілейік. Сонда: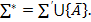 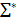системасының әрбір интерпретциясы 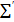системасының интерпретациясы болады. Егер А аксиомасы ∑ системасының қалған аксиомаларына тәуелді болса, онда А аксиомасы 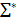системасының интерпретациясында да орындалуға тиіс. Бірақ Δ_i қатынастарының қайсысыболса да әрі А, әрі 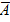аксиомаларының қасиеттеріне қатарынан ие бола алмайды.

Сондықтан, А аксиомасы ∑ системасының қалған аксиомаларыа тәуелді болса, онда аксиомалардың 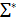системасы қайшылықты болып шығады.

Сонымен, 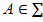аксиомасының ∑ системасындағы қалған аксиомаларға тәуелсіздігін дәлелдеу үшін, аксиомалардың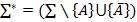

Системасы мағынасы бойынша қайшылықсыз болатындығын дәлелдеу жеткілікті.

Мысалы. Абельдік группалар структурасын анықтайтын аксиомалардың системасы 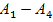аксиомаларынан және

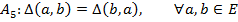
аксиомасынан құралады. А₅ аксиомасының 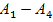акиомаларына тәуелсіз екенін дәлелдейік.

Ол үшін аксиомалардың 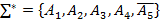системасының қайшылықсыздығын дәлелдеу жеткілікті, мұндағы 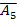аксиомасы А₅ аксиомасының терістеуі, атап айтқанда

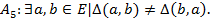
Алайда 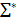системасының қайшылықсыздығы коммутативті емес группалардың болуынан шығады.

Егер А аксиомасы ∑ системасындағы аксиомалардың қалғандарына тәуелді болса. Онда оны аксиомалар тізімінен шығарып сызып тастап, 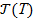теориясын тек 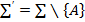системасының ғана аксиомаларын пайдаланып құруға болады.

Әрине, ∑ системасындағы аксиомалардың әрқайсысы қалғандарына тәуелсіз болғаны жақсы. Кейде берілген ∑ системасындағы аксиомалардың қалғандарына тәуелділерін біртіндеп тауып алып, сызып тастап, аксиомалары біріне-бірі тәуелсіз система құрастыруға болады.

Алайда берілген ∑ системасындағы кейбір аксиомалардың сол системалардың қалған аксиомаларына тәуелділігі немесе тәуелсіздігі жөнінде мәселе қою мағынасыз болады. Мысалы, группаның структурасын анықтайтын 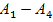аксиомаларының системасында А₃ аксиомасының сол системадағы қалған үш аксиомаға тәуелділігі немепсе тәуелсіздігі жөнінде мәселе қою орынсыз болады, өйткені А₄ аксиомасын тұжырымдағанда А₃ аксиомасы орындалады деп есептеледі.

Ескертпе. Егер А аксиомасы ∑ системасындағы қалған аксиомаларға тәуеліз болса, онда аксиомалардың 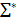системасы қайшылықсыз болады және ол Т текті структураларды анықтайды. Ондай жағдайлармен III тарауда, Гильберт аксиомаларының системасын қарастырғанда, кездесеміз.

∆₁, ∆₂, ... , ∆_к қатынастарының қасиеттерін сипаттайтын аксиомалардың қайшылықсыз ∑ системасы берілсін. Төмендегі шарттарды қанағаттандыратын А аксиомасы бар делік:

а) А аксиомасы жаңа қатынастар туғызбайды;

б) ол ∑ системасының аксиомаларына тәуелсіз;

в) аксиомалардың 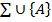системасына қайшылықсыз.

Осы үш шарт орындалғанда аксиомалардың ∑ системасы толымсыз система деп аталады. Ал егер ондай А аксиомасы болмаса, онда ∑ системасы аксиомалардың толық системасыдеп аталады.

Аксиомалардың ∑ системасы толымсыз болмын, яғни жоғарыда айтылған а), б), в) шарттарды қанағаттандыратын А аксиомасы табылсын. Сонда в) шарты бойынша аксиомалардың 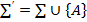системасы қайшылықсыз болады, ал б) шарты бойынша А аксиомалардың ∑ системасындағы аксиомаларға тәуелсіз болғандықтан, аксиомалардың 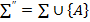системасы қайшылықсыз болады. 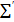системасының интерпретацияларының бірін 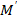арқылы, 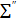системасының интерпретацияларының бірін 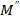арқылы белгілейік. 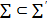және 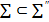болғандықтан, 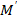және 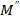интерпретациялары да аксиомалардың ∑ системасының интерпретациялары болып табылады.

Бірақ 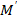интерпретациясында А аксиомасы орындалып, 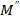интерпретациясында А аксиомасы орындалатындықтан, ∑ системасыүші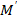н пен 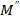интерпретациялары изоморфты болмайды.

Сонымен, аксиомалардың ∑ системасы толымсыз болса, онда оның өзара изоморфты болмайтын интерпретациялары болады. Сондықтан, аксиомалардың ∑ системасының толық екендігін дәлелдеу үшін, оның барлық интерпретацияларының өзара изоморфты екендігін дәлелдеу жеткілікті болады.

1-мысал. Біз кітаптың 2-бөлімінде R өрісі үстіндегі барлық n өлшемді аффиндік А_n кеңістіктері изоморфты болатындығын дәлелдегенбіз. Сондықтан, R өрісі үстіндегі n өлшемді аффиндік кеңістікке арналған Вейль аксиомаларының {1,2} системасы толық система болады.

R өрісі үстіндегі n өлшемді евклидтік Е_n кеңістікке арналған Вейль аксиомаларының {1,2,3} системасы толымдылық қасиеті болады.

Мәселе мынада:айтылып отырған 3-аксиома системаға жаңа қатынас көшірулер кеңістігінде векторлардың ортогональдық қатынасын енгізеді. Сондықтан Е_n кеңістігінің {1,2,3} аксиомалары анықтайтын Т структурасының тегінен өзгеше болады және 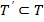болады.

2-мысал. Группалар структурасын анықтайтын 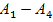аксиомаларының системасына жаңа қатынас енгізбейтін және алдыңғыларға тәуелсіз А₅ аксиомасын қосу арқылы қайшылықсыз 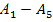аксиомаларының системасын құруға болатындығы 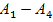аксиомалар системасының толымсыздығы жөнінде қорытынды жасауға мүмкіндік береді.

Аксиомалардың ∑ системасы қайшылықсыз және Т текті структураларды анықтайтын болсын. Егер осы структуралардың бәрі изоморфты болса, онда 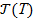теориясын бір мәнді теория дейді. Ал, Т текті структуралардың кейбіреуі ғана изоморфты болып, кейбіреулері изоморфты болмаса, онда 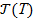теориясын көп мәнді теория дейді.

Біз енді А_n кеңістігінің геометриясы мен Е_n кеңістігінің геометриясы - бір мәнді теориялар, ал группалар теориясы - көп мәнді теория дей аламыз. «Көп мәнді теорияларды зерттеу - қазіргі математиканың классикалық математикадан айырмашылығын сипаттайтын ең көрнекті белгісі».

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:

Модуль №2.Евклид геометриясы (лек 6с, прак 7с., СӨЖ 24с)