Потенциалы электромагнитного поля в вакууме

Удобно ввести:

-векторный потенциал

-скалярный потенциал

однозначно определяют электромагнитное поле

Градиентная инвариантность.

Существует преобразование, которое не меняет полевых характеристик . Таким преобразованием является градиентное:

Здесь 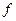– произвольная функция координат и времени

-инвариантность полевых характеристик

относительно градиентных преобразований.

Аналогично для :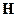

На потенциалы могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к. - произвольная.

Функция.

Пусть имеется функция Хевисайда:

Ясно, что кроме , производная везде равна нулю. Рассчитаем интеграл:

, ,

Рассмотрим этот же случай, но картинка смещена на :

Интегральное одномерное соотношение:

Существует множество способов моделирования подобных функций.

Если , то (3) это :

Рассмотрим простейший случай.

- площадь под графиком функции:

Делим пополам.

И так далее до бесконечности. Это одна из простейших моделей 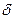-функции.

Объёмная плотность точечного заряда.

Рассмотрим систему из точеченого заряда

Здесь возникает необходимость использовать 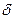-функцию.

Тогда:

Это соответствует случаю, когда заряд помещён в начало координат, а плотность заряда ищется в точке, с радиус-вектором .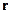

Если же заряд помещён не в начало отсчёта, то плотность заряда перепишется в следующем виде:

В случае системы точечных зарядов имеем:

Для изображения плотности точечного источника всегда используется 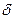-функция.

Закон сохранения заряда.

Запишем уравнение Максвелла: . Подействуем на него оператором 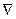скалярно. Получаем:

Но дивергенция всякого ротора равна нулю, поэтому в результате получаем:

- уравнение непрерывности

Проинтегрируем обе части этого уравнения по некоторому объёму:

, где 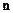-единичный вектор нормали

определяет количество заряда выносимого через поверхность объёма. Если - острый, то заряд выносится из объёма и -положителен. Если тупой, то заряд приходит в объём и - имеет знак минус.

Типы калибровок.

Перепишем уравнения Максвелла:

1.Калибровка Лоренца

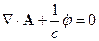
Тогда уравнение первое уравнение Максвелла перепишется в следующем виде:

- уравнение Даламбера

Это уравнение есть – неоднородное дифференциальное уравнение в частных производных.

- оператор гиперболического типа.

Для 4-го уравнения Максвелла имеем:

Все, имеющие физический смысл, результаты должны быть градиентно-инвариантыми:

В силу калибровки Лоренца получаем:

Т.е. функция 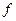должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)

2.Калибровка Кулона

- калибровка Кулона

Уравнение (А) перепишется в следующем виде:

- уравнение Пуассона.

Если же (в пустоте), то уравнение Пуассона принимает вид:

-уравнение Лапласа.

получаем, что функция 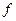должна удовлетворять уравнению:

3.Калибровка поперечных волн

Полагаем 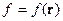есть функция только координат.

Значит функция 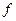должна удовлетворять уравнению: