Схема исследования функции на выпуклость и точки перегиба.

1. Найти ОДЗ функции .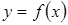

2. Найти вторую производную функции .

3. Найти точки, в которых вторая производная или не существует.

4. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.

5. Найти значения функции в точках перегиба.

Пример.

Найти интервалы выпуклости и точки перегиба графика функции .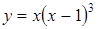

Решение.

1. ОДЗ: .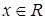

2. (см. пример №3).

.

3. Т.е. при и .

+ – +

1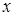

4. на интервалах и , следовательно, на этих интервалах функция вогнута.

на интервале . Следовательно, функция на нем выпукла.

5. и есть точки перегиба.

Асимптоты графика функции

Определение.

Асимптотой графика функции 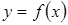называется прямая, обладающая тем свойством, что расстояние от точки , лежащей на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки графика от начала координат.

Различают три вида асимптот: вертикальные, горизонтальные, наклонные.

1. Вертикальные.

Если при , то - вертикальная асимптота.

Вертикальные асимптоты следует искать в точках разрыва функции .

2. Наклонные.

Прямая является наклонной асимптотой графика функции , если существуют конечные пределы:

, .

3. Горизонтальные.

Горизонтальные асимптоты – частный случай наклонных .

Пример.

Найти асимптоты кривой .

Решение.

Функция определена в интервалах , а и -точки разрыва. Так как , то прямая является вертикальной асимптотой кривой; , т.е. прямая не является вертикальной асимптотой. Горизонтальных асимптот кривая не имеет, так как и не являются конечными величинами. Определим, существуют ли наклонные асимптоты.

Находим:

;

.

Таким образом, существует правая наклонная асимптота .

Аналогично находятся:

;

.

Итак, существует наклонная асимптота .

Общая схема исследования функций и построения их графиков

1. Найти область определения функции и точки разрыва.

2. Исследовать функцию на четность ( ) – нечетность ( ), периодичность ( ).

3. Найти точки пересечения графика функции с осью и если это несложно – с осью .

4. Найти асимптоты кривой.

5. Найти интервалы возрастания и убывания функции и ее экстремумы.

6. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.

7. На основе проверенного анализа построить график функции.

Пример.

Исследовать функцию 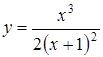и построить ее график.

Решение.

1. Область определения , т.е. . Точка – точка разрыва.

2. Четность, нечетность, периодичность:

.

Значит, функция не является ни четной, ни нечетной; и не является периодичной, т.к. нет такого Т, чтобы выполнилось равенство .

3. График функции проходит через начало координат.

4. Так как – точка разрыва, найдем предел функции при :

Таким образом, прямая является вертикальной асимптотой.

Проверим, имеет ли кривая наклонные асимптоты:

.

.

Т.о., прямая - наклонная асимптота.

Горизонтальных асимптот нет.

5. Экстремумы и интервалы монотонности. Найдем:

.

Производная обращается в ноль, если , т.е. при ; производная не существует при .

Однако критическими точками являются только точки (так как значение не входит в область определения функции).

Поскольку при , а при , то - точка максимума и - максимум функции ( - точка разрыва, т. е. в ней функция не может иметь экстремума).

На интервале функция убывает, на интервалах - возрастает.

6. Интервалы выпуклости и точки перегиба. Найдем:

.

Вторая производная обращается в ноль при х=0 и не существует при х=-1. Очевидно, что на интервале и функция вогнута на этом интервале на интервалах , и на этих интервалах функция выпукла. Точкой перегиба является .

7. По данным исследований строим график:

-3 -1 0 2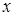

ІІІ. Интегральное исчисление