Классическое определение вероятности

1. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 2 очка, равна…
a) 0,2
b)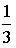
c)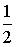
d)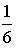

2. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 3 очка, равна…
a) 0,1
b)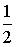
c)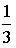
d)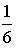

3. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 4 очка, равна…
a) 0,2
b)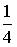
c)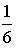
d)

4. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 6 очков, равна…
a)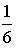
b) 1
c) 0,1
d) 0

5. Из урны, в которой находятся 4 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
a)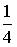
b)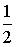
c)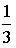
d) 1

6. Из урны, в которой находятся 4 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
a)
b) 1
c)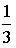
d)

7. Из урны, в которой находятся 4 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
a)
b) 1
c)
d)

8. Из урны, в которой находятся 5 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
a)
b) 1
c)
d)

9. Из урны, в которой находятся 5 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
a) 1
b)
c)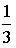
d)

10. Из урны, в которой находятся 5 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
a)
b)
c)
d) 1

Коэффициенты эластичности

1. Для мультипликативной производственной функции коэффициент эластичности по капиталу равен …
a) 0,51
b) 3,11
c) 0,6
d) 1,11

2. Для мультипликативной производственной функции коэффициент эластичности по капиталу равен …
a) 1,1
b) 0,59
c) 0,51
d) 3,1

3. Для мультипликативной производственной функции коэффициент эластичности по капиталу равен …
a) 0,52
b) 0,59
c) 3,11
d) 1,11

4. Для мультипликативной производственной функции коэффициент эластичности по капиталу равен …
a) 1,1
b) 0,58
c) 0,52
d) 3,1

5. Для мультипликативной производственной функции коэффициент эластичности по капиталу равен …
a) 0,59
b) 0,57
c) 3,16
d) 1,16

6. Для мультипликативной производственной функции коэффициент эластичности по труду равен …
a) 1,22
b) 0,62
c) 0,6
d) 3,22

7. Для мультипликативной производственной функции коэффициент эластичности по труду равен …
a) 1,21
b) 0,59
c) 3,21
d) 0,62

8. Для мультипликативной производственной функции коэффициент эластичности по труду равен …
a) 1,23
b) 0,64
c) 0,59
d) 3,23

9. Для мультипликативной производственной функции коэффициент эластичности по труду равен …
a) 3,21
b) 0,57
c) 1,21
d) 0,64

10. Для мультипликативной производственной функции коэффициент эластичности по труду равен …
a) 0,62
b) 3,17
c) 0,55
d) 1,17

Кривые второго порядка

1. Радиус окружности, заданной уравнением , равен…
a) 1
b) 4
c) – 2
d) 2

2. Радиус окружности, заданной уравнением , равен…
a) 9
b) – 3
c) 3
d) 6

3. Радиус окружности, заданной уравнением , равен…
a) 8
b) 16
c) 4
d) – 4

4. Радиус окружности, заданной уравнением , равен…
a) – 3
b) 6
c) 3
d) 9

5. Радиус окружности, заданной уравнением , равен…
a) 4
b) 6
c) 3
d) – 3

6. Радиус окружности, заданной уравнением , равен…
a) – 3
b) 2
c) 6
d) 3

7. Радиус окружности, заданной уравнением , равен…
a) 8
b) 4
c) – 4
d) 5

8. Радиус окружности, заданной уравнением , равен…
a) 3
b) 8
c) 4
d) – 4

9. Радиус окружности, заданной уравнением , равен…
a) 10
b) 4
c) 5
d) – 5

10. Радиус окружности, заданной уравнением , равен…
a) 6
b) 5
c) 10
d) – 5

Линейное программирование_ аналитическое задание области допустимых решений

1. Максимальное значение целевой функции при ограничениях

равно:
a) 10
b) 11
c) 8
d) 6

2. Максимальное значение целевой функции при ограничениях

равно:
a) 16
b) 6
c) 14
d) 10

3. Максимальное значение целевой функции при ограничениях

равно:
a) 6
b) 12
c) 18
d) 20

4. Максимальное значение целевой функции при ограничениях

равно:
a) 6
b) 26
c) 28
d) 16

5. Максимальное значение целевой функции при ограничениях

равно:
a) 18
b) 12
c) 14
d) 16

6. Максимальное значение целевой функции при ограничениях

равно:
a) 12
b) 28
c) 30
d) 20

7. Максимальное значение целевой функции при ограничениях

равно:
a) 20
b) 16
c) 12
d) 22

8. Максимальное значение целевой функции при ограничениях

равно:
a) 24
b) 20
c) 18
d) 22

9. Максимальное значение целевой функции при ограничениях

равно:
a) 6
b) 22
c) 14
d) 23

10. Максимальное значение целевой функции при ограничениях

равно:
a) 24
b) 26
c) 12
d) 18

Линейное программирование_ графическое задание области допустимых решений

1. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 18
b) 12
c) 20
d) 17

2. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 22
b) 24
c) 20
d) 16

3. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 20
b) 23
c) 26
d) 28

4. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 18
b) 23
c) 21
d) 20

5. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 25
b) 27
c) 24
d) 16

6. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции z=3x₁+5x₂ равно…
a) 29
b) 31
c) 20
d) 27

7. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 30
b) 24
c) 26
d) 28

8. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 20
b) 34
c) 32
d) 27

9. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 30
b) 32
c) 26
d) 24

10. Область допустимых решений задачи линейного программирования имеет вид:

Тогда максимальное значение функции равно…
a) 31
b) 25
c) 33
d) 28