Теоремы о предельном переходе
12.24. Если переменная 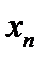 (последовательность
(последовательность 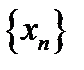 ) имеет конечны предел, то для любого действительного имеет место равенство
) имеет конечны предел, то для любого действительного имеет место равенство
(12.1) 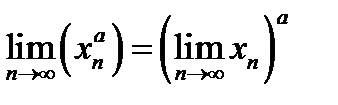
в предположении, что степени 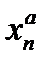 и
и 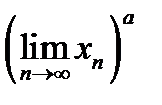 имеют смысл. Короче: можно переходить к пределу в основании степени с любым действительным показателем.
имеют смысл. Короче: можно переходить к пределу в основании степени с любым действительным показателем.
12.25. Если переменная 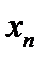 имеет конечный предел, то имеет место формула
имеет конечный предел, то имеет место формула
(12.2) 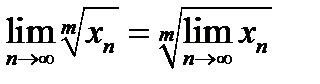
т.е.можно переходить к пределу под знаком корня (в случае четного 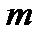 предполагается, что
предполагается, что 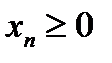 и корень берется арифметический.
и корень берется арифметический.
12.26. Если 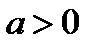 , а
, а 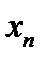 принимает только положительные значения и имеет предел, не равный нулю, то имеет место формула
принимает только положительные значения и имеет предел, не равный нулю, то имеет место формула
(12.3) 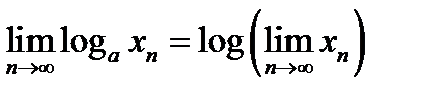
Короче: можно переходить к пределу под знаком логарифма.
12.27. Если 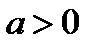 , а переменная
, а переменная 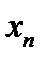 имеет конечный предел, то имеет место формула
имеет конечный предел, то имеет место формула
(12.4) 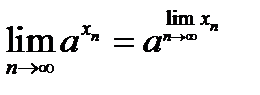
Короче: при фиксированном основании можно переходить к пределу в показатели степени.
Теперь приступим к решению типовых задач на отыскание предела переменной 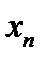 (предела последовательности
(предела последовательности 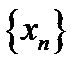 ).
).
Задача 12.1
Найти предел переменной.
(12.5) 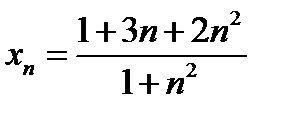
Последовательность 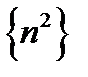 расходится к
расходится к 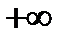 , а значит и последовательность
, а значит и последовательность 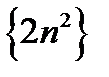 расходиться к
расходиться к 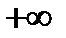 (п. 12.22). На том же основании последовательность
(п. 12.22). На том же основании последовательность 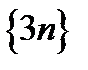 расходится к
расходится к 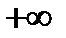 , а потому последовательность
, а потому последовательность 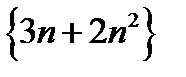 расходится к
расходится к 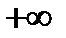 и на основании п.12.19 последовательность
и на основании п.12.19 последовательность 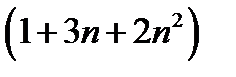 также расходиться к
также расходиться к 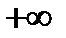 и
и 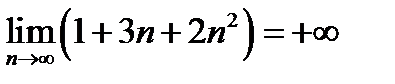 . Можно было рассуждать и иначе: при
. Можно было рассуждать и иначе: при 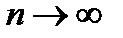 величина
величина 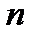 - бесконечно большая, ее квадрат, как произведение бесконечно больших величин, есть величина бесконечно большая (п. 12.13). На основании п.12.12 произведение
- бесконечно большая, ее квадрат, как произведение бесконечно больших величин, есть величина бесконечно большая (п. 12.13). На основании п.12.12 произведение 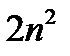 есть бесконечно большая величина, как произведение постоянной, не равной нулю, на бесконечно большую величину.
есть бесконечно большая величина, как произведение постоянной, не равной нулю, на бесконечно большую величину.
На том же основании величина 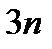 - бесконечно большая. Так как
- бесконечно большая. Так как 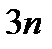 и
и 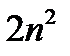 - бесконечно большие одного и того же знака, то и сумма их
- бесконечно большие одного и того же знака, то и сумма их 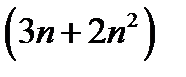 есть величина бесконечно большая того же знака, потому и
есть величина бесконечно большая того же знака, потому и 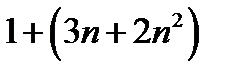 - бесконечно большая величина, как сумма постоянной величины 1 с бесконечно большой и снова
- бесконечно большая величина, как сумма постоянной величины 1 с бесконечно большой и снова 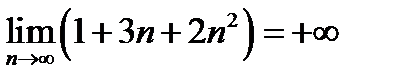 . Что касается знаменателя
. Что касается знаменателя 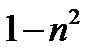 , при
, при 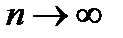 последовательность
последовательность 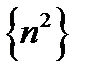 расходится к
расходится к 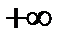 , и на основании п.12.19, б получаем, что последовательность
, и на основании п.12.19, б получаем, что последовательность 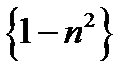 расходится к
расходится к 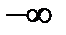 и знаменатель дроби (12.5) – тоже бесконечно большая величина.
и знаменатель дроби (12.5) – тоже бесконечно большая величина.
Таким образом, дробь (11.5) есть отношение двух бесконечно больших величин, о котором без исследования ничего определенного сказать нельзя. Здесь также нельзя применить теорему о пределе частного, так как в условии этой теоремы предполагается, что пределы числителя и знаменателя существуют, а в нашем случае ни числитель, ни знаменатель дроби предела не имеют (см. п. 12.9). Данную переменную (12.5) преобразуем, чтобы к ней можно было применить теоремы о пределах. Обыкновенно в этом случае поступают так: числитель и знаменатель дроби делят на наивысшую степень 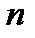 , встречающуюся в членах дроби [6].Тогда
, встречающуюся в членах дроби [6].Тогда
(12.6) 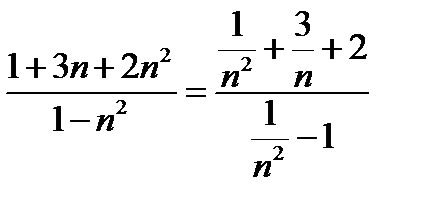
Отыскивая теперь предел последней дроби, мы сможем применить теорему о пределе частного, так как теперь числитель и знаменатель дроби имеют пределы: величины 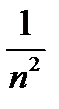 и
и 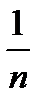 есть величины бесконечно малые, как величины обратные бесконечно большим
есть величины бесконечно малые, как величины обратные бесконечно большим 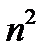 и
и 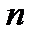 , а потому
, а потому
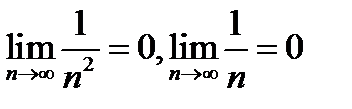 .
.
Величина 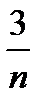 есть тоже бесконечно малая, как произведение постоянной величины 3 на бесконечно малую
есть тоже бесконечно малая, как произведение постоянной величины 3 на бесконечно малую 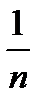 и
и 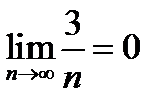 (п. 12 4А), и тогда существует предел числителя:
(п. 12 4А), и тогда существует предел числителя:
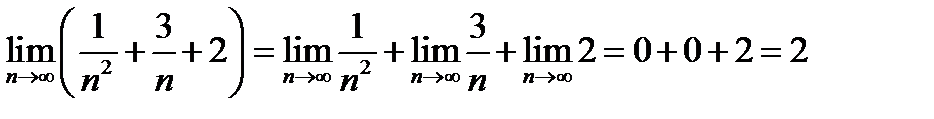
(предел постоянной величины 2 равен ей самой).
Предел знаменателя 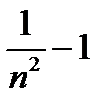 дроби (12.6) также существует и равен -1, так как
дроби (12.6) также существует и равен -1, так как
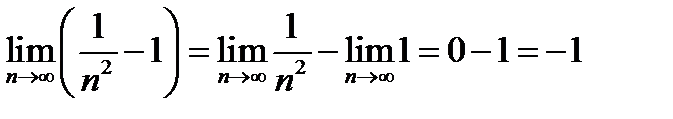 ;
; 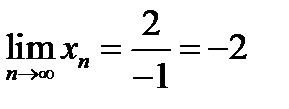 .
.
После этих подробных рассуждений укажем, как следует расположить записи:
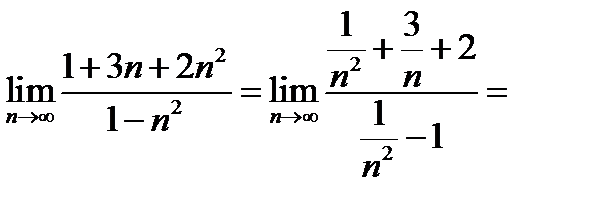
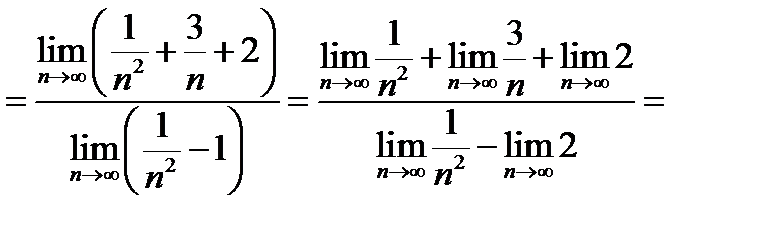
(здесь применена теорема о пределе дроби. Это можно было сделать только после, того, как мы убедились, что существуют пределы числителя и знаменателя).
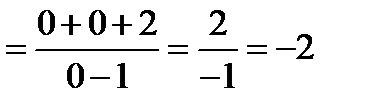 .
.
Такие подробные записи в последующем, когда выработается определенный навык, можно сократить.
Задача 12.2
Найти 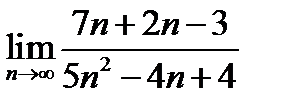 .
.
Решение.
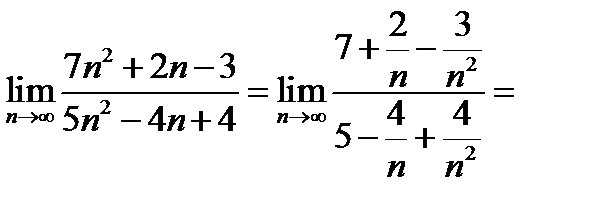
(числитель и знаменатель данной дроби разделен на 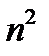 )
)
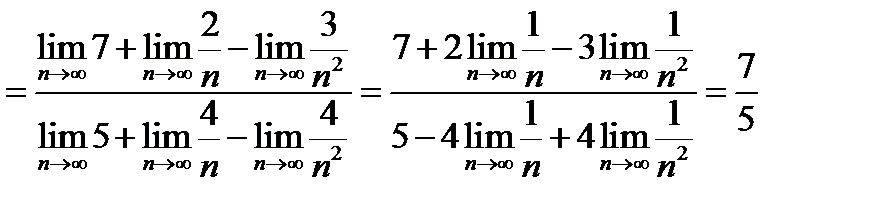 .
.
(применена теорема о пределе дроби).
Задача 12.3
(для самостоятельного решения).Найти:
1) 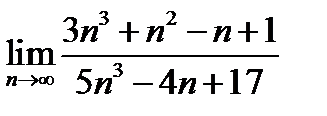 ;
;
2) 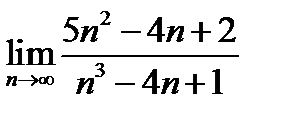 ;
;
Ответ.
1) 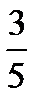 ;
;
2) 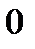 .
.
Задача 12.4
(для самостоятельного решения). Найти 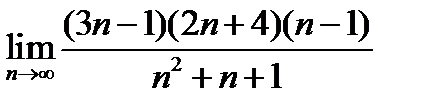 .
.
Ответ.
Последовательность расходиться к 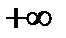 . Можно употребить символическую запись и написать что
. Можно употребить символическую запись и написать что
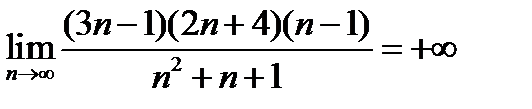 .
.
Указание. В числителе перемножить двучлены, разделить числитель и знаменатель на 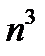 и воспользоваться п.12.23.
и воспользоваться п.12.23.
Задача 12.5
(для самостоятельного решения). Найти предел переменной 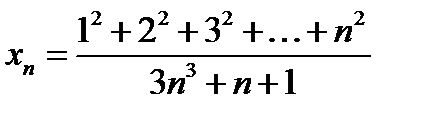 .
.
Указание. Известно, что сумма квадратов чисел натурального ряда 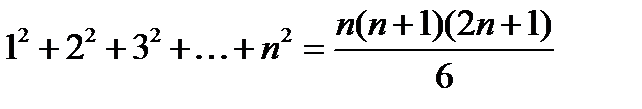 .
.
Ответ. 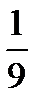 .
.
Задача 12.6
(для самостоятельного решения). Найти
1) 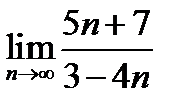 ;
;
2) 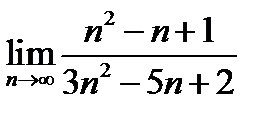 ;
;
3) 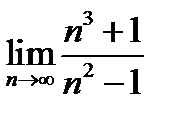 ;
;
4) 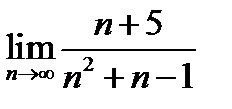 .
.
Ответ.
1) 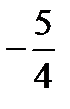 ;
;
2) 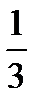 ;
;
3)  ;
;
4) 0.
Задача 12.7
Доказать, что если 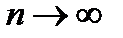 , то 1)
, то 1) 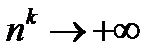 , когда
, когда 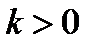 ; 2)
; 2) 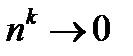 , когда
, когда 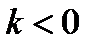 ; 3)
; 3) 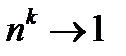 , когда
, когда 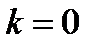 .
.
Решение.
1) Пусть 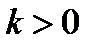 , а
, а 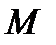 - любое заданное положительное число.
- любое заданное положительное число.
Чтобы доказать, что 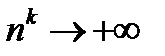 мы должны показать, что можно найти такое натуральное число
мы должны показать, что можно найти такое натуральное число 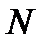 , что
, что 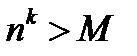 при
при 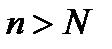 .
.
Так как 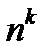 должно быть большим, чем
должно быть большим, чем 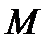 , то это равносильно тому, что должно быть
, то это равносильно тому, что должно быть 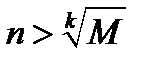 , и за
, и за 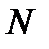 можно принять
можно принять 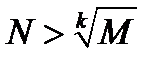 ; тем самым доказано, что
; тем самым доказано, что 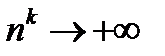 при
при 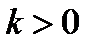 . Например, если
. Например, если 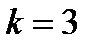 , а
, а 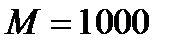 , то должно выполняться неравенство
, то должно выполняться неравенство 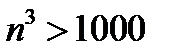 для вех
для вех 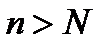 причем следует взять
причем следует взять 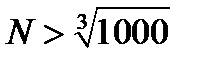 , т.е. принять
, т.е. принять 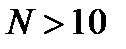 . Значит, начиная с
. Значит, начиная с 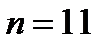 , неравенство
, неравенство 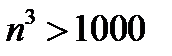 будет выполняться.
будет выполняться.
Если взять 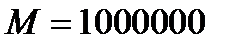 , то должно выполняться неравенство
, то должно выполняться неравенство 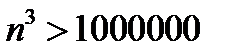 для всех
для всех 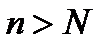 , и следует взять
, и следует взять 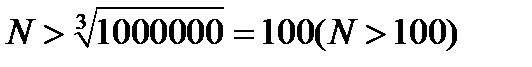 и при
и при 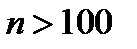 , т.е. начиная с
, т.е. начиная с 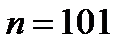 неравенство
неравенство 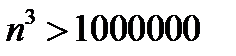 будет выполняться.
будет выполняться.
Доказательство пунктов 2) и 3) предоставляется читателю. При доказательстве п.2) и 3) выгодно взять 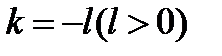 , и тогда
, и тогда 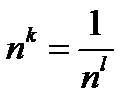 ; при доказательстве п.3) учесть, что если
; при доказательстве п.3) учесть, что если 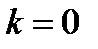 , то всегда
, то всегда 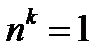 при любом
при любом 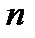 .
.
Результат проведенных вычислений можно записать и так:
(12.7) 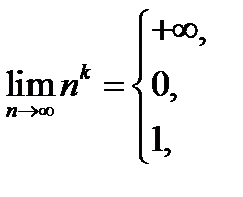
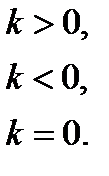
В задачах 12.1-12.6 мы рассматривали пределы отношения двух целых рациональных функций от 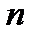 в частных случаях. После решения предыдущей задачи мы можем рассмотреть вопрос об отношении двух целых рациональных функций в общем виде.
в частных случаях. После решения предыдущей задачи мы можем рассмотреть вопрос об отношении двух целых рациональных функций в общем виде.
Задача 12.8
Найти предел при 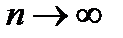
(12.8) 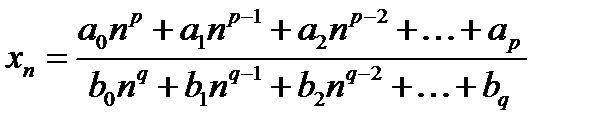
причем 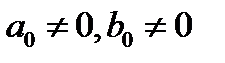 .
.
Решение.
Перепишем (12.8) в виде
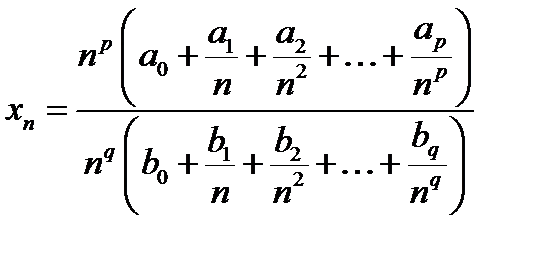 ;
;
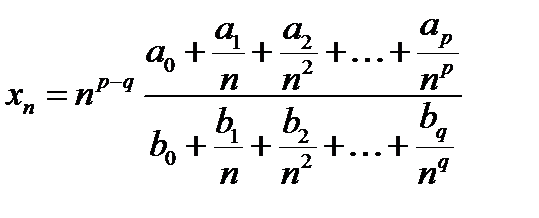
Тога предел
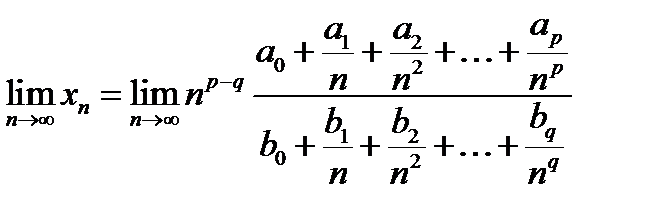 .
.
Предел второго сомножителя равен 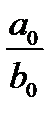 , так как в числителе и знаменателе предел каждого слагаемого, кроме первых (
, так как в числителе и знаменателе предел каждого слагаемого, кроме первых ( 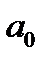 и
и 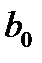 ), равен нулю. Что касается первого сомножителя, то его предел зависит от знака разности
), равен нулю. Что касается первого сомножителя, то его предел зависит от знака разности 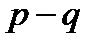 :
:
1) Если 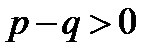 , т.е.
, т.е. 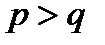 , то на основании (12.7)
, то на основании (12.7) 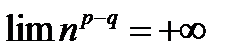 , и тогда, в соответствии с п.12.22, заключаем, что
, и тогда, в соответствии с п.12.22, заключаем, что 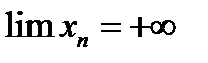 .
.
2) Если 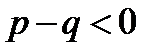 , т.е.
, т.е. 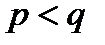 , то из (12.7) следует, что
, то из (12.7) следует, что 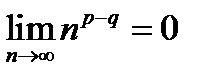 ; тогда искомый предел равен нулю:
; тогда искомый предел равен нулю: 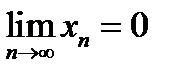 .
.
3) Если же 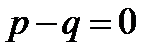 , т.е.
, т.е. 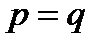 , то
, то 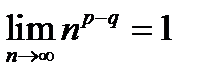 или
или 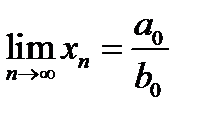 . Соединяя полученные результаты, приходим к выводу, что
. Соединяя полученные результаты, приходим к выводу, что
(12.9) 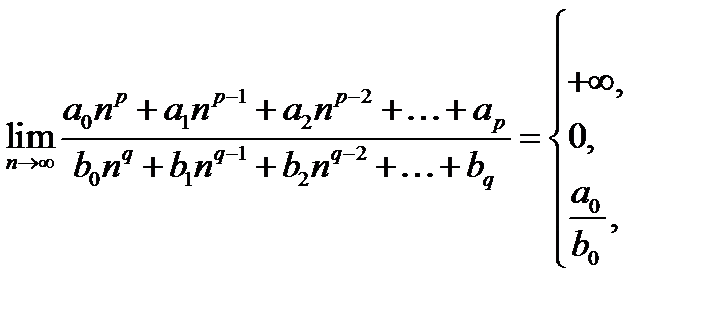
Таким образом, при 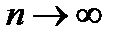 предел отношения двух целых рациональных функций от
предел отношения двух целых рациональных функций от 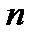 равен
равен
1) Отношению коэффициентов при высших степенях 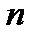 , если степени этих функций между собою равны;
, если степени этих функций между собою равны;
2) Нулю, если степень числителя меньше степени знаменателя и
3) 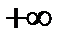 , если степень числителя больше степени знаменателя.
, если степень числителя больше степени знаменателя.
Заключения, полученные при решении задач 12.1-12.6, совпадают с только сто сделанными.
Задача 12.9
Найти 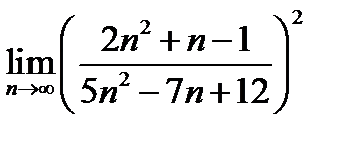
Решение.
Воспользуемся указанием п. 12.24, заметив, что основание степени имеет предел
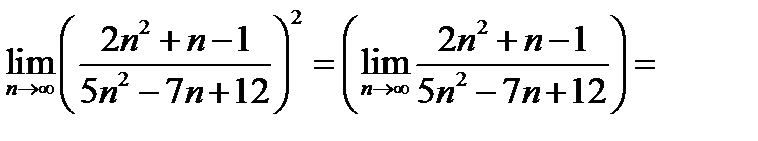
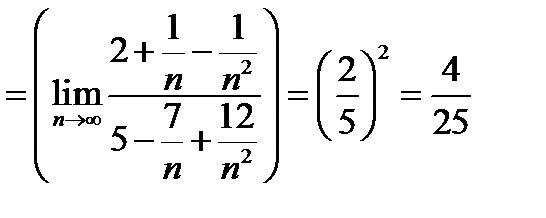 .
.
Задача 12.10
(для самостоятельного решения). Найти 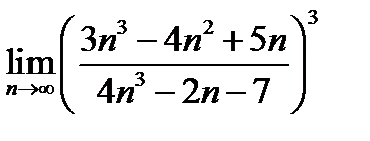 .
.
Ответ. 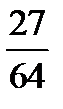 .
.
Задача 12.11
Найти 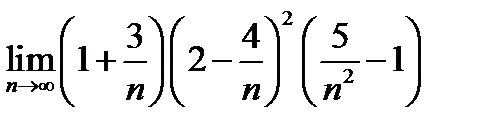 .
.
Решение.
Применяя теорему о пределе произведения (это мы имеем право сделать, так как каждый сомножитель имеет предел) получаем последовательно:
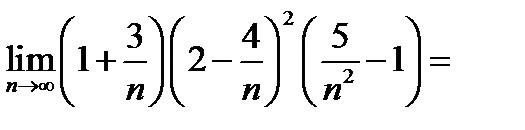
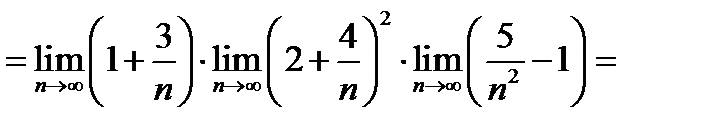
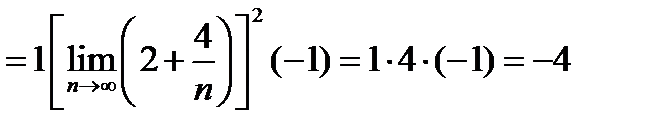 .
.
Т.к. 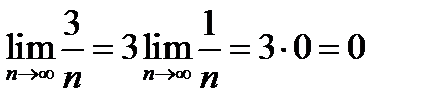 , ибо если
, ибо если 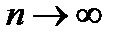 , то величина ей обратная
, то величина ей обратная 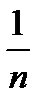 - бесконечна мала
- бесконечна мала 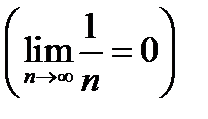 .
.
Задача 12.12
Найти 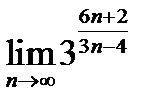 .
.
Решение.
Воспользуемся указанием п.12.27 о переходе к пределу в показателе степени 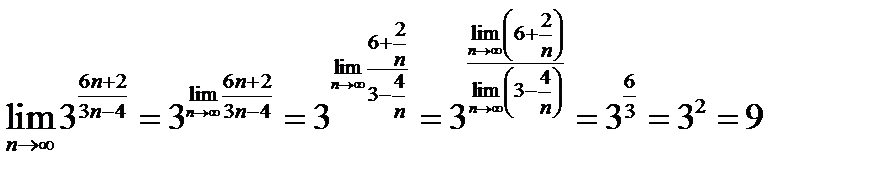 .
.
Задача 12.13
(для самостоятельного решения). Найти:
1) 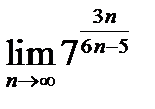 ;
;
2) 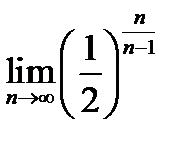 ;
;
3) 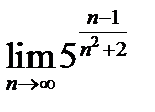 .
.
Ответ.
1) 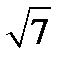 ;
;
2) 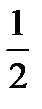 ;
;
3) 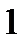 .
.
Задача 12.14
Найти 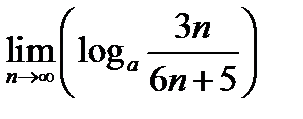 .
.
Решение.
На основании формулы (12.3), допускающей переход к пределу под знаком логарифма, имеем:
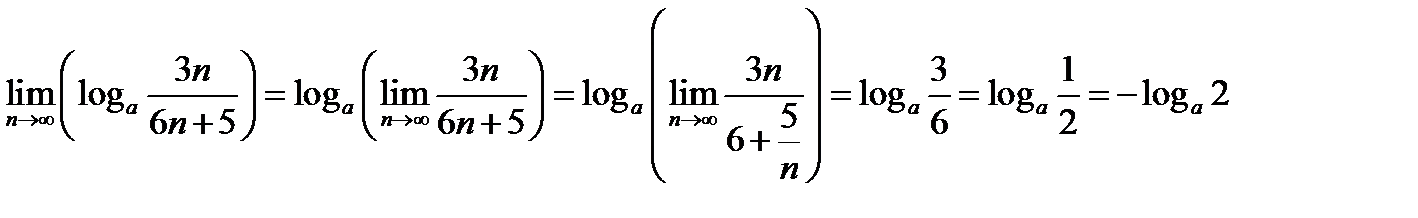
Задача 12.15
(для самостоятельного решения). Найти:
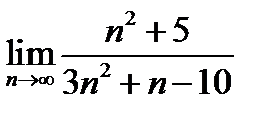 .
.
Ответ. 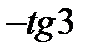 .
.
ЧЕТЫРНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Предел функции.
