Критические значения критерия Колмогорова-Смирнова
| α | 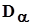 | |||
| 0.2 | 0.208 | 0.148 | 0.118 | 0.106 |
| 0.1 | 0.238 | 0.169 | 0.135 | 0.121 |
| 0.05 | 0.264 | 0.188 | 0.150 | 0.134 |
Если n > 10и вероятность a выражена в относительных единицах, для расчета критических значений можно пользоваться приближенной формулой
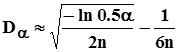 .
.
Процедура проверки гипотезы о виде функции распределения по критерию Колмогорова - Смирнова.
1. Задается уровень значимости a.
2. По выборочным данным строится выборочная функция распределения в соответствии с указаниями п. 2.2
3. Вычисляются точечные оценки моментов.
4. Из теоретических соображений, по виду выборочной функции распределения, по соотношениям между моментами, по значениям асимметрии и эксцесса, по другим соображениям выдвигается гипотеза о виде функции распределения 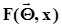 и тем самым - о виде плотности распределения
и тем самым - о виде плотности распределения 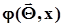 .
.
5. Вычисляется r параметров предполагаемой функции распределения и ее значения 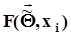 при
при 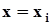 .
.
6. Вычисляется статистика критерия 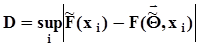
7. Полученное значение сравнивается с критическим значением 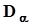 .
.
8. Если 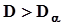 делается вывод о том, что экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или о том, что отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза, переход на п. 4 настоящей процедуры.
делается вывод о том, что экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или о том, что отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза, переход на п. 4 настоящей процедуры.
9. Если 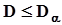 делается вывод о том, что экспериментальные данные не противоречат выдвинутой гипотезе или о том, что имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.
делается вывод о том, что экспериментальные данные не противоречат выдвинутой гипотезе или о том, что имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.
47. Проверка гипотез о виде плотности распределения по критерию “омега-квадрат” Мизеса. Из генеральной совокупности X ,образованной случайной величиной x, извлечена выборка 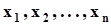 . Выдвигается предположение, что ф-я распределения случайной величины -
. Выдвигается предположение, что ф-я распределения случайной величины - 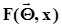 ,
, 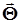 - вектор параметров. По выборочным данным вычисляются оценки параметров
- вектор параметров. По выборочным данным вычисляются оценки параметров 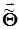 и проверяется гипотеза
и проверяется гипотеза  : функция распределения случайной величины x есть
: функция распределения случайной величины x есть 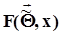 против альтернативы
против альтернативы 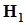 : функция распределения случайной величины x не
: функция распределения случайной величины x не 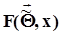 .Поскольку эта гипотеза сложная, задается только вероятность ошибки первого рода a -уровень значимости.В соответствии с формулировкой гипотезы сравниваются две функции распределения: выборочная и предполагаемая. Различие между ними
.Поскольку эта гипотеза сложная, задается только вероятность ошибки первого рода a -уровень значимости.В соответствии с формулировкой гипотезы сравниваются две функции распределения: выборочная и предполагаемая. Различие между ними 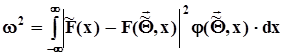 ,
, 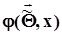 - предполагаемая плотность распределения.Этот интеграл = сумма инт-ов по интервалам между соседними членами вариационного ряда. Если на этих интервалах предполагаемая функция распределения интерполируется прямой линией, то этот интеграл выражается суммой
- предполагаемая плотность распределения.Этот интеграл = сумма инт-ов по интервалам между соседними членами вариационного ряда. Если на этих интервалах предполагаемая функция распределения интерполируется прямой линией, то этот интеграл выражается суммой 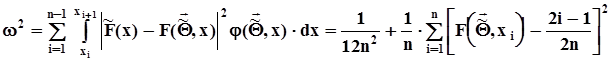
В качестве статистики критерия используется 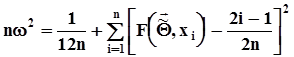
Критические значения 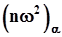 .В таблице приводятся некоторые часто употребляемые критические значения. Критические значения критерия
.В таблице приводятся некоторые часто употребляемые критические значения. Критические значения критерия 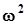 Мизеса.
Мизеса.
| a | 0.03 | 0.05 | 0.1 | 0.2 |
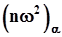 | 0.55 | 0.4614 | 0.3473 | 0.2415 |
Процедура проверки гипотезы о виде функции распределения по критерию 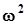 Мизеса. 1. Задается уровень значимости a2. строится выборочная функция распределения. 3. Вычисляются точечные оценки моментов.4. Из теоретических соображений, по виду выборочной функции распределения, по соотношениям между моментами, по значениям асимметрии и эксцесса, по другим соображениям выдвигается гипотеза о виде функции распределения
Мизеса. 1. Задается уровень значимости a2. строится выборочная функция распределения. 3. Вычисляются точечные оценки моментов.4. Из теоретических соображений, по виду выборочной функции распределения, по соотношениям между моментами, по значениям асимметрии и эксцесса, по другим соображениям выдвигается гипотеза о виде функции распределения 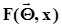 и о виде плотности распределения
и о виде плотности распределения 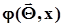 .5. Вычисляется r параметров предполагаемой функции распределения и ее значения
.5. Вычисляется r параметров предполагаемой функции распределения и ее значения 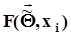 при
при 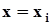 .6. Вычисляется статистика критерия
.6. Вычисляется статистика критерия 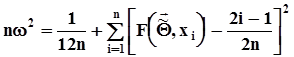 7. Полученное значение сравнивается с критическим значением
7. Полученное значение сравнивается с критическим значением 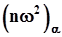 .8. Если
.8. Если 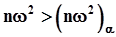 ,то экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза, переход на п. 4 настоящей процедуры.9. Если
,то экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза, переход на п. 4 настоящей процедуры.9. Если 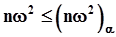 ,то экспериментальные данные подтверждают справедливость выдвинутой гипотезы имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.Критерий
,то экспериментальные данные подтверждают справедливость выдвинутой гипотезы имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.Критерий 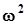 Мизеса - равномерно наиболее мощный критерий проверки гипотезы о виде функции распределения.
Мизеса - равномерно наиболее мощный критерий проверки гипотезы о виде функции распределения.
48. Проверка сложных гипотез о математическом ожидании с применением фидуциальных вероятностей и контролем вероятностей ошибок первого и второго рода. Плотность распределения генеральной совокупности X - нормальна, дисперсия неизвестна. Из генеральной совокупности извлечена выборка 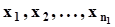 объема
объема 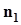 .
.  :
: 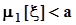 против альтернативы
против альтернативы 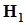 :
: 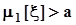 .Заданы вероятности ошибок 1го и 2го рода a и b.Естественной статистикой для проверки гипотезы о математическом ожидании, как и ранее, является среднее арифметическое значение выборочных данных, а для построения доверительного интервала для математического ожидания требуется вычислить оценку дисперсии:
.Заданы вероятности ошибок 1го и 2го рода a и b.Естественной статистикой для проверки гипотезы о математическом ожидании, как и ранее, является среднее арифметическое значение выборочных данных, а для построения доверительного интервала для математического ожидания требуется вычислить оценку дисперсии: 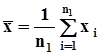 .
. 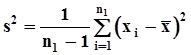 .Доверительный интервал для математического ожидания строится с помощью коэффициентов Стъюдента
.Доверительный интервал для математического ожидания строится с помощью коэффициентов Стъюдента 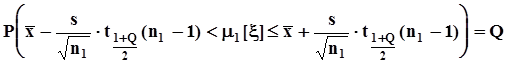 .Эту вероятность Фишер предложил трактовать, как вероятностную меру полуоткрытого интервала
.Эту вероятность Фишер предложил трактовать, как вероятностную меру полуоткрытого интервала 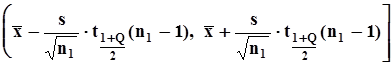 , из чего сразу же следует трактовка генеральной характеристики - математического ожидания
, из чего сразу же следует трактовка генеральной характеристики - математического ожидания 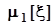 , как случайной величины, каковое заключение как раз является основной причиной неполного признания такой вероятностной меры, которую Фишер назвал фидуциальной.Посмотрим, как, несмотря ни на что, применить эту меру с пользой для дела, а именно, для проверки сформулированной гипотезы с контролем вероятностей a и b. На рис. 38 показаны три варианта возможного расположения этого доверительного интервала относительно границы а, которая разделяет вещественную ось на две зоны, соответствующие гипотезам
, как случайной величины, каковое заключение как раз является основной причиной неполного признания такой вероятностной меры, которую Фишер назвал фидуциальной.Посмотрим, как, несмотря ни на что, применить эту меру с пользой для дела, а именно, для проверки сформулированной гипотезы с контролем вероятностей a и b. На рис. 38 показаны три варианта возможного расположения этого доверительного интервала относительно границы а, которая разделяет вещественную ось на две зоны, соответствующие гипотезам  и
и 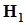 .В соответствии с формулировкой гипотезы положение нижней границы доверительного интервала в зоне, соответствующей гипотезе
.В соответствии с формулировкой гипотезы положение нижней границы доверительного интервала в зоне, соответствующей гипотезе  , безразлично, и поэтому на рис. 38 а) нижняя граница обозначена условно. По указанной причине для этого варианта строится доверительный интервал, нижняя граница которого равна - ¥, а верхняя граница определяется заданной вероятностью b ошибки второго рода :
, безразлично, и поэтому на рис. 38 а) нижняя граница обозначена условно. По указанной причине для этого варианта строится доверительный интервал, нижняя граница которого равна - ¥, а верхняя граница определяется заданной вероятностью b ошибки второго рода : 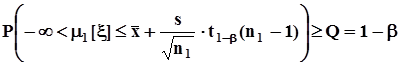 , где
, где 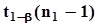 -
- 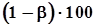 - процентная квантиль плотности распределения Стъюдента.Это равенство означает, что, с позиций фидуциальной вероятностной меры, истинное значение
- процентная квантиль плотности распределения Стъюдента.Это равенство означает, что, с позиций фидуциальной вероятностной меры, истинное значение 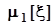 находится в зоне, соответствующей гипотезе
находится в зоне, соответствующей гипотезе  с вероятностью, не меньше, чем Q. В этой ситуации, когда
с вероятностью, не меньше, чем Q. В этой ситуации, когда 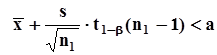 ,принимается решение о справедливости гипотезы
,принимается решение о справедливости гипотезы  . Вероятность ошибки в этом решении не будет превышать значения вероятности, с которой истинное значение
. Вероятность ошибки в этом решении не будет превышать значения вероятности, с которой истинное значение 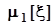 расположено справа от верхней границы доверительного интервала. Объясняется это тем, что здесь
расположено справа от верхней границы доверительного интервала. Объясняется это тем, что здесь 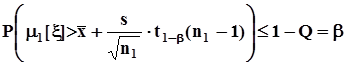 ,и в силу монотонности вероятностной меры
,и в силу монотонности вероятностной меры 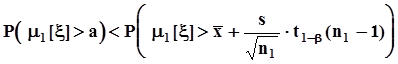 ,а это означает, что
,а это означает, что 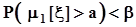 .Поэтому в показанной ситуации вероятность ошибочного решения о признании гипотезы
.Поэтому в показанной ситуации вероятность ошибочного решения о признании гипотезы  справедливой не превысит заданного значения b:
справедливой не превысит заданного значения b: 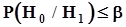 .Точно так же в соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе
.Точно так же в соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе 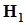 , безразлично. По указанной причине для этого варианта строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода :
, безразлично. По указанной причине для этого варианта строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода : 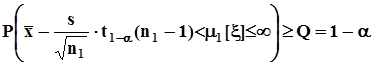 ,
, 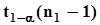 -
- 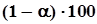 - процентная квантиль плотности распределения Стъюдента с .
- процентная квантиль плотности распределения Стъюдента с . 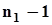 степенями свободы.Это равенство означает, что, с позиций фидуциальной вероятностной меры, истинное значение
степенями свободы.Это равенство означает, что, с позиций фидуциальной вероятностной меры, истинное значение 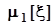 находится в зоне, соответствующей гипотезе
находится в зоне, соответствующей гипотезе 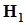 с вероятностью, не меньше, чем Q = 1 -
с вероятностью, не меньше, чем Q = 1 - 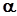 . В этой ситуации, когда
. В этой ситуации, когда 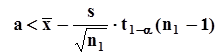 ,принимается решение о справедливости гипотезы
,принимается решение о справедливости гипотезы 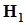 . Вероятность ошибки в этом решении не будет превышать значения вероятности, с которой истинное значение
. Вероятность ошибки в этом решении не будет превышать значения вероятности, с которой истинное значение 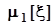 расположено слева от нижней границы доверительного интервала.Объясняется это тем, что здесь
расположено слева от нижней границы доверительного интервала.Объясняется это тем, что здесь 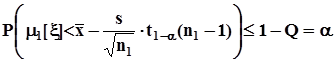 ,и в силу монотонности вероятностной меры
,и в силу монотонности вероятностной меры 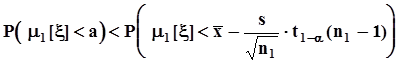 ,а это означает, что
,а это означает, что 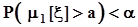 .Поэтому в показанной ситуации вероятность ошибочного решения о признании гипотезы
.Поэтому в показанной ситуации вероятность ошибочного решения о признании гипотезы 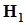 справедливой не превысит заданного значения a:
справедливой не превысит заданного значения a: 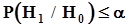 .В третьем варианте, показанном на рис. 38 с), у нас нет достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается. После увеличения объема выборки до
.В третьем варианте, показанном на рис. 38 с), у нас нет достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается. После увеличения объема выборки до 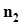 снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения а. Все описанные выше рассуждения и действия повторяются.
снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения а. Все описанные выше рассуждения и действия повторяются.
 В конечном итоге описанная последовательная процедура проверки сложной гипотезы о математическом ожидании должна завершиться выходом доверительного интервала целиком в одну из зон и принятием соответствующей гипотезы. В случаях, когда по экономическим, техническим и иным причинам дальнейшее продолжение испытаний оказывается невозможным, придется принимать произвольное решение об отклонении той или иной гипотезы в зависимости от того, риск какого рода (первого или второго) более оправдан. Второй разновидностью сложной гипотезы о математическом ожидании, которая имеет важные практические приложения, является гипотезаb)
В конечном итоге описанная последовательная процедура проверки сложной гипотезы о математическом ожидании должна завершиться выходом доверительного интервала целиком в одну из зон и принятием соответствующей гипотезы. В случаях, когда по экономическим, техническим и иным причинам дальнейшее продолжение испытаний оказывается невозможным, придется принимать произвольное решение об отклонении той или иной гипотезы в зависимости от того, риск какого рода (первого или второго) более оправдан. Второй разновидностью сложной гипотезы о математическом ожидании, которая имеет важные практические приложения, является гипотезаb)  :
: 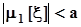 против
против 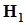 :
: 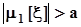 .К проверке такой гипотезы приходится прибегать, например, когда по результатам испытания продукции необходимо установить, что контролируемый параметр или параметры находятся в пределах установленного и рекламируемого допуска.Заданы вероятности ошибок 2го и 2го рода a и b, которые в этом случае приходится принимать равными, то есть a = b.4 по выборке объема
.К проверке такой гипотезы приходится прибегать, например, когда по результатам испытания продукции необходимо установить, что контролируемый параметр или параметры находятся в пределах установленного и рекламируемого допуска.Заданы вероятности ошибок 2го и 2го рода a и b, которые в этом случае приходится принимать равными, то есть a = b.4 по выборке объема 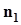 строится доверительный интервал
строится доверительный интервал 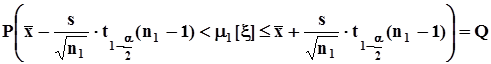 ,где на этот раз a = b,
,где на этот раз a = b, 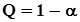 , и этот интервал располагается по отношению к интервалу
, и этот интервал располагается по отношению к интервалу 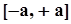 , соответствующему гипотезе
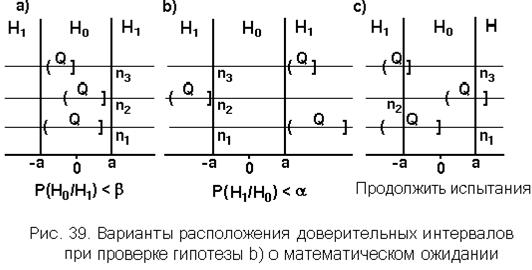
, соответствующему гипотезе  , как показано на рис. 39. Снова возможны три варианта расположения доверительного интервала.
, как показано на рис. 39. Снова возможны три варианта расположения доверительного интервала.
В первом варианте (рис. 39 а), когда доверительный интервал, который накрывает истинное значение 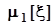 с вероятностью Q, целиком находится в зоне справедливости нулевой гипотезы, это означает, что истинное значение
с вероятностью Q, целиком находится в зоне справедливости нулевой гипотезы, это означает, что истинное значение 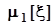 находится в зоне, соответствующей гипотезе
находится в зоне, соответствующей гипотезе  с вероятностью, превышающей Q. В этой ситуации принимается решение о принятии гипотезы
с вероятностью, превышающей Q. В этой ситуации принимается решение о принятии гипотезы  . Вероятность ошибочного решения не будет превышать b, то есть значения вероятности, с которой истинное значение
. Вероятность ошибочного решения не будет превышать b, то есть значения вероятности, с которой истинное значение 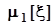 расположено вне доверительного интервала. Объясняется это тем, что в силу монотонности вероятностной меры в ситуации, показанной на рис. 39 а),
расположено вне доверительного интервала. Объясняется это тем, что в силу монотонности вероятностной меры в ситуации, показанной на рис. 39 а), 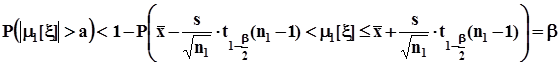 ,а это означает, что
,а это означает, что 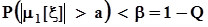 .Поэтому вероятность ошибочного решения о признании гипотезы
.Поэтому вероятность ошибочного решения о признании гипотезы  справедливой, то есть вероятность ошибки второго рода не превысит заданного значения b:
справедливой, то есть вероятность ошибки второго рода не превысит заданного значения b: 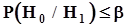 .Когда во втором варианте (рис. 39 b) доверительный интервал целиком находится вне зоны, соответствующей гипотезе
.Когда во втором варианте (рис. 39 b) доверительный интервал целиком находится вне зоны, соответствующей гипотезе  , справа или слева от нее, принимается решение о принятии гипотезы
, справа или слева от нее, принимается решение о принятии гипотезы 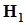 . Вероятность ошибочного решения не будет превышать α, то есть значения вероятности, с которой истинное значение
. Вероятность ошибочного решения не будет превышать α, то есть значения вероятности, с которой истинное значение 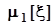 расположено вне доверительного интервала, поскольку в этой ситуации,- если доверительный интервал находится слева от зоны гипотезы
расположено вне доверительного интервала, поскольку в этой ситуации,- если доверительный интервал находится слева от зоны гипотезы  ,
, 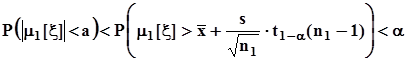 ,- если доверительный интервал находится справа от зоны гипотезы
,- если доверительный интервал находится справа от зоны гипотезы  , то также
, то также 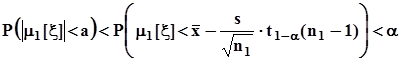 . Это означает, что
. Это означает, что 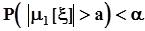 .
.
Поэтому вероятность ошибочного решения о признании гипотезы 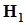 справедливой, то есть вероятность ошибки первого рода не превысит заданного значенияa:
справедливой, то есть вероятность ошибки первого рода не превысит заданного значенияa: 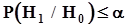 .В третьем варианте (рис. 39 с), как и прежде, принимается решение об увеличении объема выборки, если этому нет экономических, технических или иных препятствий. Получив выборку увеличенного объема
.В третьем варианте (рис. 39 с), как и прежде, принимается решение об увеличении объема выборки, если этому нет экономических, технических или иных препятствий. Получив выборку увеличенного объема 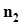 , процедуру повторяют до ее естественного завершения или до прекращения по соображениям экономического, технического или иного обоснованного характера.
, процедуру повторяют до ее естественного завершения или до прекращения по соображениям экономического, технического или иного обоснованного характера.
49. Проверка сложных гипотез о дисперсии с применением фидуциальных вероятностей и контролем вероятностей ошибок первого и второго рода.
Плотность распределения генеральной совокупности X - нормальна, дисперсия 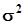 неизвестна. Из генеральной совокупности извлечена выборка
неизвестна. Из генеральной совокупности извлечена выборка 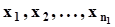 объема
объема 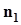 . Проверяется сложная гипотеза
. Проверяется сложная гипотеза  :
: 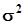 £d против альтернативы
£d против альтернативы 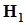 :
: 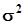 >d.Заданы вероятности ошибок первого и второго рода a и b.Естественной статистикой для проверки гипотезы о дисперсии является ее несмещенная оценка:
>d.Заданы вероятности ошибок первого и второго рода a и b.Естественной статистикой для проверки гипотезы о дисперсии является ее несмещенная оценка: 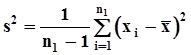 .Доверительный интервал для дисперсии определен следующим образом:
.Доверительный интервал для дисперсии определен следующим образом: 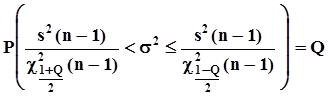 .На рис. 40 показаны варианты расположения доверительного интервала для дисперсии относительно зон, соответствующих гипотезам
.На рис. 40 показаны варианты расположения доверительного интервала для дисперсии относительно зон, соответствующих гипотезам  и
и 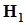 . В соответствии с формулировкой гипотезы и в связи с тем, что
. В соответствии с формулировкой гипотезы и в связи с тем, что 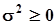 , положение нижней границы доверительного интервала в зоне, соответствующей гипотезе
, положение нижней границы доверительного интервала в зоне, соответствующей гипотезе  , безразлично. По указанным причинам для этого варианта строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью b ошибки второго рода :
, безразлично. По указанным причинам для этого варианта строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью b ошибки второго рода : 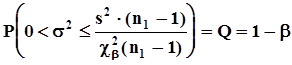 где
где 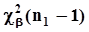 -
- 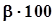 - процентная квантиль плотности распределения “хи - квадрат”.
- процентная квантиль плотности распределения “хи - квадрат”. 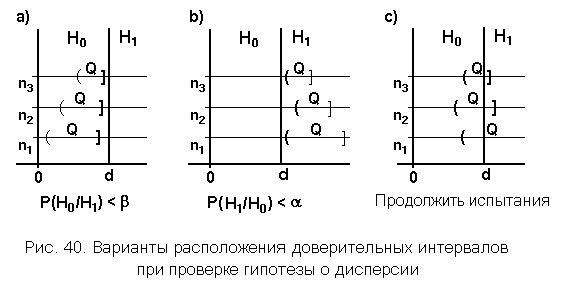
Таким образом, решение о принятии гипотезы  принимается, когда верхняя граница доверительного интервала для дисперсии оказывается меньше заданного значения d, то есть, когда
принимается, когда верхняя граница доверительного интервала для дисперсии оказывается меньше заданного значения d, то есть, когда 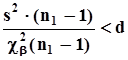 ,В данной ситуации вероятность того, что истинное значение дисперсии находится в зоне, соответствующей гипотезе
,В данной ситуации вероятность того, что истинное значение дисперсии находится в зоне, соответствующей гипотезе 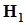 , не превышает b, поскольку в данной ситуации
, не превышает b, поскольку в данной ситуации 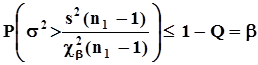 ,значит, в силу монотонности вероятностной меры
,значит, в силу монотонности вероятностной меры 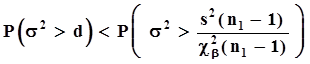 .Из этого следует, что вероятность ошибки второго рода
.Из этого следует, что вероятность ошибки второго рода 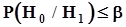 .В соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе
.В соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе 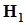 , безразлично. В связи с этим здесь строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода :
, безразлично. В связи с этим здесь строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода : 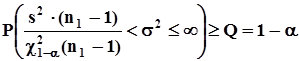 где
где 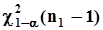 -
- 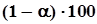 - процентная квантиль плотности распределения “хи - квадрат”. Решение об отклонении нулевой гипотезы принимается, когда нижняя граница доверительного интервала для дисперсии превышает заданное значение d, то есть, когда
- процентная квантиль плотности распределения “хи - квадрат”. Решение об отклонении нулевой гипотезы принимается, когда нижняя граница доверительного интервала для дисперсии превышает заданное значение d, то есть, когда 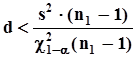 .Вероятность ошибки в этом решении не превышает заданного значения a, поскольку в данной ситуации
.Вероятность ошибки в этом решении не превышает заданного значения a, поскольку в данной ситуации
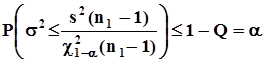 , значит, в силу монотонности вероятностной меры
, значит, в силу монотонности вероятностной меры 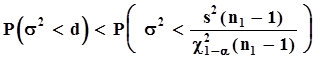 .Из этого следует, что вероятность ошибки первого рода
.Из этого следует, что вероятность ошибки первого рода 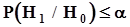 .В третьем варианте, показанном на рис. 40 с), не имеется достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается. После увеличения объема выборки до
.В третьем варианте, показанном на рис. 40 с), не имеется достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается. После увеличения объема выборки до 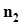 снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения d. Все описанные выше рассуждения и действия повторяются. В конечном итоге описанная последовательная процедура проверки сложной гипотезы о дисперсии должна завершиться выходом доверительного интервала целиком в одну из зон и принятием соответствующей гипотезы.
снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения d. Все описанные выше рассуждения и действия повторяются. В конечном итоге описанная последовательная процедура проверки сложной гипотезы о дисперсии должна завершиться выходом доверительного интервала целиком в одну из зон и принятием соответствующей гипотезы.
50. Проверка сложной гипотезы об интерквантильном промежутке с контролем вероятности ошибок первого и второго рода, приведение проверки этой гипотезы к проверке гипотезы о вероятности, понятие о последовательном анализе А.Вальда.
Плотность распределения генеральной совокупности X - нормальна, дисперсия 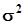 неизвестна. Из генеральной совокупности извлечена выборка
неизвестна. Из генеральной совокупности извлечена выборка 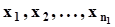 объема
объема 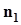 . Проверяется сложная гипотеза
. Проверяется сложная гипотеза  :
: 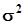 £d против альтернативы
£d против альтернативы 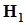 :
: 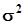 >d.
>d.
Заданы вероятности ошибок первого и второго рода a и b.Естественной статистикой для проверки гипотезы о дисперсии является ее несмещенная оценка: 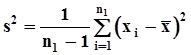 .Доверительный интервал для дисперсии определен в п. 2.4.5 следующим образом:
.Доверительный интервал для дисперсии определен в п. 2.4.5 следующим образом: 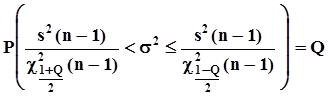 .На рис. 40 показаны варианты расположения доверительного интервала для дисперсии относительно зон, соответствующих гипотезам
.На рис. 40 показаны варианты расположения доверительного интервала для дисперсии относительно зон, соответствующих гипотезам  и
и 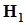 . В соответствии с формулировкой гипотезы и в связи с тем, что
. В соответствии с формулировкой гипотезы и в связи с тем, что 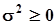 , положение нижней границы доверительного интервала в зоне, соответствующей гипотезе
, положение нижней границы доверительного интервала в зоне, соответствующей гипотезе  , безразлично. По указанным причинам для этого варианта строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью b ошибки второго рода :
, безразлично. По указанным причинам для этого варианта строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью b ошибки второго рода : 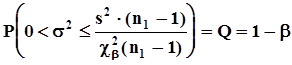 где
где 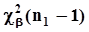 -
- 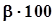 - процентная квантиль плотности распределения “хи- квадрат”.
- процентная квантиль плотности распределения “хи- квадрат”. 
Таким образом, решение о принятии гипотезы  принимается, когда верхняя граница доверительного интервала для дисперсии оказывается меньше заданного значения d, то есть, когда
принимается, когда верхняя граница доверительного интервала для дисперсии оказывается меньше заданного значения d, то есть, когда 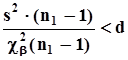 ,В данной ситуации вероятность того, что истинное значение дисперсии находится в зоне, соответствующей гипотезе
,В данной ситуации вероятность того, что истинное значение дисперсии находится в зоне, соответствующей гипотезе 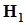 , не превышает b, поскольку в данной ситуации
, не превышает b, поскольку в данной ситуации 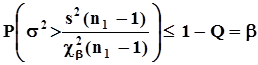 , значит, в силу монотонности вероятностной меры
, значит, в силу монотонности вероятностной меры 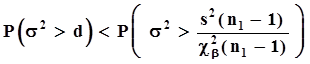 .Из этого следует, что вероятность ошибки второго рода
.Из этого следует, что вероятность ошибки второго рода 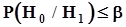 .В соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе
.В соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе 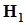 , безразлично. В связи с этим здесь строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода :
, безразлично. В связи с этим здесь строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода : 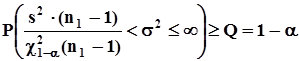 где
где 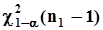 -
- 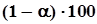 - процентная квантиль плотности распределения “хи - квадрат”. Решение об отклонении нулевой гипотезы принимается, когда нижняя граница доверительного интервала для дисперсии превышает заданное значение d, то есть, когда
- процентная квантиль плотности распределения “хи - квадрат”. Решение об отклонении нулевой гипотезы принимается, когда нижняя граница доверительного интервала для дисперсии превышает заданное значение d, то есть, когда 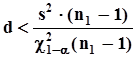 .Вероятность ошибки в этом решении не превышает заданного значения a, поскольку в данной ситуации
.Вероятность ошибки в этом решении не превышает заданного значения a, поскольку в данной ситуации 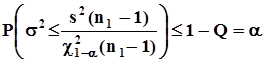 , значит, в силу монотонности вероятностной меры
, значит, в силу монотонности вероятностной меры 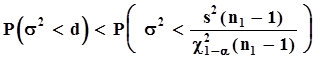 .Из этого следует, что вероятность ошибки первого рода
.Из этого следует, что вероятность ошибки первого рода 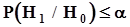 .В третьем варианте, показанном на рис. 40 с), не имеется достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается. После увеличения объема выборки до
.В третьем варианте, показанном на рис. 40 с), не имеется достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается. После увеличения объема выборки до 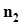 снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения d. Все описанные выше рассуждения и действия повторяются.
снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения d. Все описанные выше рассуждения и действия повторяются.
