Примеры. 66. Проверить, что поле =(y+z) + (z+x) +(x+y) является потенциальным, и найти его потенциал
66. Проверить, что поле 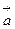 =(y+z)
=(y+z) 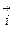 + (z+x)
+ (z+x) 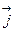 +(x+y)
+(x+y) 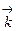 является потенциальным, и найти его потенциал.
является потенциальным, и найти его потенциал.
Решение. Поле 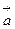 определено во всем пространстве, т.е. в односвязной области, поэтому достаточно проверить, что rot
определено во всем пространстве, т.е. в односвязной области, поэтому достаточно проверить, что rot 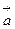 =0. Имеем:
=0. Имеем:
rot 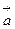 =
=  =(1–1)
=(1–1) 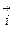 +(1–1)
+(1–1) 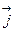 +(1–1)
+(1–1) 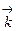 =
= 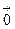 ,
,
что и доказывает потенциальный характер поля 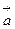 .
.
Найдем потенциал двумя способами.
1 способ.
Для нахождения потенциала воспользуемся формулой (*), беря в качестве М0 начало координат:

2 способ.
Будем снова считать М0(0,0,0).
Пусть  =x
=x 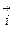 +y
+y 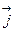 +z
+z 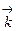 – радиус-вектор точки М(x,y,z), а точка N пробегает отрезок M0М; ее радиус‑вектор
– радиус-вектор точки М(x,y,z), а точка N пробегает отрезок M0М; ее радиус‑вектор  . Точка N имеет координаты tx, ty, tz.
. Точка N имеет координаты tx, ty, tz.
Отсюда d  =
=  dt. Положим
dt. Положим  .
.
Для рассматриваемого поля 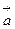 (t)=t(y+z)
(t)=t(y+z) 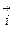 + t(z+x)
+ t(z+x) 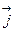 +t(x+y)
+t(x+y) 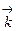 .
.
( 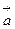 (t),
(t),  )=t(y+z)x+t(z+x)y+t(x+y)z=2t(xy+yz+zx).
)=t(y+z)x+t(z+x)y+t(x+y)z=2t(xy+yz+zx).
Следовательно,  =(xy+yz+zx)
=(xy+yz+zx)  = xy+yz+zx.
= xy+yz+zx.
Ответ: xy+yz+zx.
67. Доказать, что циркуляция потенциального поля по любому замкнутому контуру равна нулю.
Решение: Пусть 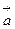 - потенциальное поле и (L) - замкнутый контур, началом и концом которого является точка М(М=М0).
- потенциальное поле и (L) - замкнутый контур, началом и концом которого является точка М(М=М0).
Тогда  , что и требовалось доказать.
, что и требовалось доказать.
