Растровые преобразования прямой (СКЭН преобразования)

Экран (дисплей) – 2D плоскость, для описания которой используется прямоугольная (Декартова) система координат. Единицы измерения по горизонтали и вертикали – реальные. Координаты: экранные и пиксельные.

Экранные координаты определяются вещественными числами x и y (0<= x <= x_max; 0<= y <= y_max).

Пиксельные координаты X и Y (0 <= X <= X_max; 0 <= Y <= Y_max).

Коэффициент масштабирования – отношние пиксельных координат к экранным.

Экранные координаты используются на «нижнем» уровне графики, пиксельные на «верхнем».

Растрирование- это преобразование полутоновых и штриховых изображений в микроштриховые с помощью растра с использованием аппаратных и программных средств.

Н (начало)

К (конец)

(10,20)

(5,10)

Рассмотрим команду построения линии в AutoCad:

Command: line

from point 5,10

to point 10,20

СКЭН – преобразование –растровое преобразование отрезка прямой.

Цель scan-преобразования - представить начальную и конечную координату отрезка в совокупность пикселей в видеобуфере.

Подходы к решению задачи:

1) Использование классического уравнения прямой.

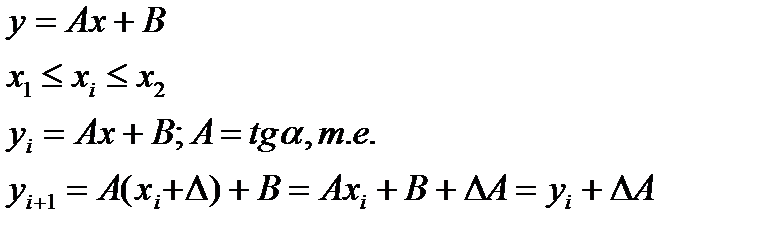
т.е. перебираем все множество точек. Чем меньше зерно (пиксель), тем дольше идет операция. Занимает много времени, а, следовательно, уменьшается быстродействие. Такой подход редко используется, несмотря на простоту.

2) Метод вычисления по приращению (алгоритм Брезенхема)

По известным координатам x и y начального пикселя прямой с помощью прибавления приращений по осям x и y с учётом наклона прямой можно найти положение следующего пикселя. С помощью этого алгоритма формируется набор пикселей, наиболее близко прилежащих к данной прямой.

Допущения:

1. Наша прямая проходит через начало координат;

2. Она проходит под углом α ≤ 45° (0 ≤ tgα ≤ 1);

3. ;

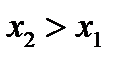4. (0, 0) – координаты начального пикселя.

Тогда уравнение прямой:

α tgα

0<α<45 0<tgα<1

-45<α<0 -1<tgα<0

45<α<90 tgα>1

-90<α<-45 tgα<-1

Начало алгоритма

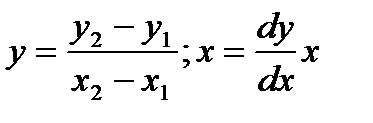
То есть в общем случае мы имеем алгоритм следующего вида: