Непараметрические показатели связи. Ранговые коэффициенты связи

В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам, например рангам, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Данные коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения.

Ранжирование – это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.

Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называются связными.

Пример: Проранжировать предприятия автомобильной промышленности одного из регионов по величине балансовой прибыли:

№ предприятия	Балансовая прибыль, млн. руб.	Ранжирование (ранги)
		6,5
		6,5

Наиболее предпочтительному предприятию, величина балансовой прибыли которого наибольшая, присваивается ранг «1»; затем в порядке уменьшения величины балансовой прибыли были проранжированы все рассматриваемые предприятия автомобильной промышленности.

Принцип нумерации значении исследуемых признаков является основой непараметрических методов изучения взаимосвязи между социально-экономическими явлениями и процессами.

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла . Эти коэффициенты могут быть использованы для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле (для случая, когда нет связных рангов):

где – квадрат разности рангов, 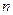– число наблюдений.

Если совокупность значений по исследуемому признаку содержит связные ранги, то коэффициент корреляции Спирмена вычисляется по другой формуле, однако эти вычисления очень громоздки, поэтому на практике используют формулу расчета коэффициента Спирмена (17) как для случая отсутствия, так и наличия связных рангов.

Ранговый коэффициент корреляции Кендалла может также использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты, ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле:

где 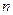– число наблюдений;

– сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Расчет данного коэффициента выполняется в следующей последовательности:

1) значения 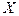ранжируются в порядке возрастания или убывания;

2) значения 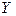располагаются в порядке, соответствующем значениям ;

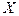3) для каждого ранга 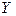определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяется величина как мера соответствия последовательностей рангов по 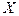и 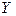и учитывается со знаком (+);

4) для каждого ранга 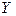определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через и фиксируется со знаком (–);

5) определяется сумма баллов по всем членам ряда: .

Пример:

№п/п	Объем продукции, млн. руб.	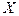Балансовая прибыль, тыс. руб.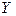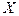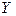
	1,8		1,3
	2,3		1,8
	8,6		2,3
	1,3		3,5
	3,5		3,7
	3,8		3,8
	4,5		4,5
	5,8		5,8
	3,7		6,5
	6,5		8,6

; ; .

Таким образом, , что свидетельствует о наличии близкой к умеренной связи между рассматриваемыми признаками.

Связь между признаками можно признать статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации ) , который вычисляется по формуле:

,

где – количество факторов; 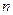– число наблюдений; – отклонение суммы квадратов рангов от средней квадратов рангов.

Пример. Определить тесноту связи между уставным капиталом, числом выставленных акций и числом занятых на предприятиях, выставивших акции на чековые аукционы в 1998 г.

Расчет коэффициента конкордации (данные условные):

№ п/п	Уставный капитал, тыс. руб.	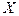Число выставленных акций	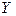Число занятых на п/п				Сумма строк	Квадраты сумм

; – связь слабая.

В случае наличия связных рангов коэффициент конкордации определяется по формуле:

,

где ;

– количество связных рангов по отдельным показателям. Коэффициент конкордации принимает любые значения в интервале [-1; 1].