Дискретное преобразование Лапласа

Дискретное преобразование Лапласа найдем по аналогии с дискретным преобразованием Фурье, заменив в нем 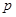на

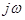
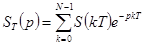. (4.16)

Это позволяет получить спектр по Лапласу, или изображение сигнала. Существует также обратное преобразование Лапласа

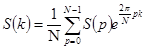. (4.17)

4.5. 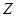– преобразование

Неудобство преобразования является наличие множителя 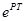или 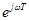, что существенно затрудняет анализ. Его можно упростить при переходе к новой переменной 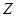связанной с 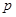следующим соотношением

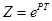, (4.18)

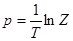. (4.19)

Таким образом приходим к 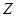– преобразованию

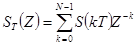. (4.20)

Выражение (4.20) является прямым 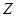– преобразованием. Существует и обратное 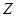– преобразование.

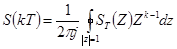(4.21)

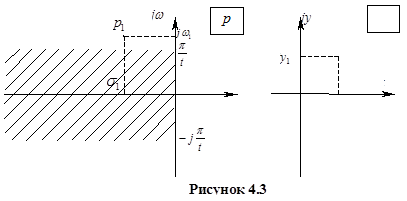
При – преобразовании точка 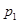комплексной плоскости переходит в точку 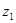комплексной плоскости 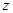(рисунок 4.3).

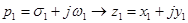. (4.22)

Используя равенство (4.22), запишем

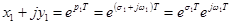, (4.23)

и тогда

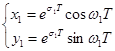. (4.24)

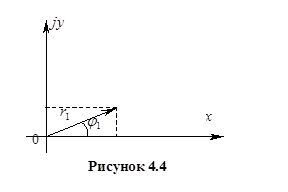
При отражении точки преобразования в полярных координатах (рисунок 4.4) можно записать следующее

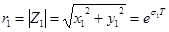, (4.25)

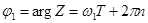, (4.26)

где 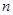– целое число.

Точка 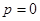плоскости комплексной переменной 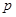переходит в точку, для которой .

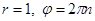И вообще рассматривая ось 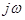плоскости комплексной переменной 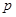, находим, что 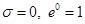, т.е. 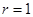. Таким образом, при перемещении по оси 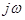плоскости комплексной переменной 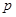, точка отражаемая в плоскости комплексной переменной 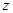будет описывать окружность единичным радиусом с периодом .

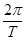Заштрихованная область (рисунок 4.3) отражается во внутренность круга единичного радиуса в плоскости комплексной переменной 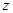. При отражении точек левой полуплоскости плоскости комплексной переменной 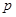, лежащих вне области от 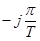до 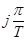(вне заштрихованной области), они снова попадают внутрь круга в плоскости комплексной переменной 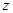. Т.е. вся левой полуплоскость плоскости комплексной переменной 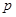отображается во внутренность круга единичного радиуса плоскости комплексной переменной 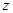, но за пределами заштрихованной области отображение будет происходить с периодическим попаданием в одни и те же точки плоскости комплексной переменной 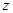. Правая же полуплоскость плоскости комплексной переменной 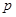отображается во внешнюю часть круга единичного радиуса плоскости комплексной переменной .

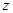Цифровая фильтрация сигналов

Технические возможности современной аппаратуры позволяют проводит обработку сигнала в цифровом коде, где они меньше подвержены влиянию внешних воздействий. Они более стабильны. В частности решается задача фильтрации.

Фильтрация сигнала с точки зрения спектральных представлений сигнала представляет собой изменение спектра сигнала.

С точки зрения временного представления фильтрация – это изменение формы сигнала.