Теоретический материал. Непрерывная случайная величина принимает сплошь все значения из некоторого промежутка, конечного или бесконечного
Непрерывная случайная величина принимает сплошь все значения из некоторого промежутка, конечного или бесконечного. Закон распределения задается либо интегральной функцией распределения F(x), либо дифференциальной функцией 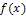 .
.
Эти функции связаны между собой:
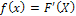
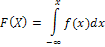
Вероятностный смысл F(x) - это вероятность того, что случайная величина X будет принимать значения меньше, чем х: 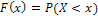 , например
, например 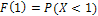 .
.
Вероятностный смысл f(x) - плотность распределения вероятности случайной величины X.
Свойства функции 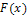 :
:
а) непрерывная, неубывающая функция;
б) 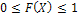 ;
;
Свойства функции 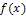 :
:
а) 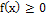 ;
;
б) 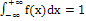 .
.
Вероятность попадания непрерывной случайной величины X в заданный промежуток 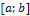 можно найти по формулам:
можно найти по формулам:
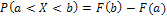
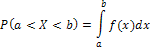
Основные числовые характеристики непрерывной случайной величины:
1. Математическое ожидание: 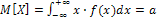 .
.
2. Дисперсия: 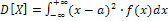 .
.
Второй способ вычисления дисперсии:
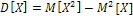 , где
, где
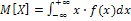 ;
; 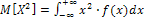
3. Среднее квадратическое отклонение: 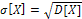 .
.
Начальный теоретический момент порядка к непрерывной случайной величины X определяется равенством 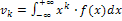 .
.
Центральный теоретический момент порядка к непрерывной случайной величины X определяется равенством 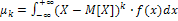 . В частности, если все возможные значения X принадлежат интервалу, то
. В частности, если все возможные значения X принадлежат интервалу, то 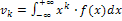 ,
, 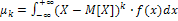 . Очевидно, что если
. Очевидно, что если 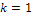 , то
, то 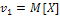 ,
, 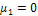 ; если
; если 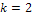 , то
, то 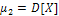 .
.
Центральные моменты выражаются через начальные моменты по формулам:
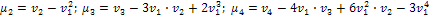 .
.
