Эмпирическая функция распределения. Каждая генеральная совокупность имеет функцию распределения F(x), которая обычно неизвестна

Каждая генеральная совокупность имеет функцию распределения F(x), которая обычно неизвестна. По выборке можно найти эмпирическую функцию распределения 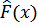, где на основании закона больших чисел Бернулли вместо вероятностей берутся относительные частоты (частости)

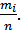Процесс нахождения эмпирической функции распределения 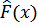аналогичен процессу нахождения функции распределения 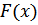по формуле

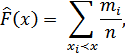(1)

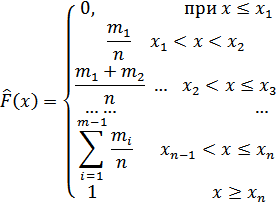
В качестве представителя интервала берется его середина или правый конец интервала. Объединяя точки, ординатами которых являются накопленные частости, получаем ломаную линию, являющуюся довольно хорошим приближением графика функции распределения непрерывной случайной величины.

Эмпирическая функция 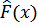обладает всеми свойствами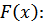

1. Значение эмпирической функции принадлежит отрезку [0,1],

;

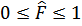2. 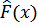– неубывающая функция;

3. если 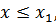то 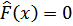, если x_k – наибольший вариант, то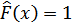

при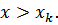

Для построения графика 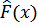откладываем значения функции в интервале от 0 до 1 (рис. 1).

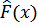
X

(рис. 1)

Вычисление числовых характеристик

Построив вариационный ряд и изобразив его графически, мы получим первоначальное представление о закономерностях, имеющих место при испытаниях. Для дальнейшего изучения значений случайной величины используют числовые характеристики вариационных рядов, которые называются статистическими характеристиками или оценками. С этой целью выделяют некоторые постоянные, которые представляют вариационный ряд в целом и отображают присущие для совокупности закономерности. Это среднее арифметическое, выборочная дисперсия, среднеквадратичное отклонение, мода, медиана, эксцесс, коэффициент асимметрии.

Среднее арифметическое определяется по формулам:

(2)

где n – число испытаний,

x_i– результаты испытаний.

Чаще пользуются формулой, где получают средневзвешенное арифметическое:

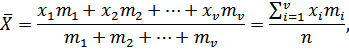(3)

где x_i– среднее значение i – го интервала; m_i­ – соответствующая интервальная частота; v – число интервалов.

Выборочная дисперсия

Выборочной дисперсией случайной величины х называется среднее арифметическое квадратов отклонений наблюдаемых значений этой величины от их среднего арифметического

Для вариационного ряда вычисляют средневзвешенную выборочную дисперсию:

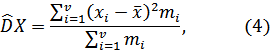
где m_i – интервальная частота;x_i– среднее значение для i – интервала;

V – количество интервалов.

Выборочная дисперсия обладает одним существенным недостатком: если среднее арифметическое выражается в тех же единицах, что и значение случайной величины, то дисперсия в квадратных единицах. Этого недостатка можно избежать, взяв в качестве меры рассеивания выборочное средне квадратичное отклонение.

Определение.Выборочным среднеквадратичным отклонением называется арифметический квадратичный корень из выборочной дисперсии и обозначается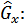

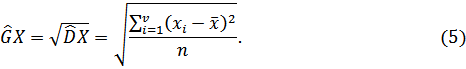
Мода выборки.Модой выборки является значение, имеющее максимальную частоту. Если вариационный ряд представлен интервалом, то мода вычисляется по формуле:

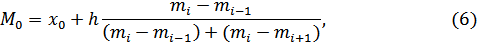
где x₀– начало модального интервала, имеющего максимальную частоту;h – длина интервала; m_i – частота модального интервала; m_i-1,m_i+1 – частоты соответственно предшествующего и последующего интервалов.

Медиана. Определение.Медианой выборки называется значение серединного элемента вариационного ряда. Если вариационный ряд интервальный, то значение медианы вычисляется по приближенной формуле

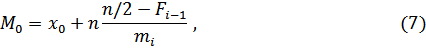
где x₀ – начало медианного интервала, т.е. интервала, который содержит серединный элемент; h– длина интервала; F_i-1 – сумма частот интервалов, предшествующих медианному; m_i– частота медианного интервала; 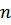– объем выборки.

Коэффициент асимметрии. Определение.Выборочным коэффициентом асимметрии называется число, определяемое формулой:

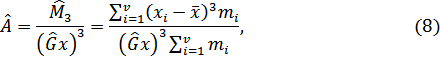
где 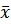– среднее–арифметическое, 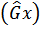– выборочное среднеквадратичное отклонение; 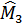- центральный выборочный момент 3-го порядка; 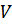– число интервалов.

Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон ассиметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.

В случае отрицательного коэффициента асимметрии пологий «спуск» полигона должен быть слева, в противном случае – справа. В первом случае асимметрия называется левосторонней, а во втором – правосторонней.

Выборочный эксцесс. Определение.Выборочным эксцессом или коэффициентом крутости называется число E, определяемое формулой:

где 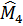– выборочный момент 4-го порядка;

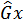_­– выборочное средне квадратичное отклонение.

Выборочный эксцесс служит для сравнения на «крутость» выборочного закона распределения с нормальным распределением. В случае нормального распределенияЕ=0.

В случае положительного эксцесса полигон более крутой по сравнению с нормальным распределением. Если выборочному распределению соответствует отрицательный эксцесс, то соответствующий полигон имеет более пологую вершину по сравнению с нормальным распределением.

Центральный выборочный момент. Определение.Центральным выборочным моментом к-го порядка называется среднее арифметическое к-х степеней отклонений наблюдаемых значений случайной величины от 4-х среднеарифметического и обозначается :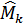

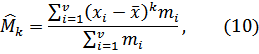
где 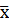– среднеарифметическое;

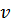– количество интервалов;

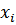– среднее значение i–го интервала;

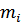– частота i–го интервала.

Для расчета числовых характеристик рекомендуется предварительно рассчитать таблицу 2.