Влияние качки на точность гирокомпаса

Подобно всякому одногироскопному компасу, нестабилизированному относительно его главной оси, рассматриваемый прибор подвержен влиянию качки. У него также возникает четвертная девиация, хотя механизм ее образования несколько иной, чем у обычного компаса.

Физическую природу возникновения четвертной девиации легко уяснить из рис. 3.2. Хотя гиросфера гирокомпаса и уравновешена, она образует вместе со следящей сферой маятниковую систему.

При качке эта система совершает колебания относительно точки подвеса. Нас интересует составляющая этих колебаний в плоскости Е — W. Учитывая весьма малый период собственных колебаний, можно считать, что эта маятниковая система следит за положением кажущейся вертикали, т. е. непрерывно устанавливается под углом

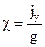
к истинной вертикали. Напомним, что на регулярной бортовой качке 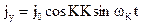. На тот же угол поворачиваются оси прецессии. Одновременно меридиональные силы инерции воздействуют на индикатор горизонта. Если бы постоянная времени индикатора горизонта была равна нулю, снимаемый с него сигнал в точности соответствовал бы приложенному ускорению.

Поскольку на качке оси двигателей стабилизации рассогласуются с осями соответствующих торсионов вследствие колебаний чувствительного элемента в плоскости Е—W, это привело бы к появлению постоянной составляющей момента горизонтальной стабилизации относительно оси прецессии OZ.

В результате получается полная аналогия с обычным одногироскопным гирокомпасом, у которого постоянный вертикальный момент создает четвертную девиацию на качке.

В действительности у индикатора горизонта имеется существенная постоянная времени. Благодаря этому чувствительный элемент индикатора горизонта не успевает следить за меридиональным ускорением. Возникающие за счет небольших перемещений моменты малы и не приводят к образованию заметных девиаций.

Чтобы убедиться в этом, определим величину постоянной составляющей момента 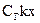по оси OZ гирокомпаса.

Очевидно, 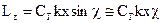, причем 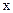определяется из уравнения

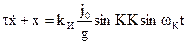(3.12)

Найдем частное решение последнего уравнения в виде

.

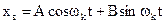Подставляю правую часть полученного равенства в (3.12) и сравнивая члены с одинаковыми гармониками, получим:

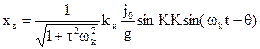
где

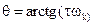
Таким образом, момент 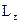равен

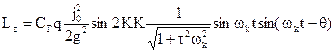
Постоянная часть момента 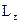, очевидно, будет

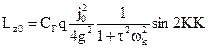
Приравнивая момент 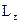направляющему моменту, получим следующее выражение четвертной погрешности рассматриваемого гирокомпаса:

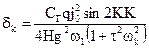
Как видно, величина четвертной девиации существенно зависит от постоянной времени индикатора горизонта.

Например, при 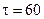сек множитель 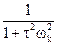для возможных периодов качки лежит в пределах 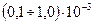. Вследствие столь малых величин указанного множителя четвертная девиация ГК с КУ пренебрежимо мала.

Особенность рассматриваемого гирокомпаса заключается еще и в том, что карданов подвес ЧЭ не позволяет снимать отсчет курса в плоскости горизонта.

Величина соответствующей этому кардановой ошибки определяется известной формулой

,

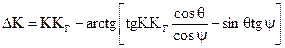где 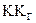- компасный курс в горизонтальной плоскости;

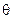- угол крена;

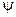- угол дифферента.

Из этой формулы видно, что карданная ошибка достигает максимума на четвертных курсах. При регулярной бортовой качке с амплитудой 10° величина карданной ошибки не превышает .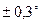

Вопросы для самоконтроля

1. В чем заключается отличие гирокомпасов с НУ от ГК с КУ?

2. Какой элемент ГК с КУ является основным источником информации, позволяющий превратить свободный гироскоп в гирокомпас?

3. Виды погрешностей присуще ГК с КУ?