Математические схемы описания технических систем

1.3.1. Непрерывно–детерминированные модели ( D – схемы)

Математические схемы такого вида отражают динамику процессов, протекающих во времени в системе. Поэтому они называются D– схемы. Частным случаем динамических систем являются системы автоматического управления.

Линейная автоматическая система описывается линейным дифференциальным уравнением вида

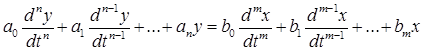(1.1)

где x(t)- задающее воздействие или входная переменная системы; y(t) - состояние системы или выходная переменная; 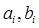- коэффициенты; t - время.

На рис.1 представлена укрупненная функциональная схема системы автоматического управления, где 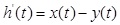– сигнал ошибки; 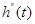- управляющее воздействие; f(t) - возмущающее воздействие. Данная система основана на принципе отрицательной обратной связи, так как для приведения выходной переменной y(t) к ее заданному значению используется информация об отклонении между ними. По ней можно разработать структурную схему и математическую модель в виде передаточной функции или в виде дифференциального уравнения (1.1), в котором для простоты предполагается, что точки приложения возмущающих воздействий совпадают с входом системы.

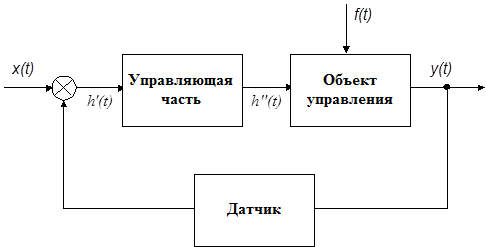
Рис.1.1. Структура системы автоматического управления

Непрерывно- детерминированные схемы (D- схемы) выполняются на аналоговых вычислительных машинах (АВМ).

1.3.2. Дискретно–детерминированные модели ( F – схемы )

Основным видом дискретно–детерминированных моделей является конечный автомат.

Конечным автоматом называют дискретный преобразователь информации, способный под воздействием входных сигналов переходить из одного состояния в другое и формировать сигналы на выходе. Это автомат с памятью. Для организации памяти в описание автомата вводят автоматное время и понятие состояние автомата.

Понятие «состояние» автоматаозначает, что выходной сигнал автомата зависит не только от входных сигналов в данный момент времени, но и учитывает входные сигналы, поступающие ранее. Это позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.

Всякий переход автомата из одного состояния в другое возможен не ранее, чем через дискретный интервал времени. Причем сам переход считается, происходит мгновенно, то есть не учитывают переходные процессы в реальных схемах.

Существует два способа введения автоматного времени по которому автоматы делятся на синхронные и асинхронные.

В синхронных автоматах моменты времени, в которых фиксируются изменения состояний автомата, задаются специальным устройством – генератором синхросигналов. Причем сигналы поступают через равные интервалы времени – 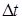. Частота тактового генератора выбирается такой, чтобы любой элемент автомата успел закончить свою работу до появления очередного импульса.

В асинхронном автомате моменты перехода автомата из одного состояния в другое заранее не определены и зависят от конкретных событий. В таких автоматах интервал дискретности является переменным.

Также существуют детерминированные и вероятностные автоматы.

В детерминированных автоматах поведение и структура автомата в каждый момент времени однозначно определены текущей входной информацией и состоянием автомата.

В вероятностных автоматах они зависят от случайного выбора.

Абстрактно конечный автомат можно представить как математическую схему (F – схему), которая характеризуется шестью видами переменных и функций:

1) конечное множество x(t) входных сигналов (входной алфавит);

2) конечное множество y(t) выходных сигналов (выходной алфавит);

3) конечное множество z(t) внутренних состояний (алфавит состояний);

4) начальное состояние автомата z₀ , ;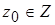

5) функция переходов 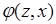автомата из одного состояния в другое;

6) функция выходов 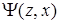автомата.

Абстрактный конечный автоматимеет один вход и один выход. В каждый дискретный момент времени t=0,1,2,... F– автомат находится в определенном состоянии z(t) из множества Z – состояний автомата, причем в начальный момент времени t=0 он всегда находится в начальном состоянии z(0)=z₀ . В момент t , будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал 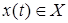и выдать на выходном канале сигнал 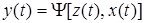, переходя в состояние

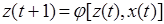, где .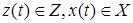

Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y , то есть , если на вход конечного автомата , установленного в начальное состояние z₀ , подавать в некоторой последовательности буквы входного алфавита 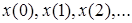, которые составляют входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита 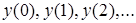образуя выходное слово.

Следовательно, работа конечного автомата происходит по следующей схеме: на каждом t – ом такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который автомат реагирует переходом на (t+1)– ом такте в новое состояние z(t+1) и выдачей некоторого выходного сигнала.

В зависимости от способа определения выходного сигнала синхронные абстрактные конечные автоматы подразделяются на два типа:

- F – автомат первого рода, также называется автомат Мили:

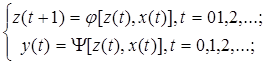
- F – автомат второго рода:

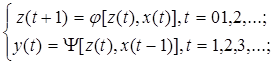
Автомат второго рода, для которого

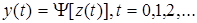
называется автомат Мура – функция выходов не зависит от входной переменной x(t).

Чтобы задать конечный F – автомат, необходимо описать все элементы множества .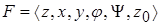

Существует несколько способов задания работы F – автоматов среди которых наибольшее применение нашли табличный, графический и матричный.

1.3.3. Дискретно – непрерывные модели

Процессы в линейных импульсных и цифровых системах автоматического управления описываются дискретно – разностными уравнениями вида:

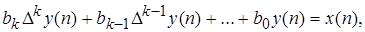(1.2)

где x(n) –решетчатая функция входного сигнала; y(n) –решетчатая функция выходного сигнала, которая определяется решением уравнения (1.2); b_k – постоянные коэффициенты; 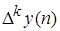– разность к – го порядка; t=nT, где nT – n–ый момент времени, T – период дискретности ( в выражении (1.2) он условно принят за единицу).

Уравнение (1.2) можно представить в другом виде:

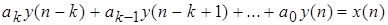(1.3)

Уравнение (1.3) представляет собой рекуррентное соотношение, которое позволяет вычислить любой (i+1) –й член последовательности по значениям предыдущих её членов i,i-1,... и значению x(i+1).

Основным математическим аппаратом моделирования цифровых автоматических систем является Z– преобразование, которое базируется на дискретном преобразовании Лапласа. Для этого необходимо найти импульсную передаточную функцию системы, задаться входной переменной и, варьируя параметрами системы, можно найти лучший вариант проектируемой системы.

1.3.4. Дискретно – стохастические модели ( Р - схемы)

К дискретно – стохастической модели относится вероятностный автомат. В общем, виде вероятностный автомат является дискретным потактным преобразователем информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически. Поведение автомата зависит от случайного выбора.

Применение схем вероятностных автоматов имеет важное значение для проектирования дискретных систем, в которых проявляется статистически закономерное случайное поведение.

Для Р – автомата вводится аналогичное математическое понятие, как и для F – автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (x_i ,z_s ), где x_i и z_s элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функци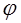и и 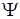, что с их помощью осуществляется отображение 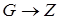и 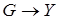, то говорят, что 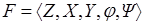определяет автомат детерминированного типа.

Функция переходов вероятностного автомата определяет не одно конкретное состояние, а распределение вероятностей на множестве состояний

(автомат со случайными переходами). Функция выходов также есть распределение вероятностей на множестве выходных сигналов (автомат со случайными выходами).

Для описания вероятностного автомата введем в рассмотрение более общую математическую схему. Пусть Ф – множество всевозможных пар вида (z_k ,y_j), где y_j – элемент выходного подмножества Y. Далее потребуем чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

элементы из Ф ...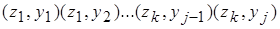

... ...

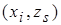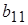
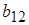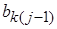
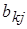
где 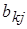– вероятности перехода автомата в состояние z_k и появления на выходе сигнала y_j , если он был в состоянии z_s и на его вход в этот момент времени поступал сигнал x_i.

Число таких распределений , представленных в виде таблиц равно числу элементов множества G. Если обозначить это множество таблиц через В, то тогда четверку элементов 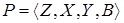называют вероятностным автоматом ( Р – автоматом). При этом .

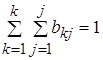Частным случаем Р– автомата, задаваемого как 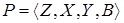являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано(Z– детерминированный вероятностный автомат, Y–- детерминированный вероятностный автомат соответственно).

Очевидно, что с точки зрения математического аппарата задание Y – детерминированного Р – автомата эквивалентно заданию некоторой марковской цепи с конечным множеством состояний. В связи с этим аппарат марковских цепей является основным при использовании Р– схем для аналитических расчетов. Подобные Р– автоматы используют генераторы марковских последовательностей при построении процессов функционирования систем или воздействий внешней среды.

Марковские последовательности, согласно теореме Маркова, –это последовательность случайных величин, для которой справедливо выражение

,

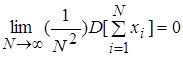где N – количество независимых испытаний; D–- дисперсия.

Такие Р– автоматы (Р– схемы) могут быть использованы для оценки различных характеристик исследуемых систем как для аналитических моделей, так и для имитационных моделей с использованием методов статистического моделирования.

Y – детерминированный Р– автомат можно задать двумя таблицами: переходов (табл.1.1) и выходов (табл.1.2).

Таблица 1.1

zk			zk
	z1	z2	...	zk-1	zk
z1	P11	P12	...	P1(k-1)	P1k
z2	P21	P22	...	P2(k-1)	P2k
...	...	...	...	...	...
zk	Pk1	Pk2	...	Pk(k-1)	Pkk

Таблица 1.2

Z...	z1	z2	...	zk-1	zk
Y...	yi1	yi2	...	yi(k-1)	yik

Где P_ij – вероятность перехода Р– автомата из состояния z_i в состояние z_j, при этом .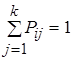

Таблицу 1.1 можно представить в виде квадратной матрицы размерности 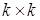. Такую таблицу будем называть матрицей переходных вероятностей или просто матрицей переходов Р- автомата, которую можно представить в компактной форме:

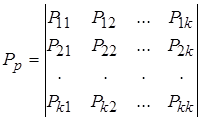
Для описания Y– детерминированного Р–автомата необходимо задать начальное распределение вероятностей вида:

Z...	z1	z2	...	zk-1	zk
D...	d1	d2	...	dk-1	dk

где d_k– вероятность того, что в начале работы Р– автомат находится в состоянии z_k, при этом .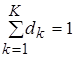

И так, до начала работы Р– автомат находится в состоянии z₀ и в начальный (нулевой) такт времени меняет состояние в соответствии с распределением D. После этого смена состояний автомата определяется матрицей переходов Р. С учетом z₀ размерность матрицы Р_р следует увеличить до 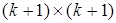, при этом первая строка матрицы будет (d₀,d₁,d₂,...,d_k), а первый столбец будет нулевым.

Пример.Y– детерминированный Р– автомат задан таблицей переходов:

Таблица 1.3

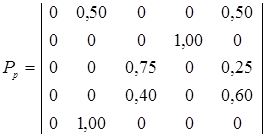
и таблицей выходов

Таблица 1.4

Z	z0	z1	z2	z3	z4
Y

С учетом таблицы 1.3 граф переходов вероятностного автомата представлен на рис.1.2.

Требуется оценить суммарные финальные вероятности пребывания этого автомата в состоянии z₂ и z₃, т.е. когда на выходе автомата появляются единицы.

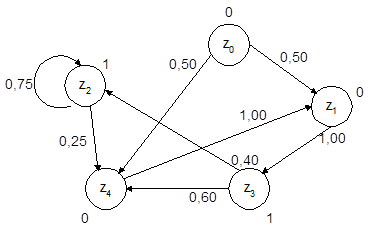
Рис. 1.2. Граф переходов

При аналитическом подходе можно использовать известные соотношения из теории марковских цепей и получить систему уравнений для определения финальных вероятностей. Причем начальное состояние можно не учитывать в виду того, что начальное распределение не оказывает влияние на значения финальных вероятностей. Тогда таблица 1.3 примет вид:

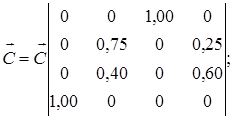
где 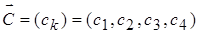– финальная вероятность пребывания Y– детерминированного Р– автомата в состоянии z_k.

В результате получаем систему уравнений:

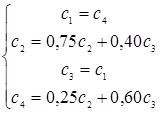(1.4)

К данной системе следует добавить условие нормировки:

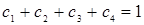(1.5)

Теперь решая систему уравнений (1.4) совместно с (1.5), получаем:

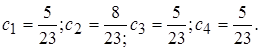
Таким образом, при бесконечной работе заданного автомата на его выходе будет формироваться двоичная последовательность с вероятностью появления единицы, равной: .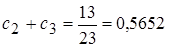

Кроме аналитических моделей в виде Р– схем можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.

1.3.5. Непрерывно–стохастические модели (Q– схемы)

Такие модели рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания, которые называют Q– схемами. Такие Q– схемы применяются при формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

К процессам обслуживания можно отнести: потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов сети ЭВМ . Характерным признаком для функционирования таких систем или сетей является случайное появление заявок на обслуживание. Причем в любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания и , собственно, сам процесс обслуживания заявки. Представим это в виде некоторого i-го прибора обслуживания П_i (рис.1.3), состоящего из накопителя заявок Н_i , в котором может находится одновременно 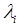заявок; К_i – канал обслуживания заявок.

На каждый элемент прибора П_i поступают потоки событий, в накопитель Н_i поток заявок 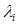, на канал К_i – поток обслуживания И_i.

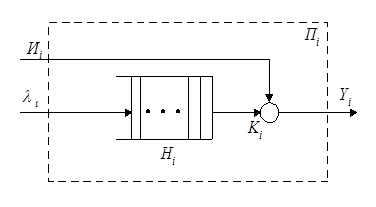
Рис.1.3. Прибор обслуживания

Потоки событий могут быть однородными, если он характеризуется только последовательностью поступления этих событий ( 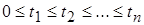), или неоднородными, если он характеризуется набором признаков события, например таким набором признаков : источник заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т.п.

Обычно при моделировании различных систем применительно к каналу К_i можно считать, что поток заявок 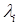на входе К_i образует подмножество неуправляемых переменных, а поток обслуживания И_i – образует подмножество управляемых переменных.

Те заявки, которые по различным причинам не обслуживаются каналом К_i, образуют выходной поток У_i.