Реляционная алгебра. Полнота ограниченного множества операторов
Недостатки модели
Основной недостаток – невозможность реализации отношения «многие ко многим» в рамках одной базы данных. Реализация такого отношения на основе двух БД затрудняет управление.
9. Сетевая модель данных. Достоинства и недостатки.
Сетевая (графовая) модель основана на рекомендациях рабочей группы по базам данных КОДАСИЛ (CODASYL).
Согласно рекомендациям, база данных делится на области, те – на записи, состоящие из полей. С другой стороны, база состоит из наборов, а те – из записей. Набор включает владельца и подчинённых участников набора, объединяющихся в линейный список.
Запись– иерархия, образованная из простейших (атомарных) элементов данных, их групп и повторяющихся групп.
Тип набора – множество допустимых экземпляров набора записи. К набору относятся записи – участники набораи владелец набора. Записи-владельцы (участники) могут быть одновременно владельцами (участниками) других наборов.
Доступ к участнику набора производится только через владельца. Тип набора имеет имя (уникальность владельца). Универсальный владелец в сетевой модели – это СУБД. Через нее выполняется доступ к самым «верхним» владельцам. Допускается и набор без владельца – сингулярный набор. В этом случае доступ к информации производит система, играя роль универсального владельца.
Ограничения КОДАСИЛ
1. Тип набора определяет отношение 1:М между типом записи-владельца и типом записи-участника.
2. Экземпляр типа записи-участника может участвовать только в одном экземпляре типа набора.
В сетевой модели отношение записей представляет собой граф, не имеющий циклов. Иерархическая модель может быть представлена как частный случай сетевой.
В сетевой базе данных запрещено дублирование данных. Принадлежность записи к различным наборам реализуется ссылками.
Наборы в сетевой базе данных могут иметь управляющие атрибуты. Атрибут «обязательный-необязательный» определяет поведение СУБД при удалении владельца экземпляра набора. В первом случае члены набора удаляются при удалении владельца, во втором случае – нет. Атрибут «автоматический-ручной» определяет способ включения в набор. В первом случае члены набора включаются в нужный экземпляр набора автоматически, во втором случае в нужный набор запись включается по команде из прикладной программы.
В сетевой базе данных, как и иерархической, существует понятие текущего состояния. В него входят сведения о текущем состоянии структуры базы, структуры наборов, связи и т.п. Наличие этих данных позволяет эффективно осуществлять доступ к данным, контролировать их целостность. Недостаток такого централизованного представления – трудности с изменением структуры данных.
Достоинства
Ÿ реализуется отношение «многие ко многим»;
Ÿ высокая производительность.
Недостатки
Ÿ Трудность изменения структуры базы данных;
Ÿ Накопление «информационного мусора» за счет некорректных удалений и сбоев;
Ÿ слабая выразительность языка запросов.
Первая СУБД, построенная по сетевой модели – IDMS (1971 г.). Правами на нее обладает компания Computer Associates, она до сих пор поставляет и развивает эту СУБД. Примером может служить и СУБД IMAGE/1000 фирмы Hewlett-Packard.
10.Реляционная модель данных. Основные принципы. Компоненты модели. Достоинства и недостатки модели.
Принципы
Реляционная модель - альтернатива сетевой модели, предложенная Коддом. В основу модели Кодд положил три базовых принципа (стремления):
1) независимость данных на логическом и физическом уровнях – стремление к независимости;
2) создание структурно простой модели – стремление к коммуникабельности;
3) использование концепции языков высокого уровня для описания операций над порциями информации – стремление к обработке множеств.
В качестве структурной единицы выбрано отношение n-го порядка. Отношение n-го порядка – математическое множество, в котором порядок строк не имеет значения. Модель
Напомним, что модель данных – это структура и комбинация трех составляющих:
1) типов структур данных;
2) операторов или правил вывода;
3) общих правил целостности.
Структурную часть реляционной модели составляют следующие компоненты:
Ÿ отношения неопределенного порядка - таблица;
Ÿ атрибуты(столбец) – атомарные данные, характеризующие отношения;
Ÿ домены – множества допустимых значений атрибутов;
Ÿ кортежи(строки) – совокупности значений всех атрибутов отношения, взятых по одному для каждого атрибута, представленные строками таблицы;
Ÿ возможные ключи – множество атрибутов, однозначно определяющее кортеж;
Ÿ первичные ключи – для каждого отношения это один из возможных ключей.
Только нормализованное отношение может быть объектом реляционной модели. Определение.Отношения нормализованы, если каждый его атрибут атомарен, то есть, не заменим другим отношением.
Определение.В отношении существует одна или более групп атрибутов, однозначно идентифицирующих кортеж. Это возможные ключи. Один из них объявляется первичным. Атрибуты, входящие в первичный ключ, называются первичными.
Таким образом, мы сформулировали следующие свойства отношений:
1) Нормализованные отношения представляются в виде табличной структуры.
2) Упорядоченность кортежей теоретически несущественна.
3) Все кортежи различны.
Определение.Реляционная БД – совокупность изменяющихся во времени нормализованных отношений, которые могут быть связаны через общие домены.
Достоинство реляционной модели – простота определения данных и их изменения.
Недостаток – проблемы с организацией связи.
11. Операции, реализующие изменение отношений во времени.
Размещение дополнительной информации производится операцией добавления ADD(r; A1=d1, A2=d2 , ..., An=dn). (Вариант для фиксированного порядка атрибутов: ADD(r; d1, d2, ..., dn))
Возможные ошибки при добавлении:
1) добавляемый кортеж не соответствует схеме;
2) некоторые значения не принадлежат требуемым доменам;
3) после добавления появляется совпадение по ключу.
В любом случае операция не выполняется.
Удаление информации производится операцией DEL(r; A1=d1, ..., An=dn) или DEL(r; d1, ..., dn).
Если K={B1, B2 , ..., Bm } – ключ отношения, для удаления достаточно записать DEL(r; B1=b1, B2=b2 , ..., Bm=bm).
Возможная ошибка – отсутствие удаляемого кортежа. Заметим, что допускается удаление последнего кортежа, то есть, пустое отношение может существовать.
Модификация информации производится операцией изменения. Пусть {C1, ... Cp} {A1, ... An}. Тогда операция модификации записывается следующим образом: CH(r; A1=d1, ..., An=dn ; C1=c1,..., Cn=cp) или, в случае ключа, CH(r; B1=b1, ..., Bm=bm ; C1=c1, ..., Cn=cp).
Того же эффекта можно достигнуть последовательным удалением изменяемого кортежа и добавлением нового. Поэтому ошибки модификации представляют собой объединение ошибок удаления и добавления.
12.Операции реляционной алгебры: булевы операции. Активное дополнение.
Операции, рассмотренные в предыдущей лекции – это операции не над отношениями, а над отдельными кортежами. Далее мы рассмотрим операции над отношениями. Это, во-первых, обычные булевы операции, а во-вторых, группа специальных операторов.
Булевы операции
К булевым операциям относятся операции пересечения, объединения, разности. Пусть r, s – отношения со схемой R. Они могут рассматриваться как подмножества множества всех кортежей, определяемых этой схемой, поэтому к ним применимы булевские операции.
Пересечением называется отношение q(R) = r(R)∩s(R), содержащее кортежи, которые одновременно принадлежат и r, и s. Объединением называется отношение q(R) = r(R)Us(R), содержащее кортежи, которые принадлежат либо r, либо s. Разностью называется отношение q(R) = r(R) - s(R), содержащее кортежи, которые принадлежат r, но не принадлежат s. Или формально:
r∩s ={t |(t r)&(t s)};
rUs ={t |(t r) (t s)};
r–s ={t |(t r)&(t s)}.
Заметим, что r∩s = r – (r – s), то есть достаточно лишь двух операций.
Обозначим dom(R) множество всех кортежей над атрибутами из схемы R и их доменами: dom(R) = {t(d1 d2 … dn)| di dom(Ai)}. Дополнение отношения определим как r(R): r = dom(R) - r(R). Но если какой-либо атрибут из R имеет бесконечный домен, r будет тоже иметь бесконечное число кортежей, то есть по определению не будет отношением.
Определение.Пусть r(A1, A2,..., An) – отношение, Di = dom(Ai). Тогда активный домен атрибута Ai относительно r – это множество adom(Ai,r) = {d Di | t r, t(Ai)=d}.
Пусть adom(R,r) – множество всех кортежей над атрибутами из R и их активными доменами относительно r: adom(R, r) = {t(d1 d2 … dn)| di adom(Ai, r)}. Тогда активным дополнением r будем называть (r’=adomR,r’-r)?. Так как число значений атрибутов, принадлежащих кортежам из r, конечно, то активное дополнение всегда будет отношением.
13. Операции реляционной алгебры: выбор; свойства выбора.
Пусть теперь A – это некоторый атрибут отношения r(R) и a dom(A) – элемент множества значений, которые может принимать отображение t на этом атрибуте. Выберем из отношения r те кортежи, для которых отображение t(A)=a, то есть, на A принимает значение a, и результат обозначим через ϬA = a(r). Это унарная операция (применяется к одному отношению), результат которой – новое отношение r (R).
Определение. Выбором ϬA = a(r) называется отношение r (R) = ϬA = a(r) {t r | t(A)=a}.
Пусть r и s – отношения со схемой R; A, B, C,… – конечное число атрибутов в R, пусть a dom(A), b dom(B), c dom(C),… . Тогда верны следующие утверждения.
Утверждение 6.1.Операторы выбора коммутативны относительно операции композиции (т.е. результат их применения не зависит от последовательности):
ϬA =а°ϬB = b(r) ϬA = a(ϬB = b(r)) = ϬB = b(ϬA = a(r))≡ϬB = b°ϬA = a(r).
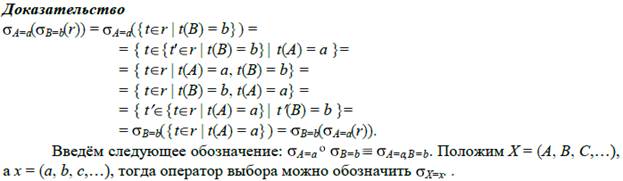
Утверждение 6.2.Операция выбора дистрибутивна относительно бинарных булевых операций:
ϬA = a(r s) = ϬA = a(r) γϬA = a(s), где γ - принадлежит{∩,U , – }.
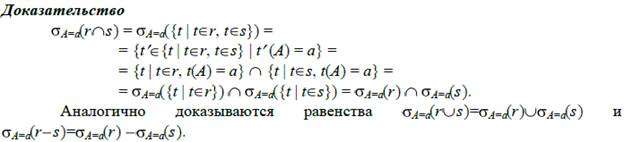
Замечание.Операции выбора и активного дополнения не перестановочны (не комму- тируют).
14. Операции реляционной алгебры: проекция; свойства проекции.
Пусть r – отношение со схемой R, X - подмножество R.
Определение.Проекцией πX(r) называется отношение r (X) = πX(r)≡{t(X) | t r }.
Это унарная операция, но в отличие от операции выбора, которая выдаёт строки по заданным условиям, она выдаёт столбцы, заголовки которых перечислены в X.
Утверждение 6.3.Операторы проекции и выбора перестановочны относительно композиции:
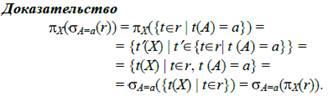 πX °ϬA = a (r)≡ πX(ϬA = a (r)) = ϬA = a (πX(r)) ϬA = a° πX (r).
πX °ϬA = a (r)≡ πX(ϬA = a (r)) = ϬA = a (πX(r)) ϬA = a° πX (r).
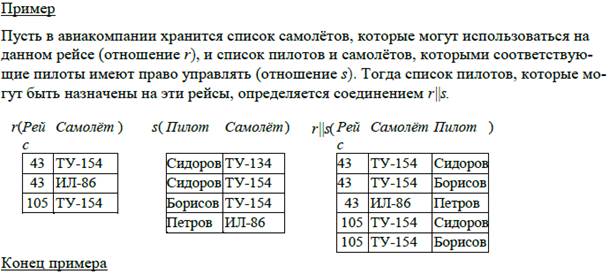
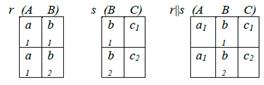
15. Операции реляционной алгебры: соединение. Пример соединения.

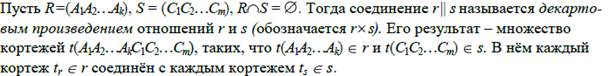

16. Операции реляционной алгебры: свойства соединения.
Свойства соединения
Свойство 1.Имитация выбора.
С помощью оператора соединения найдём 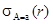 для отношения r(R). Для этого определим отношение s(A) с одним единственным кортежем t таким, что t(A) = a. Тогда r || s =
для отношения r(R). Для этого определим отношение s(A) с одним единственным кортежем t таким, что t(A) = a. Тогда r || s = 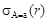
Доказательство
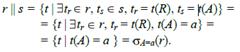
Свойство 2. Обобщённая операция выбора.
Введём новое отношение s(A) с k кортежами t1, t2,…, tk, где ti(A) = ai и ai  dom(A), i =1, 2,…, k.
dom(A), i =1, 2,…, k.
Тогда r || s = 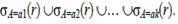
Свойство 3.Коммутативность оператора соединения.
Из определения следует, что r || s = s || r.
Свойство 4.Ассоциативность оператора соединения.
Для отношений q, r, s (q || r) || s = q || (r || s). Следовательно, последовательность соединений можно записывать без скобок.
Свойство 5.Многократные соединения.
Пусть r1(S1), r2(S2),…, rn(Sn) – отношения, R = S1 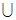 S2
S2 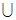 …
… 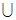 Sn. Обозначим S – последовательность схем S1, S2,…, Sn. Пусть t1, t2,…, tn – последовательность кортежей, ti
Sn. Обозначим S – последовательность схем S1, S2,…, Sn. Пусть t1, t2,…, tn – последовательность кортежей, ti  ri, i = 1, 2,…, n.
ri, i = 1, 2,…, n.
Определение.Кортежи t1, t2,…, tn соединимы на S, если существует кортеж t на R, что ti = t(Si) для каждого i = 1, 2,…, n. Кортеж t называется результатом соединения кортежей t1, t2,…, tn на S.
Если в определении принять n=2 и если кортежи t1 и t2 соединимы на S=S1, S2 с результатом t, то t1=t(S1), t2=t(S2), следовательно, t  r(S1) || r(S2). Обратно, если t
r(S1) || r(S2). Обратно, если t  r(S1)||r(S2), то должны существовать t1 и t2 в r(S) такие, что t1=t(S1), t2=t(S2), то есть они соединимы на S с результатом t. Следовательно, r(S1) ||r(S2) состоит из результатов соединений соединимых на S кортежей t1 и t2 .
r(S1)||r(S2), то должны существовать t1 и t2 в r(S) такие, что t1=t(S1), t2=t(S2), то есть они соединимы на S с результатом t. Следовательно, r(S1) ||r(S2) состоит из результатов соединений соединимых на S кортежей t1 и t2 .
Лемма.Отношение r1 || r2 ||…|| rn состоит из всех кортежей t, которые являются результатом соединения соединимых на S кортежей ti ri, i = 1, 2,…, n.
Не каждый кортеж каждого отношения может войти в соединение.
Определение.Отношения r1, r2,…, rn полностью соединимы, если каждый кортеж в каждом отношении является членом списка соединимых на S кортежей.
Свойство 6.Проекция соединения.
Свойство показывает связь проекции и соединения. Похоже, что они взаимнообратны, но это не так.
Пусть r(R) и s(S) – отношения, q = r || s, RS – схема q. Пусть r’ = 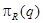 ), тогда r’
), тогда r’ 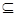 r (для любого кортежа t из отношения q верно t(R)
r (для любого кортежа t из отношения q верно t(R)  r, а r’ ={t(R)| t
r, а r’ ={t(R)| t  q}).
q}).
Включение может быть собственным:

Может быть равенство (r = r’):
Ясно, что равенство получается при соединении полностью соединимых отношений, но может быть и без этого.
Если s’ = 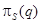 , то r’ = r и s’ = s тогда и только тогда, когда r и s – состоят из полностью соединимых кортежей, то есть полностью соединимы.
, то r’ = r и s’ = s тогда и только тогда, когда r и s – состоят из полностью соединимых кортежей, то есть полностью соединимы.
Свойство 7.Соединение проекций.
Поменяем местами проекции и соединения. Пусть q – отношение со схемой RS, r = 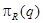 , s =
, s = 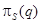 . Пусть q′ = r || s. Если t
. Пусть q′ = r || s. Если t  q, то t(R
q, то t(R  ) r, t(S)
) r, t(S)  s
s 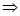 t
t  q′, т.е. q′
q′, т.е. q′ 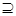 q. При q′ = q отношение разложимо без потерь на схемы R и S.
q. При q′ = q отношение разложимо без потерь на схемы R и S.
Свойство 8.Соотношение операций объединения и соединения.
Пусть r и r – отношения со схемой R и s – отношение со схемой S. Покажем, что (rr) || s = (r || s)(r || s).
Обозначим левую часть равенства как q 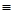 (r
(r 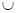 r’)||s, а правую – q’
r’)||s, а правую – q’ 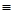 (r || s)
(r || s) 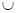 (r’ || s). Для кортежа t
(r’ || s). Для кортежа t  q найдутся кортежи
q найдутся кортежи 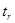 и
и 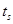 такие, что t =
такие, что t = 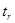 ||
|| 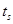 , причем
, причем 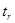
 r или
r или 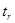
 r’ и
r’ и 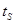
 s’. Если
s’. Если 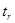
 r, то t
r, то t  r || s, если же
r || s, если же 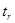
 r’, то t
r’, то t  r’ || s, то есть q
r’ || s, то есть q 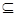 q’. Чтобы установить включение q
q’. Чтобы установить включение q 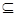 q’, выберем t
q’, выберем t  q’. Тогда t
q’. Тогда t  r || s или t
r || s или t  r’ || s, следовательно, t
r’ || s, следовательно, t  (r
(r 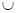 r’) || s. Из q
r’) || s. Из q 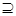 q’ и q
q’ и q 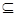 q’ следует q = q.
q’ следует q = q.
17. Операции реляционной алгебры: деление.
Определение.Пусть r(R) и s(S) – отношения, S 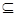 R. Положим R = R - S. Тогда r, разделенное на s – это отношение r’(R’)=
R. Положим R = R - S. Тогда r, разделенное на s – это отношение r’(R’)= 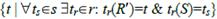
Отношение r’– частное от деления r на s, что обозначается r’= r 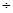 s. Иначе r
s. Иначе r 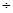 s – это максимальное подмножество r’ множества
s – это максимальное подмножество r’ множества 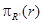 , такое, что r’ || s
, такое, что r’ || s  r. Соединение здесь – декартово произведение.
r. Соединение здесь – декартово произведение.
18. Построение отношений. Переименование атрибутов. Пример. Одновременное переименование.
Постоянные отношения.
При обсуждении соединения мы показали, что результат операции выбора может быть получен при выполнении операции соединения с постоянным отношением. Введём специальный способ записи постоянных отношений.
Определение.Пусть A1,…,An – различные атрибуты, а c_i является константой из dom(Ai) для 1 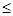 i
i 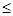 n, тогда< с1 :А1,…,сn :An> – постоянный кортеж <с1,…,сn> над схемой А1А2…Аn.
n, тогда< с1 :А1,…,сn :An> – постоянный кортеж <с1,…,сn> над схемой А1А2…Аn.
Постоянное отношение над схемой А1А2…Аn представляется как множество кортежей. Пусть c_ij – константа из dom(Ai ) для 1 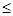 i
i 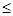 n и 1
n и 1 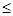 j
j 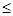 k, тогда
k, тогда
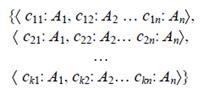
представляет отношение, которое обычно записывалось бы так:

В случае, когда отношение состоит из одного кортежа, фигурные скобки иногда опускаются. Для кортежа с единственным атрибутом опускаются угловые скобки.
Утверждение.Постоянное отношение с любым числом кортежей k и любым числом атрибутов n может быть построено из постоянных отношений с одним кортежем и одним атрибутом с помощью операторов соединения и объединения.
Переименование атрибутов
Пример
Отношение использование определяет назначение конкретного самолета с заданным бортовым номером на рейс в определенную дату.
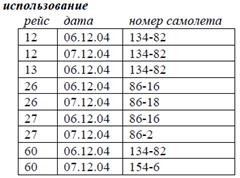
Требуется узнать все пары рейсов, которые используют один и тот же самолет в один и тот же день. Для этого хорошо было бы соединить отношение использование с его копией, игнорируя связи по столбцу рейс. Но для этого нужно, чтобы атрибут рейс в копии назывался по-другому, например, рейс2. Переименование атрибутов производится соответствующим оператором.
Определение.Пусть r – отношение со схемой R, A  R, В
R, В 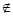 R – A, dom(A)=dom(B). Пусть R’ = (R – A)B. Тогда r с A, переименованным в В (обозначается
R – A, dom(A)=dom(B). Пусть R’ = (R – A)B. Тогда r с A, переименованным в В (обозначается 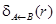 ) есть отношение r’(R’ ) =
) есть отношение r’(R’ ) = 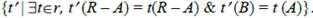
Пример (продолжение)
Отношение с искомыми парами рейсов:

Конец примера
Пусть r – отношение со схемой R,
A1,…, Ak  R;
R;
B1,…, Bk 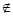 R – (A1…Ak); (1)
R – (A1…Ak); (1)
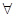 i: dom(Bi) = dom(Ai).
i: dom(Bi) = dom(Ai).
Обозначим одновременное переименование атрибутов A1,…, Ak в B1,…, Bk как 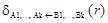 Благодаря условию (1) оно всегда может быть записано в виде последовательности переименований. Если это условие не выполняется, без введения дополнительных атрибутов такую замену выполнить нельзя. Очевидный пример – обмен
Благодаря условию (1) оно всегда может быть записано в виде последовательности переименований. Если это условие не выполняется, без введения дополнительных атрибутов такую замену выполнить нельзя. Очевидный пример – обмен 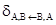
19. Операции реляционной алгебры: Эквисоединение, естественное и – соединение.
Мы увидели, что отношения можно соединять по одноимённым атрибутам. Чтобы соединить отношения по различным атрибутам с одинаковыми доменами, требуется выполнить две операции: переименование и соединение. Подобные соединения с переименованиями встречаются очень часто, поэтому эту пару операций разумно представить одной.
Определение.Пусть r(R), s(S) – отношения, Ai  R , Bi
R , Bi  S , dom(Ai) = dom(Bi), 1
S , dom(Ai) = dom(Bi), 1 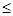 i
i 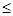 m, Ai ≠ Bi. Эквисоединением r и s по A1, A2,…,Am и B1, B2,…, Bm называется отношение
m, Ai ≠ Bi. Эквисоединением r и s по A1, A2,…,Am и B1, B2,…, Bm называется отношение
q(RS) = 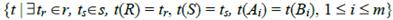
Эту операцию будем обозначать следующим образом:
r [A1 = B1, A2 = B2,…, Am = Bm] s.
Заметим, что для однозначного определения операции эквисоединения достаточно условия Ai ≠ Bi для всех атрибутов, входящих в сравнение. Однако обычно требуют, чтобы в эквисоединении все атрибуты различались по именам, то есть, чтобы R 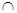 S = пустому множеству . Это не сильное ограничение, так как путем переименования атрибутов в s и r можно добиться пустого пересечения их схем.
S = пустому множеству . Это не сильное ограничение, так как путем переименования атрибутов в s и r можно добиться пустого пересечения их схем.
Замечание.Если в эквисоединении нет сравнений, то оно совпадает с декартовым произведением: r [ ] s = r s.
Соединение, определённое ранее, будем называть естественным.
Утверждение.Эквисоединение может быть выражено через переименование и естественное соединение.
Естественное соединение также может быть выражено через эквисоединение. Например, для отношений r(A, B, C), s(B, C, D), атрибутов B’ и C’ с dom(B’) = dom(B), dom(C’) = dom(C):
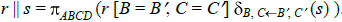
До сих пор при сравнении значений доменов мы пользовались лишь равенством, но их можно сравнивать, используя и неравенства. В общем случае вводится 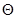 – множество символов бинарных операций над парами доменов.
– множество символов бинарных операций над парами доменов.
Определение.Если знак сравнения 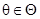 , а A и B – атрибуты, то говорят, что A
, а A и B – атрибуты, то говорят, что A 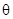 -сравним с B, если
-сравним с B, если 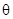 – бинарное отношение в dom(A)
– бинарное отношение в dom(A) 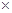 dom(B).
dom(B).
Определение.Атрибут A 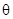 -сравним, если он
-сравним, если он 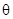 -сравним сам с собой.
-сравним сам с собой.
Расширим оператор выбора, используя понятие 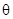 -сравнимости. Пусть r – отно-шение со схемой R, атрибут A
-сравнимости. Пусть r – отно-шение со схемой R, атрибут A  R, a
R, a  dom(A) – константа,
dom(A) – константа, 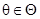 , A
, A 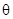 -сравним. Тогда расширенный оператор выбора
-сравним. Тогда расширенный оператор выбора 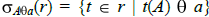 . Аналогично этот оператор определяется для случая сравнения между атрибутами, с учетом того, что B
. Аналогично этот оператор определяется для случая сравнения между атрибутами, с учетом того, что B  R, dom(B)=dom(A):
R, dom(B)=dom(A):
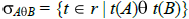 .
.
Эквисоединение – это расширенное соединение для сравнения разных столбцов на равенство. Можно не ограничиваться равенством, а воспользоваться любой операцией 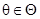 .
.
Определение.Пусть r(R) и s(S) – отношения, для которых R 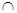 S = пустое , и пусть A
S = пустое , и пусть A  R и B
R и B  S
S 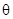 -сравнимы для . Тогда
-сравнимы для . Тогда 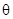 -соединением называется отношение q(RS) = {t |
-соединением называется отношение q(RS) = {t | 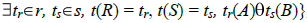 , которое обозначается q(RS) = r [A
, которое обозначается q(RS) = r [A 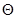 B] s.
B] s.
20. Реляционная алгебра Кодда. Алгебра А (алгебра Дэйта). Полнота Алгебры А.
Реляционная алгебра. Полнота ограниченного множества операторов
Обозначим U – множество атрибутов (универсум), D – множество доменов, dom – полная функция из U в D, R = {R1, R2,…, Rp} – множество схем, Ri 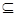 U, d = {r1(R1), r2(R2),…, rp(Rp)} – множество наборов отношений,
U, d = {r1(R1), r2(R2),…, rp(Rp)} – множество наборов отношений, 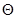 – множество бинарных отношений над доменами из D.
– множество бинарных отношений над доменами из D.
Определение. Реляционная алгебра над U, D, dom, R, d, 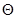 – семиместный кортеж B=( U, D, dom, R, d,
– семиместный кортеж B=( U, D, dom, R, d, 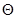 , O), где O– множество операторов объединения, пересечения, разности, активного дополнения, проекции, естественного соединения, деления, переименования, которые используют атрибуты из U,и оператор выбора, использующий операторы из
, O), где O– множество операторов объединения, пересечения, разности, активного дополнения, проекции, естественного соединения, деления, переименования, которые используют атрибуты из U,и оператор выбора, использующий операторы из 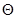 .
.
Теорема. Для выражения E над реляционной алгеброй существует выражение E’ над ней же, которое определяет ту же функцию и использует лишь операторы (1) постоянных отношений с единственным атрибутом и единственным кортежем, (2) выбора с одним сравнением, (3) естественного соединения, (4) проекции, (5) объединения, (6) разности, (7) переименования.
Следствие.Для реляционной алгебры с операцией дополнения в формулировке предыдущей теоремы можно заменить операцию разности (пункт 6) операцией дополнения.
21. Операторы расщепления и фактора. Примеры использования
Следующие два оператора не относятся к реляционной алгебре, так как в результате их применения из одного отношения получаются два, а для операторов реляционной алгебры результат – одно отношение.
Определение.Пусть 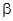 (t) – предикат на кортежах над R, тогда расщеплением r по
(t) – предикат на кортежах над R, тогда расщеплением r по 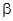 называется пара отношений (s, s’), каждое со схемой R, такие, что s = {t
называется пара отношений (s, s’), каждое со схемой R, такие, что s = {t  r |
r | 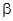 (t)} и s’ = { t
(t)} и s’ = { t  r |
r | 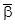 (t)}. Обозначается эта пара SPLIT
(t)}. Обозначается эта пара SPLIT 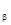 (r).
(r).
Пример
Рассмотрим список студентов
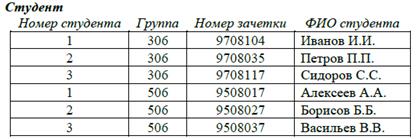
Разобьём его на два по группам. Для этого воспользуемся операцией расщепления с предикатом 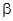 (t) = (t(Группа) = 306). Тогда SPLIT
(t) = (t(Группа) = 306). Тогда SPLIT 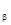 (Студент) = (гр306, гр506):
(Студент) = (гр306, гр506):
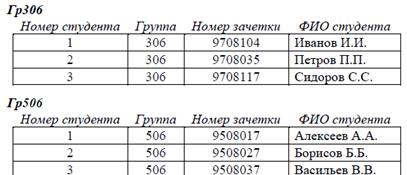
Конец примера
Пример демонстрирует возможности оператора при организации работы с распределёнными данными. Если по какой-то причине невыгодно держать все данные на одном обрабатывающем узле (например, пользователь определённой группы данных территориально удалён), их следует разделить с помощью оператора расщепления. Для совместного использования данные объединяются оператором объединения.
Следующий оператор тоже используется для распределения данных, но другим способом. В этом случае на две части делится схема отношения, а для восстановления исходного отношения без потерь в обе получившиеся схемы добавляется уникальный атрибут-метка, который принимает одинаковое значение на кортежах, образованных из общего.
Определение.Пусть дано отношение r(R) и B1, B2,…, Bk  R, L
R, L 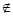 R. Тогда фактором будем называть пару следующих отношений: (s, s’) = FACTOR (r; B1, B2,…, Bk; L), где s = s((R – B1B2…Bk)L), s’ = s’ (B1B2…BkL), причём s и s’ соединяются по L без потерь.
R. Тогда фактором будем называть пару следующих отношений: (s, s’) = FACTOR (r; B1, B2,…, Bk; L), где s = s((R – B1B2…Bk)L), s’ = s’ (B1B2…BkL), причём s и s’ соединяются по L без потерь.
Действие последнего оператора рассмотрим на примере.
Пример
Задан список абитуриентов, сдающих вступительные экзамены. Для обеспечения секретности каждый абитуриент на каждом экзамене получает шифр. Проверяющий видит только шифр и работу, но не фамилию или номер экзаменационного листа абитуриента.
Чтобы исключить доступ ко всей информации, разделим отношение на два, добавив в каждое одинаковую метку: Дело(метка, Группа, Номер экз.листа, ФИО) и Шифр(Шифр, метка). Воспользуемся оператором FACTOR(Абитуриент; шифр; метка) = (Дело, Шифр).
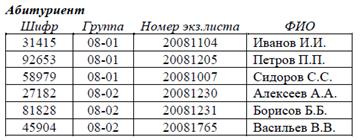
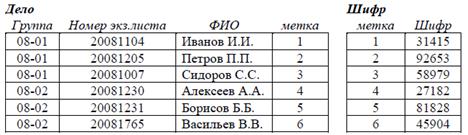
Конец примера
Следующий пример применения оператора фактора не столь очевиден. Мы его используем для получения более компактной базы данных, которая будет, кроме того, более удобной для сопровождения.
Пример
Рассмотрим список отдыхающих в некотором доме отдыха. Во время заезда админист-ратор интересуется у отдыхающих, курят они или храпят. Его цель – для минимизации конфликтов разместить курильщиков с курильщиками, храпящих – с храпящими.
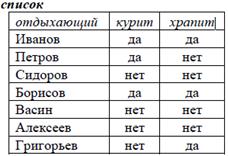
Получившийся список довольно неудобен. Мало того, что он велик, так при попытке учесть ещё какое-нибудь обстоятельство придётся реструктурировать очень большую таблицу. Тогда разделим исходное отношение на два таким образом, чтобы в первом были записаны все комбинации свойств отдыхающих, обозначенные целыми числами (метками), а во втором вместо столбцов со свойствами появился столбец с метками. Набору свойств соответствует метка, взятая из соответствующего кортежа первого отношения. Это достигается применением оператора FACTOR(список; курит, храпит; метка) = (свойства, новый_список).
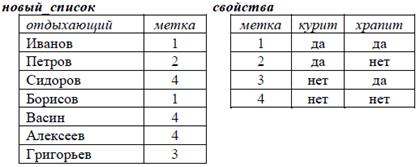
Действительно, по определению оператора фактора получившиеся отношения должны быть соединимы по метке и не более того, что мы и наблюдаем. Но в первом примере одному кортежу первого отношения соответствовал единственный кортеж второго, а здесь нет. Для достижения полученного эффекта мы использовали правило: если атрибуты B1, B2,…, Bk  R из определения оператора не содержат ключ, одинаковые кортежи t(B1B2…Bk) помечаются одинаковыми метками. В противном случае одинаковыми метками помечаются кортежи t(R-B1B2…Bk).
R из определения оператора не содержат ключ, одинаковые кортежи t(B1B2…Bk) помечаются одинаковыми метками. В противном случае одинаковыми метками помечаются кортежи t(R-B1B2…Bk).
22. Функциональная зависимость. Алгоритм проверки существования функциональной зависимости в отношении.
Определение.Пусть R – схема отношения, X,Y 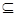 R. Множество атрибутов Y функционально зависит от X тогда и только тогда, когда в любой момент времени для каждого из различных значений Y существует только одно из различных значений X. Другими словами, для любого r(R), ti , tj
R. Множество атрибутов Y функционально зависит от X тогда и только тогда, когда в любой момент времени для каждого из различных значений Y существует только одно из различных значений X. Другими словами, для любого r(R), ti , tj  r, ti(Y) ≠ tj(Y)
r, ti(Y) ≠ tj(Y) 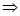 ti(X) ≠ tj(X).
ti(X) ≠ tj(X).
Эквивалентный термин: множество X определяет Y. Обозначение – X  Y. Левую часть функциональной зависимости X называют детерминантом.
Y. Левую часть функциональной зависимости X называют детерминантом.
23. Нормальные формы. 1 нормальная форма. Её связь с постановкой задачи.
Некоторые функциональные зависимости могут быть нежелательны в конкретной схеме, так как они при модификации базы данных приводят к трудностям, называемым аномалиями модификации (аномалиями добавления, изменения и удаления). Для приведения схемы в корректный вид используется замена одного множества отношений другим, сохраняющим ее эквивалентность. Такое преобразование составляет суть процесса нормализации. В результате исходное небольшое число таблиц с «большой» схемой, обладающее непривлекательными свойствами, заменяется большим числом таблиц с «меньшей» схемой, этими свойствами не обладающих. Говорят, что полученные отношения удовлетворяют некоторой нормальной форме.
Нормальные формы, в которых находятся отношения, составляют иерархию, в которой формы с большими номерами не обладают некоторыми нежелательными свойствами, характерными для форм с меньшими номерами. В теории нормальных форм для реляционных БД рассматривается шесть уровней нормализации: 1НФ – 5НФ и форма Бойса-Кодда (промежуточная между 3НФ и 4НФ). Каждый из следующих уровней ограничивает типы допустимых функциональных зависимостей отношения. Функциональные зависимости отношения описывают его семантику. Уровень нормализации зависит от семантики отношения.
Надо заметить, что процесс нормализации не всегда сопровождает проектирование данных. Чаще всего в процессе построения информационной модели проектировщик, руководствуясь естественным порядком построения отношений, строит их сразу в третьей нормальной форме. Нормализация отношений требуется на этапе сопровождения (развития) программной системы, когда выявляются не известные ранее функциональные зависимости, в результате чего отношения теряют нормальную форму.
Нормальная форма (1НФ)
Согласно определению отношения, все его атрибуты атомарны, то есть не могут быть разделены семантически на более мелкие элементы. Отношение, обладающее этим свойством, называется нормализованным или, что то же самое, находящимся в первой нормальной форме (1НФ).
Определение.Отношение находится в 1НФ, если все значения его атрибутов атомарны, то есть, для каждого отношения r(R), если AR, adom(A,r) атомарен .
Пример
Пусть для отношения со схемой рейс (Номер, Пункт назначения, Вылет) атрибут Вы-лет определен как пара (День, Время):
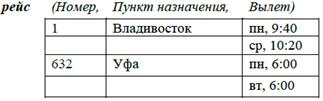
В этом случае легко реализовать запросы типа «Выдать все рейсы до Уфы», в отличие от запроса «Выдать все рейсы, вылетающие утром». С точки зрения второй задачи отношение не находится в 1НФ. Преобразование очевидно: отношение заменяется другим со схемой
рейс (Номер, Пункт назначения, День, Время).
24. Полная функциональная зависимость. 2 нормальная форма.
Нормальная форма (2НФ)
Широко распространённая ошибка при проектировании баз данных – попытка объявить в качестве первичного ключа суперключ: дескать, лишний атрибут в ключе не повредит. Такая практика на деле приводит к значительным неприятностям.
Определение.Функциональная зависимость X=(A1,A2,...,Ak)  B полная, если B зависит от всех Ai из X. Если существует X'
B полная, если B зависит от всех Ai из X. Если существует X'  B, где X' – собственное подмножество X, функциональная зависимость неполная.
B, где X' – собственное подмножество X, функциональная зависимость неполная.
Определение.Отношение находится во 2НФ, если оно находится в 1НФ и каждый непервичный атрибут функционально полно зависит от ключа.
Определение запрещает в качестве ключа использовать суперключ, если отношение находится во 2НФ.
Пример
Задано отношение со схемой поставки (Поставщик, Товар, Цена), для которого опре-делены следующие ограничения:
Ÿ Товар могут поставлять разные поставщики.
Ÿ Цена одинаковых товаров одинакова.
Ÿ Поставщик может поставлять разные товары.
Эти ограничения определяют следующие функциональные зависимости:
Поставщик, Товар Цена
Товар Цена
Здесь налицо неполная функциональная зависимость цены от ключа.
Аномалия включения: новый товар не включается в БД без поставки.
Аномалия удаления: поставки прекращаются – удаляются сведения о товаре.
Аномалия обновления: изменение цены влечет полный пересмотр.
Преобразование:
Поставки (поставщик, товар)
Цена товара (товар, цена)
25. Транзитивная зависимость. 3 нормальная форма.
Нормальная форма (3НФ)
Соответствие отношения 2НФ не гарантирует от других аномалий. Неприятные явле-ния могут обнаружиться, если есть функциональная зависимость атрибута от непер-вичных.
Определение.Атрибут A транзитивно зависит от X, если существует Y такой, что выполняется условие X  Y &
Y & 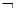 (Y
(Y  X) & Y
X) & Y  A & X
A & X  A, A
A, A 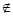 XY.
XY.
Условие (Y X) означает, что Y – множество заведомо не первичных атрибутов.
Определение.Отношение находится в 3НФ, если оно находится в 1НФ и в нем отсут-ствует транзитивная зависимость атрибутов от первичных атрибутов.
Пример
Решается задача, связанная с определением складов для отделений больницы. Задача ставится руководством отделения, для которого важно, чтобы за его отделением был закреплен склад определенного объема, причем только один. Тогда для отношения со схемой хранение (Отделение, Склад, Объем) существует единственная функциональная зависимость:
Отделение  Склад
Склад
Через некоторое время выяснилось, что нужно следить и за состоянием складов безот-носительно их принадлежности к отделению. Это порождает вторую функциональную зависимость:
Склад  Объем
Объем
Таким образом, отношение оказалось не в 3НФ (существует транзитивная зависимость объема от отделения через склад: Отделение  Склад &
Склад & 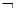 Склад
Склад  Отделение & Склад
Отделение & Склад  Объем & Отделение
Объем & Отделение  Объем).
Объем).
Аномалия включения: нет отделения, получающего товар с этого склада – нет сведе-ний об объеме.
Аномалия удаления: отделение перестает получать товар – нет данных о складе.
Аномалия обновления: изменение объема склада влечет полный пересмотр.
Преобразование:
хранение (Отделение, Склад)
объем склада (Склад, Объем)
26. Многозначная зависимость. 4 нормальная форма.
Нормальная форма (4НФ)
Другая распространённая ошибка при проектировании баз данных, кроме использования суперключа – наличие в одном отношении атрибутов, связанных отношением «один ко многим» или, что ещё хуже – «многие ко многим». Изначально эта связь может быть не очевидна, но по мере уточнения семантики отношения проявляется.
Определение.A многозначно определяет B в R (или B многозначно зависит от A), если каждому значению A соответствует множество (возможно, пустое) значений B, не зависимых от других атрибутов из R. Обозначение: A 
 B.
B.
Пример
Задано отношение преподаватель(Ид-преп, Дети, Курсы, Должность), которое связывает уникальный идентификатор (код) преподавателя с его семейными обстоятельствами (наличием детей) и служебным положением (читаемые курсы). Будем считать, что атрибуты Ид-преп и Дети находятся в отношении 1:M, а Ид-преп и Курсы – в отношении M:N. Здесь наличие детей и читаемые курсы – независимые атрибуты, то есть присутствуют многозначные зависимости Ид-преп 
 Дети и Ид-преп
Дети и Ид-преп 
 Курсы.
Курсы.
Определение.Отношение находится в 4НФ, если оно находится в 1НФ и в нем от-сутствует нефункциональные многозначные зависимости. Другое определение – для любой нетривиальной зависимости X 
 Y множество атрибутов X содержит ключ).
Y множество атрибутов X содержит ключ).
Пример
Зависимость между преподавателем, детьми и курсами из предыдущего примера при-водит к тому, что при появлении нового ребенка приходится добавлять столько корте-жей, сколько курсов читает этот преподаватель, а при добавлении курса следует доба-вить столько кортежей, сколько у преподавателя детей.
Преобразование:
R1(Ид-преп, Дети)
R2(Ид-преп, Курсы)
R3(Ид-преп, Должность)
27. Проектирование данных. Уровни абстракции
Процессы проектирования
В ходе разработки проекта нужно ответить на следующие вопросы:
Ÿ что представляют собой требования заказчиков и в какой форме они выражены;
Ÿ как они преобразуются в структуру базы данных;
Ÿ как часто и каким образом структура базы данных должна перестраиваться.
Рассматриваются три уровня абстракции для определения структуры данных: концептуальный (точка зрения заказчика), логический (точка зрения разработчика) и физический (точка зрения администратора БД).
Концептуальный уровень – наиболее общее представление об информационном содержании предметной области. Представляется в виде концептуальной модели (КМ). КМ обладает высокой степенью стабильности, она проблемно-ориентирована и не зависит от конкретной СУБД, операционной системы и аппаратного обеспечения. Ее поведение должно быть полностью предсказуемо.
Концептуальное представление оперирует основными элементарными данными предметной области, называемыми сущностями. Сущности описываются атрибутами. Данные могут находиться в некотором отношении друг с другом: образовывать ассоциации. Эти ассоциации называются связями. Концептуальная модель должна поддерживать согласованность связей в пределах уровня детализации.
Обычно для концептуального представления используется модель «Сущность-Связь» (ER-модель), введенная Ченом, которая графически выражается ER-диаграммами.
Логический уровень представления оперирует такими понятиями, как запись, компоненты записи, связи между записями. Соответствующая ему модель называется логической (ЛМ), она представляет собой отображение концептуальной модели в среду конкретной СУБД.
Физический уровень демонстрирует физическое хранение данных. На этом уровне используются такие понятия, как физические блоки, файлы, хранимые записи, указатели.
Есть и другая классификация уровней представления данных. Согласно стандарту ANSI / SPAC, архитектура БД представлена трехуровневой моделью с внешним, концептуальным и внутренним уровнями. В отличие от предыдущей модели, это не модель проектирования, а модель оперирования данными.
Внешний уровень – описание на языке пользователя структуры данных, вида и формы их представления, а также описание операций манипулирования данными.
Концептуальный уровень – наиболее общее представление об информационном содержании предметной области. Определение совпадает с приведенным ранее.
Внутренний уровень – организованная совокупность структурированных данных, отображение концептуальной модели в конкретную среду хранения. Объединяет ранее определенные логическую и физическую модели.
28. Концептуальное проектирование. Выявление требований.
