Методика розв’язання оберненої задачі
У даному випадку відомий вектор швидкості течії 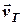 (його величина
(його величина 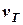 та напрям – курс
та напрям – курс 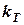 ), а також величина
), а також величина 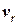 швидкості руху судна відносно води та шляховий кут
швидкості руху судна відносно води та шляховий кут 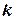 абсолютної швидкості
абсолютної швидкості 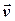 . Отже в рівнянні
. Отже в рівнянні
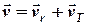
потрібно знайти 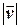 – величину абсолютної швидкості та курс
– величину абсолютної швидкості та курс 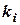 – напрям вектора
– напрям вектора 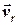 .
.
Графічно – задача зводиться до побудови трикутника векторів за відомими двома кутами 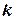 та
та 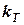 (тобто за одним відомим кутом у трикутнику швидкостей) і двома сторонами
(тобто за одним відомим кутом у трикутнику швидкостей) і двома сторонами 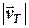 та
та 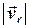 .
.
З початкової точки 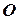 проводимо промінь по заданому шляховому куту
проводимо промінь по заданому шляховому куту 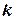 – визначаємо траєкторію абсолютного руху судна. З точки
– визначаємо траєкторію абсолютного руху судна. З точки 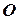 відкладаємо вектор швидкості течії
відкладаємо вектор швидкості течії 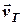 – визначаємо точку
– визначаємо точку 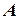 – місце, куди течія знесе судно у відсутності відносного руху (роботи двигуна).
– місце, куди течія знесе судно у відсутності відносного руху (роботи двигуна).
Далі умовно відключаємо течію і визначаємо, куди може потрапити судно з точки 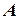 за рахунок роботи двигуна так отримуємо точку
за рахунок роботи двигуна так отримуємо точку 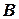 на траєкторії абсолютного руху судна. Напрям
на траєкторії абсолютного руху судна. Напрям 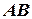 визначає істинний курс
визначає істинний курс 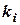 , а довжина
, а довжина 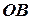 модуль абсолютної швидкості.
модуль абсолютної швидкості.
Аналітично – у трикутнику швидкостей 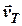 ,
, 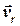 та
та 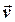 відомі дві сторони,
відомі дві сторони,  та кут
та кут 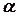 між векторами
між векторами 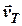 та
та 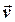 , тому за теоремою синусів знаходимо кут
, тому за теоремою синусів знаходимо кут 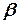 , який спирається на
, який спирається на 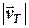 і визначає зміну курсу за рахунок течії. Для визначення абсолютної швидкості
і визначає зміну курсу за рахунок течії. Для визначення абсолютної швидкості 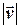 знову застосовуємо теорему синусів.
знову застосовуємо теорему синусів.
Приклад. Знайти величину абсолютної швидкості 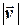 та істинний курс
та істинний курс 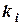 , щоб судно рухалось заданим шляховим кутом
, щоб судно рухалось заданим шляховим кутом 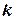 = 220° в області дії тієї ж самої течії, що у попередньому прикладі, якщо модуль відносної швидкості
= 220° в області дії тієї ж самої течії, що у попередньому прикладі, якщо модуль відносної швидкості  відомий (нехай має таке значення, як у прямій задачі).
відомий (нехай має таке значення, як у прямій задачі).
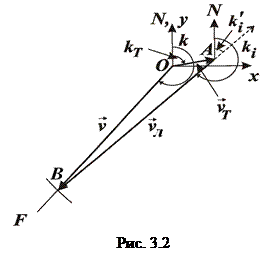 Розв’язання. Графічний метод. Вважаємо, що судно знаходиться у точці
Розв’язання. Графічний метод. Вважаємо, що судно знаходиться у точці  . Від норду відкладаємо шляховий кут
. Від норду відкладаємо шляховий кут  і проводимо лініюшляху
і проводимо лініюшляху  , по якій повинно рухатися судно (рис. 3.2). Вектор абсолютної швидкості судна
, по якій повинно рухатися судно (рис. 3.2). Вектор абсолютної швидкості судна 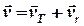 повинен співпадати з лінією шляху
повинен співпадати з лінією шляху 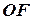 . Для того, щоб знайти напрям вектора
. Для того, щоб знайти напрям вектора 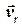 (істинний курс
(істинний курс 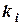 ) послідовно виконаємо наступні операції:
) послідовно виконаємо наступні операції:
1) з початкової точки 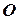 побудуємо вектор швидкості течії
побудуємо вектор швидкості течії 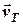 у обраних раніше масштабах (1 см = 1 миля, 1 см = 1 вузол) та отримаємо точку
у обраних раніше масштабах (1 см = 1 миля, 1 см = 1 вузол) та отримаємо точку 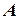 (рис. 3.2), в яку течія за одну годину зносить судно з умовно виключеним двигуном;
(рис. 3.2), в яку течія за одну годину зносить судно з умовно виключеним двигуном;
2) умовно відключаємо течію і визначаємо, куди може потрапити судно за такий самий час з точки 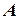 у відсутності течії під дією двигуна. Таким геометричним місцем точок буде коло з центром у точці
у відсутності течії під дією двигуна. Таким геометричним місцем точок буде коло з центром у точці 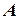 , радіус якого дорівнює модулю швидкості судна відносно нерухомої води, тобто
, радіус якого дорівнює модулю швидкості судна відносно нерухомої води, тобто 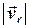 . Тому з точки
. Тому з точки 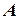 циркулем з розтином
циркулем з розтином 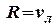 робимо помітку на лінії шляху
робимо помітку на лінії шляху 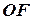 і отримаємо точку
і отримаємо точку 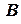 . Напрям
. Напрям 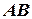 відносно норду визначає істинний курс судна
відносно норду визначає істинний курс судна 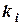 (дивись рис. 3.2), а довжина відрізку
(дивись рис. 3.2), а довжина відрізку 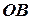 , який розташований на лінії шляхового кута, визначає модуль вектора абсолютної швидкості
, який розташований на лінії шляхового кута, визначає модуль вектора абсолютної швидкості 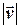 .
.
Вимірюємо довжину 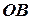 і отримуємо модуль абсолютної швидкості
і отримуємо модуль абсолютної швидкості 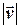 = 13,6 вузлів. Вимірюємо істинний курс і отримуємо
= 13,6 вузлів. Вимірюємо істинний курс і отримуємо 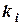 = 227°, який повинно тримати судно, щоб рухатися заданим шляховим кутом
= 227°, який повинно тримати судно, щоб рухатися заданим шляховим кутом 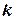 = 220°. Отже, поправка на течію
= 220°. Отже, поправка на течію 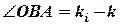 = 7°.
= 7°.
Аналітичний метод розв’язання базується на властивостях трикутників. Так, у трикутнику швидкостей 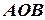 (дивись рис. 3.2) відомі дві сторони
(дивись рис. 3.2) відомі дві сторони 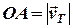 ,
, 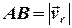 та кут
та кут 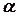 =
= 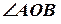 між векторами
між векторами 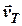 та
та 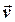 легко знаходиться з умови задачі
легко знаходиться з умови задачі 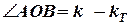 = 140°. Тоді за теоремою синусів знаходимо кут
= 140°. Тоді за теоремою синусів знаходимо кут 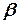 =
= 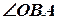 , який потрібно знайти для визначення істинного курсу:
, який потрібно знайти для визначення істинного курсу:
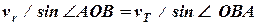
звідки отримуємо рівняння для визначення кута 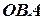 :
:
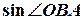 =
= 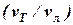 ·
· 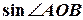 = 0,1205,
= 0,1205,
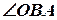 =
= 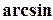 (0,1205) = 6,9°.
(0,1205) = 6,9°.
Тоді для істинного курсу в конкретній ситуації (рис. 3.2) отримуємо
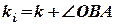 = 227°.
= 227°.
Для визначення абсолютної швидкості 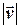 знову застосовуємо теорему синусів, оскільки кут на який спирається цей вектор
знову застосовуємо теорему синусів, оскільки кут на який спирається цей вектор 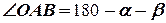 = 33°
= 33°
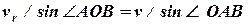 ,
,
Звідки знаходимо
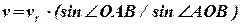 = 13,6 (вуз.).
= 13,6 (вуз.).
Таким чином, щоб судно рухалося шляховим кутом 220° в області дії даної течії необхідно, щоб його істинний курс був 227°, при цьому абсолютна швидкість буде 13,6 вузлів, а не 16 вузлів.
Відповідь: 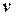 = 13,6 вузлів,
= 13,6 вузлів, 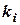 = 227°.
= 227°.
