Вычисление двойного интеграла

ДВОЙНОЙ ИНТЕГРАЛ

Определение, геометрический смысл и свойства двойного интеграла

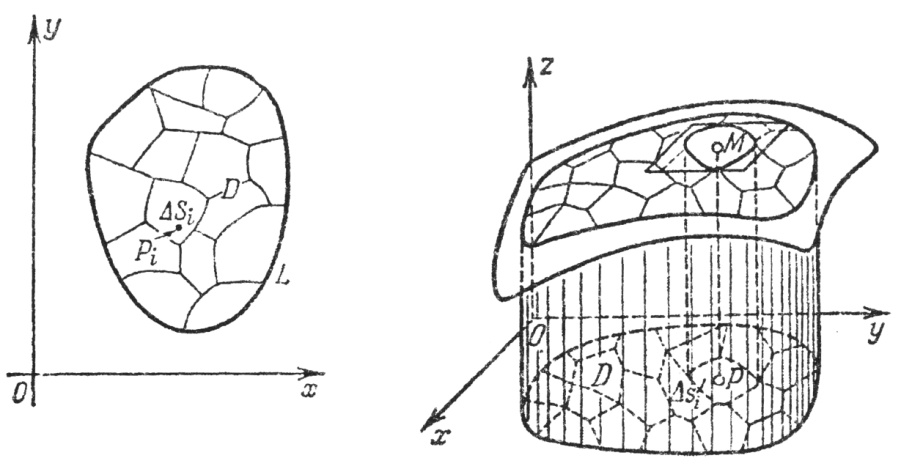
Рис.1 Рис.2

Пусть в плоскости 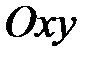задана область D, ограниченная линией L (рис. 1).

Пусть в области D задана непрерывная функция Разобьём об­ласть D на n-площадок: В каждой из площадок возьмём точку Pi, тогда значение функции в каждой точке будет равно 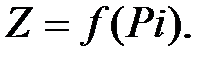Составим интегральную сумму для функции 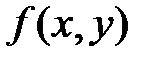в области D:

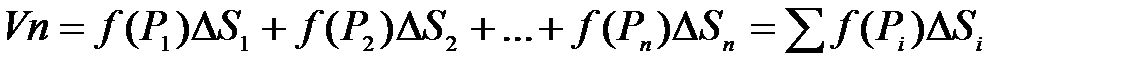(1)

Если 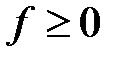в области D, то каждое слагаемое 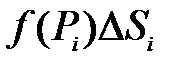можно представить геометрически как объём малого цилиндра, основание которого есть 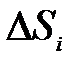, а вы­сота 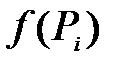. Сумма есть сумма объёмов элементарных цилиндров (рис. 2). Предположим, что при 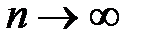максимальный диаметр площадок 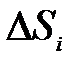стремится к 0.

Теорема 1. Если функция 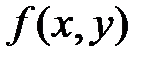непрерывна в замкнутой области D, то существует предел последовательности интегральных сумм (1), если макси­мальный диаметр площадок 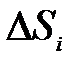стремится к нулю при 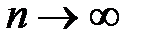. Этот предел не за­висит от способа разбиения области D на площадки 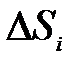, ни от выбора точки 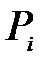внутри площадки .

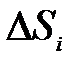Определение. Этот предел называется двойным интегралом от функции 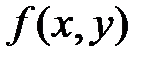по области D и обозначается

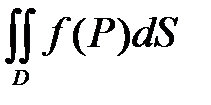или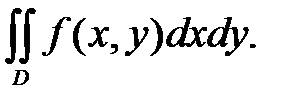

Т.е. 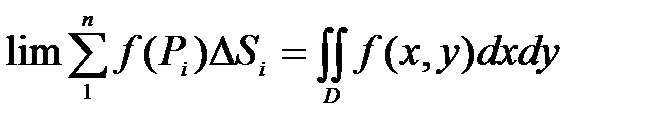область D - называется областью интегрирования.

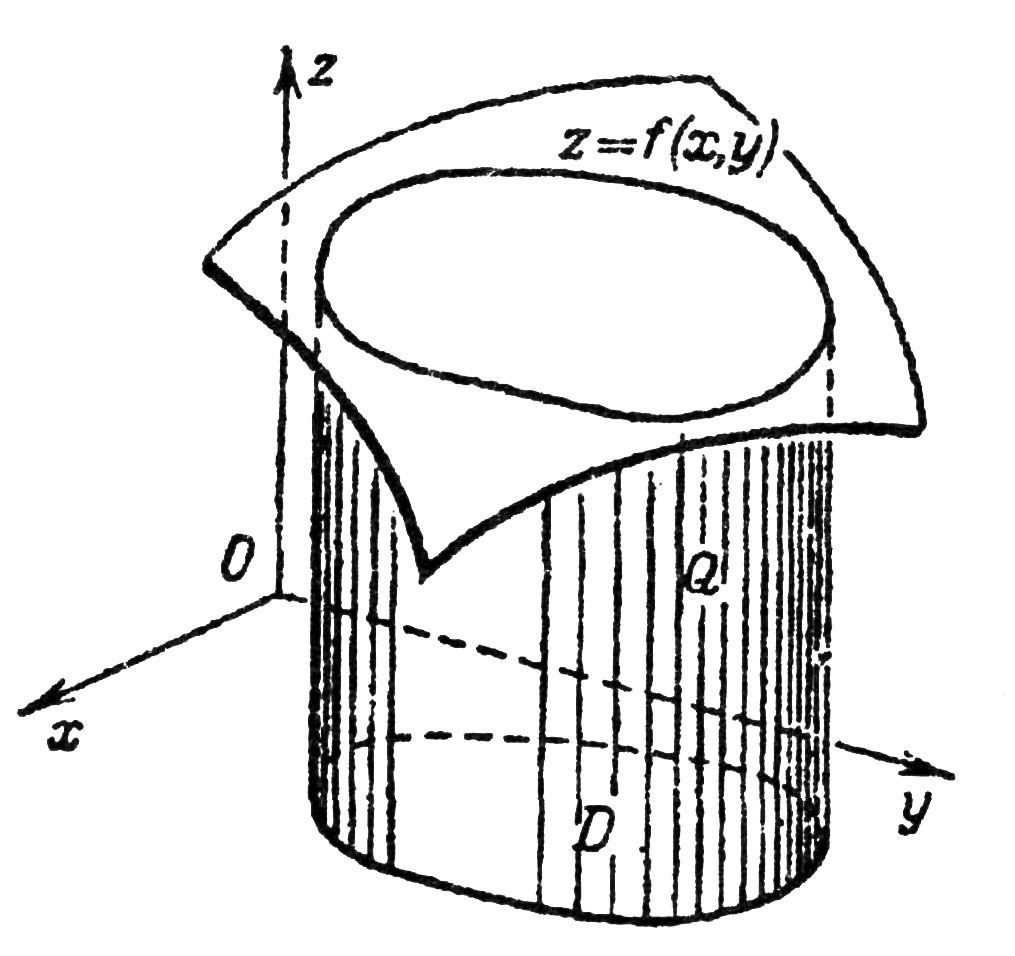
Геометрический смысл двойного интеграла. Если 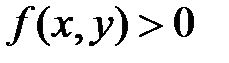, то двойной интеграл от функции 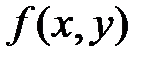по области D равен объёму тела, ограниченного по­верхностью 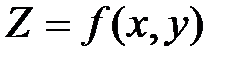, плоскостью 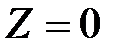и цилиндрической поверхностью, обра­зующие которой параллельны оси 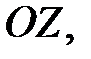а направляющей служит граница области D (рис. 3).

Свойства двойного интеграла:

1. Двойной интеграл от суммы двух функций 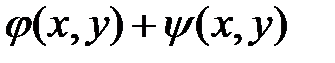по области D равен сумме двух двойных интегралов по облас­ти D от каждой из функций в отдельности:

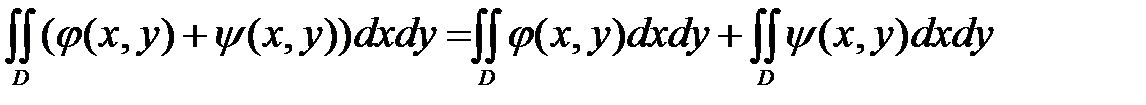
Рис.3

2. Постоянный множитель можно вынести за знак интеграла: если 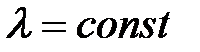, то

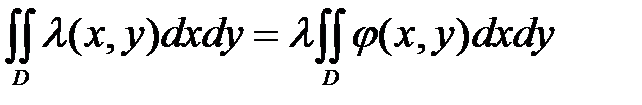
3. Если область D разбить на две области D, и D₂ без общих внутренних точек, и функция 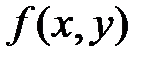непрерывна во всех точках области D, то

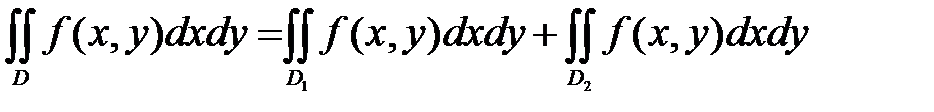
Вычисление двойного интеграла

Введем понятие правильной области в направлении оси ОУ: Пусть в плоско­сти ОХУ задана область D, ограниченная линиями 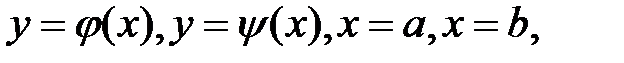причём 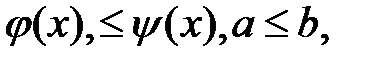а функции 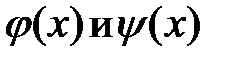непрерывны на отрезке 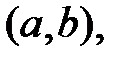и лю­бая прямая, проведённая через область D, параллельная оси ОУ, пересекает гра­ницу области в двух точках (рис. 4). Область D будет называться правильной в направлении оси ОХ. Аналогично определяется область, правильная в направ­лении оси ОХ: Область D будет правильной в направлении оси ОХ, если она ог­раничена линиями 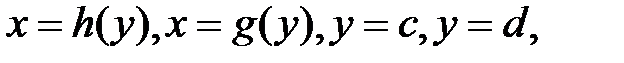причём 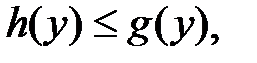а функции 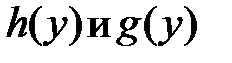непрерывны на отрезке 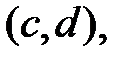и любая прямая, проведённая через область D, параллельно оси ОХ, пересекает границу области в двух точках (рис. 5).

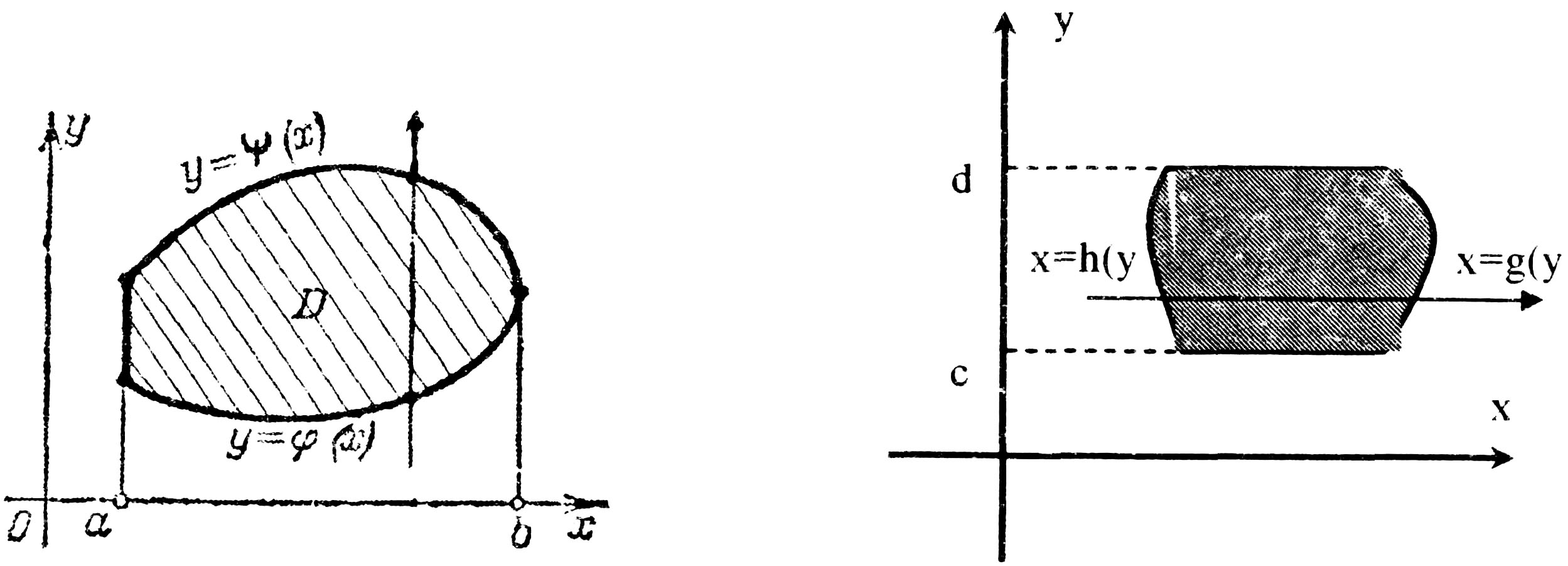
Рис.4 Рис.5

Определение. Если 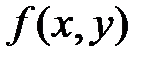непрерывна в области D, то выражение 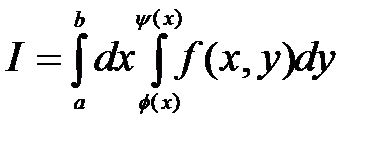называется двукратным интегралом от функции 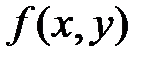по области D.

Вычисление повторного интеграла. Сначала вычисляется внутренний ин­теграл, причём интегрирование производится по у, а х считается постоянным. В результате получим непрерывную функцию от х

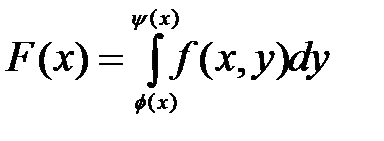
Далее вычисляют внешний интеграл

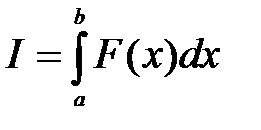
1.3. Вычисление двойного интеграла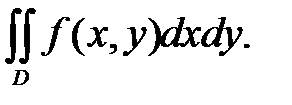

1. Изобразим в координатной плоскости ОХУ область D.

2. От двойного интеграла перейдём к повторному интегралу, расставляя пределы интегрирования.

Если область D правильная в направлении оси 0У, то двойной интеграл перейдёт в повторный интеграл такого вида:

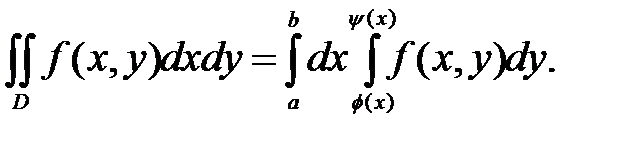(1.1)

Для того чтобы правильно расставить пределы интегрирования во внут­реннем интеграле, проведём прямую через область D параллельно оси 0У, нижняя граница, которую пересечёт прямая, будет нижним пределом интегри­рования 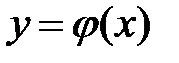, и верхняя граница области D, из которой выйдет прямая будет верхним пределом интегрирования 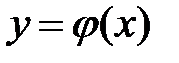. Пределы интегрирования во внут­реннем интеграле - это линии, заданные функциями, зависящими от х. Пределы интегрирования во внешнем интеграле определяются как пределы изменения области D вдоль оси ОХ. Пределы интегрирования во внешнем интеграле это - числа.

Если область D правильная в направлении оси ОХ. то двойной интеграл перейдёт в повторный интеграл такого вида:

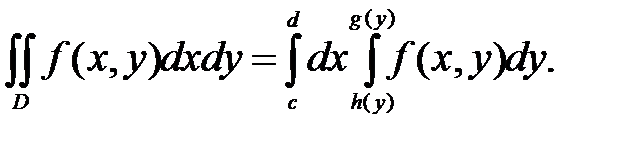(1.2)

Для того чтобы правильно расставить пределы интегрирования во внут­реннем интеграле, проведём прямую через область D параллельно оси ОХ. ниж­няя граница, которую пересечёт прямая, будет нижним пределом интегрирова­ния 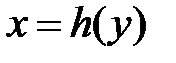, и верхняя граница области D, из которой выйдет прямая будет верхним пределом интегрирования 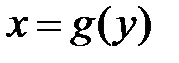. Пределы интегрирования во внут­реннем интеграле - это линии, заданные функциями, зависящими от у. Пределы интегрирования во внешнем интеграле определяются как пределы изменения области D вдоль оси OY. Пределы интегрирования во внешнем интеграле это -числа.

Примечание. Если область D - неправильная область, то её надо разбить на правильные области, и исходный двойной интеграл будет суммой двойных интегралов по этим областям.

3. Вычислить повторный интеграл.

Пример 1. Вычислить двойной интеграл

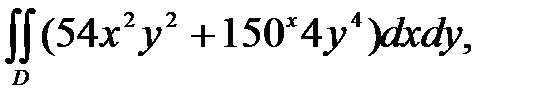
где область D ограничена линиями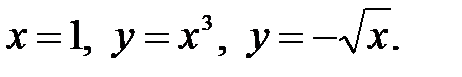

Решение.

1. Зададим область D неравенствами. Очевидно, что 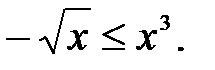Поэтому 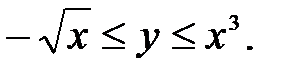Поскольку 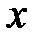фигурирует под знаком квадратного корн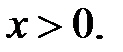я, Для 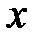возможны неравенства 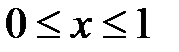или 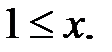Во втором случае область неограниченна, что неприемлемо.

Итак,

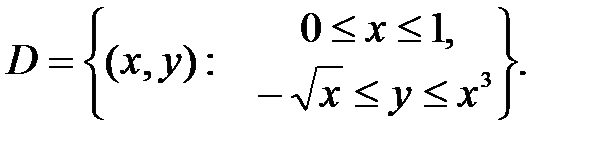
2. Переходим от двойного интеграла к повторному:

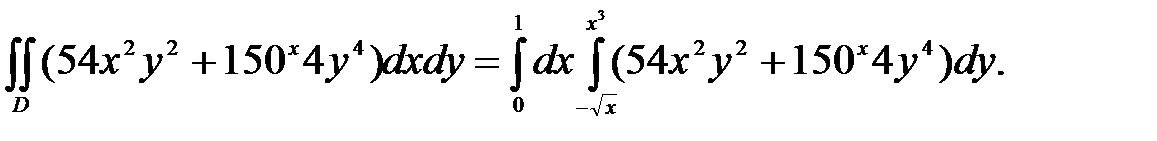
3. Используя свойства определенного интеграла, последовательно интегрируем сначала по y(считая х постоянной), затем по х:

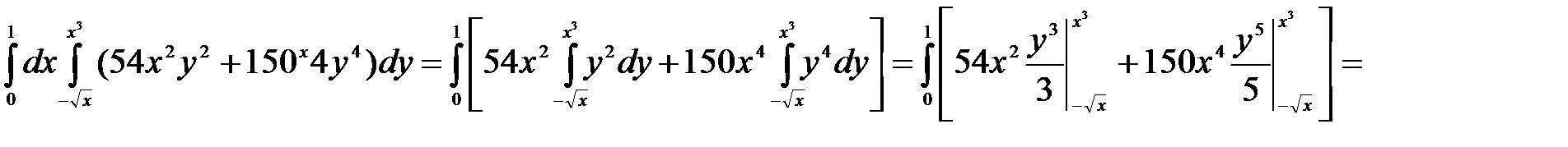
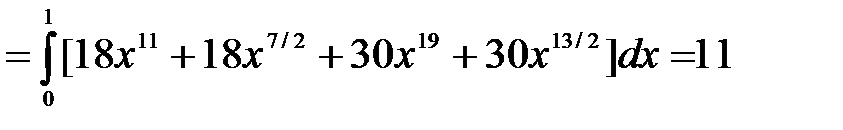
Пример 2. Расставить и вычислить двойной интеграл от функции 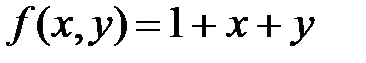по об­ласти D, ограниченной линиями: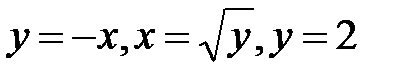

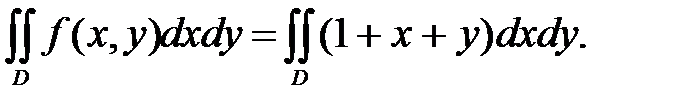
Решение. Сделаем рисунок области D (рис. 6).

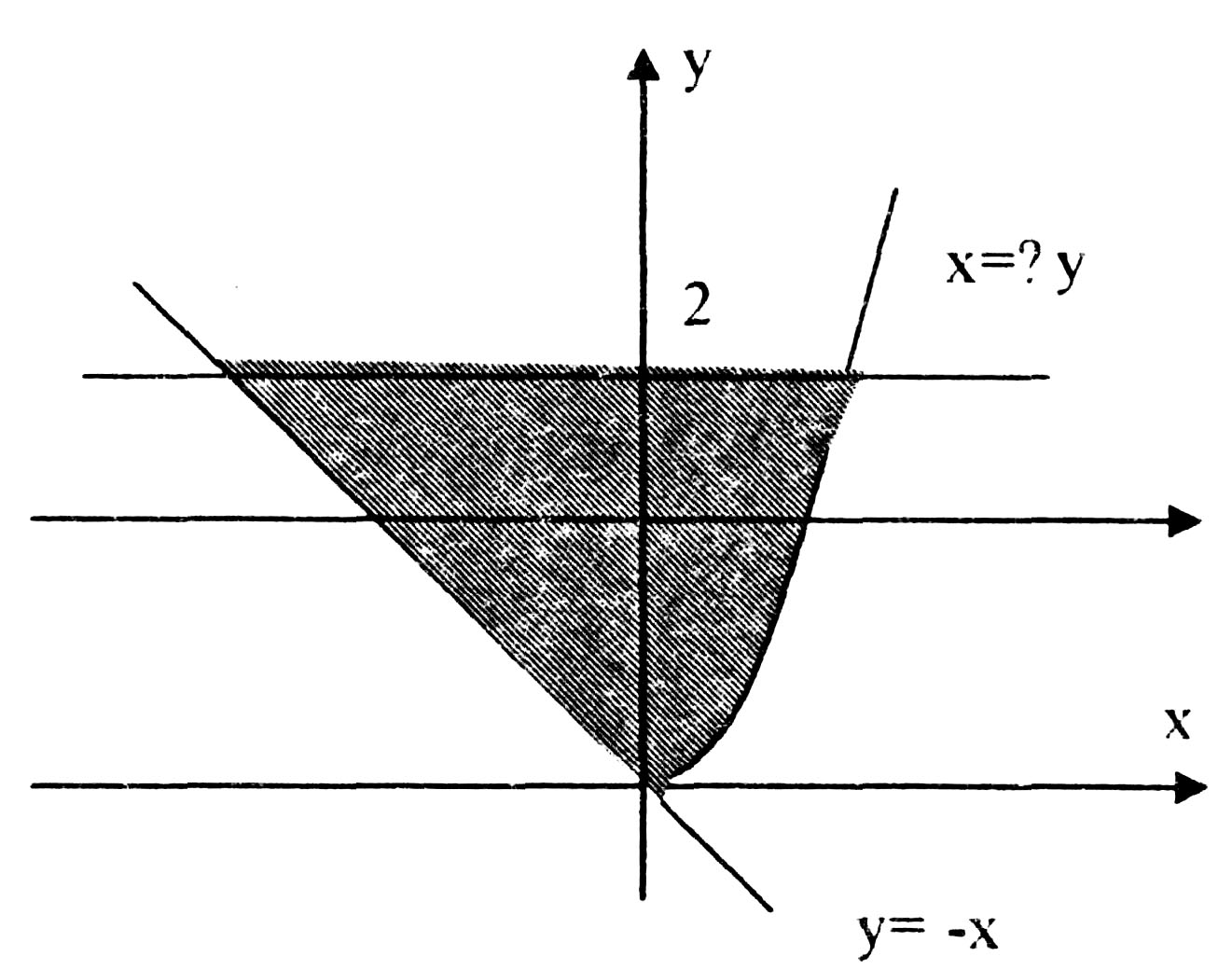
Рис. 6

Область D будет правильной в направлении оси ОХ. Проведём прямую через область D, параллельно оси ОХ, левая граница области D, которую пере­сечёт прямая: 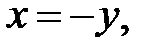а правая граница 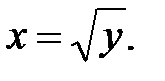Область D вдоль оси ОУ будет ме­няться от 0 до 2. От двойного интеграла перейдём к повторному:

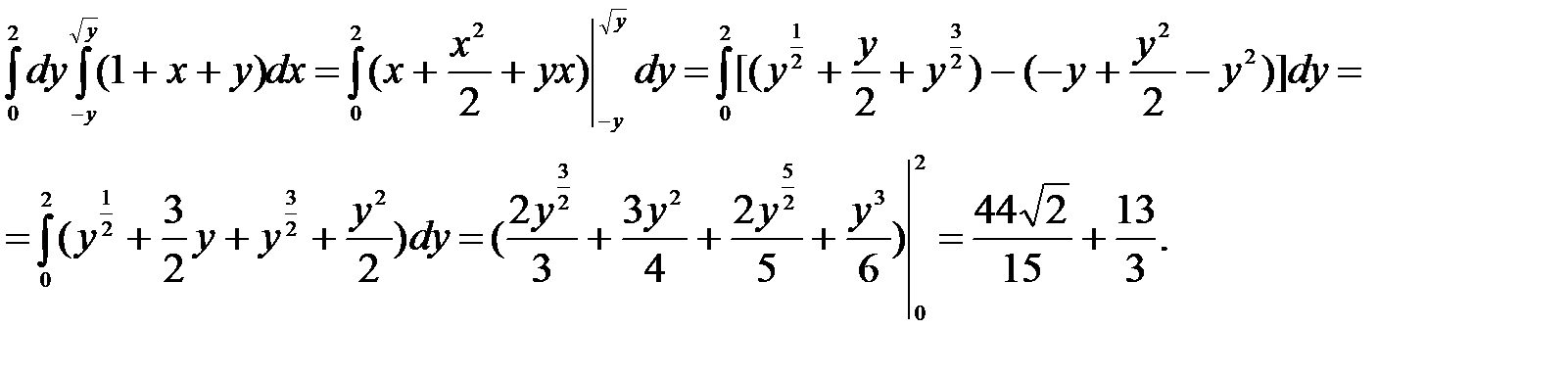
Пример 3. Вычислить двойной интеграл

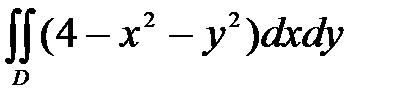. Область D ограничена прямыми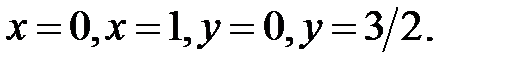

Решение:

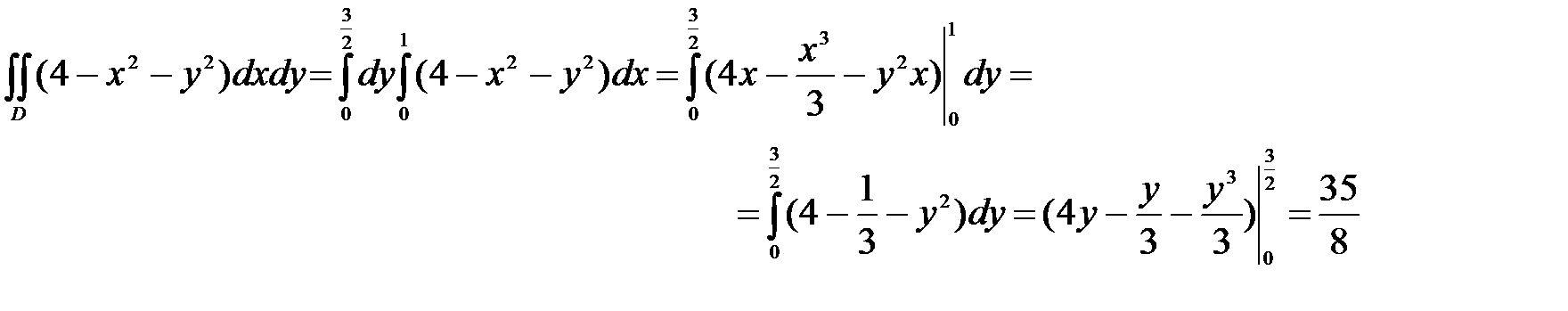Пример 4. Расставить пределы и вычислить двойной интеграл

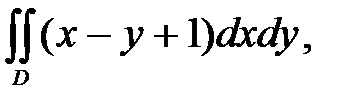где D: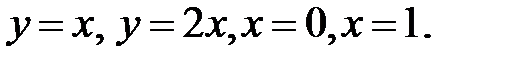

Решение:Сделаем рисунок области D (рис. 7). Область D – правильная в направлении оси OY.

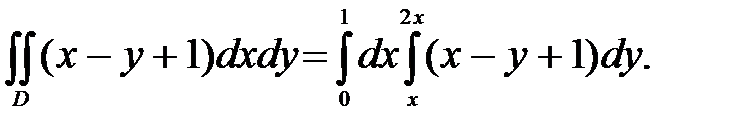
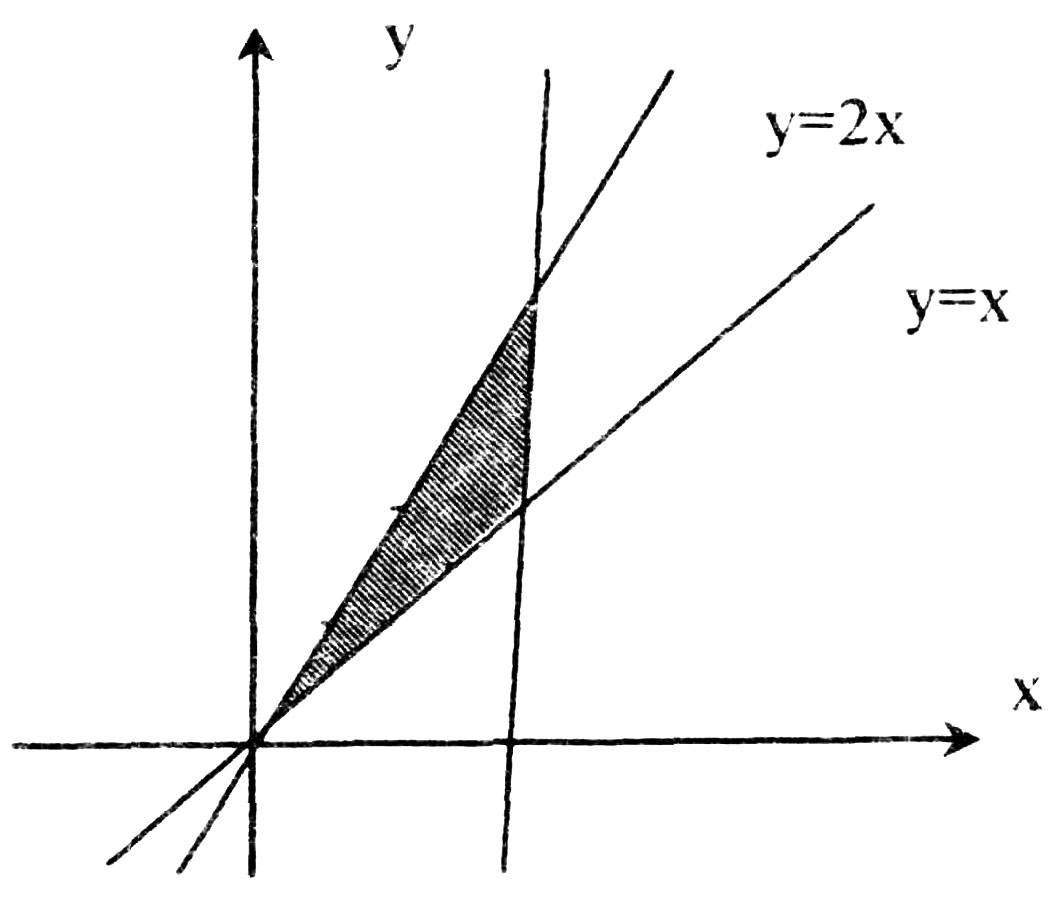
Рис. 7

Вычислим внутренний интеграл

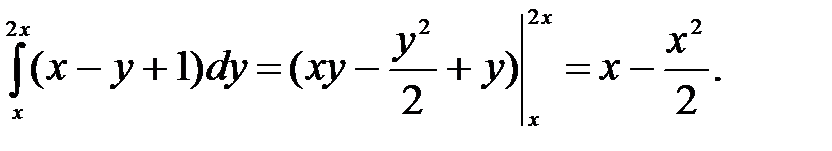
Вычислим внешний интеграл

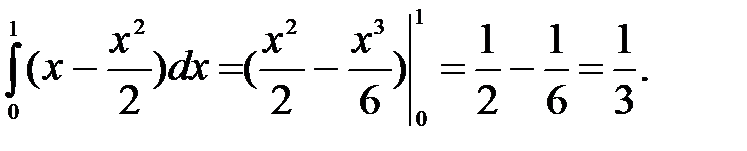
Пример 5. Вычислить двойной интеграл

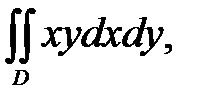где D: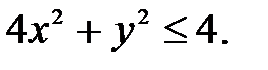

Решение. Построим область D (рис. 8). Это будет эллипс, будем интегри­ровать по х, найдём пределы внутреннего интеграла

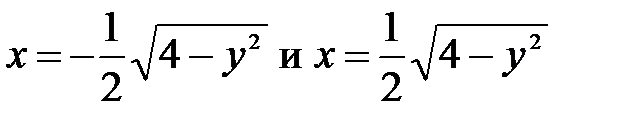
Пределы внешнего интеграла найдём как ординаты самой нижней и са­мой верхней точек области D: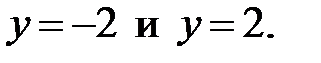

Перейдём от двойного интеграла к повторному

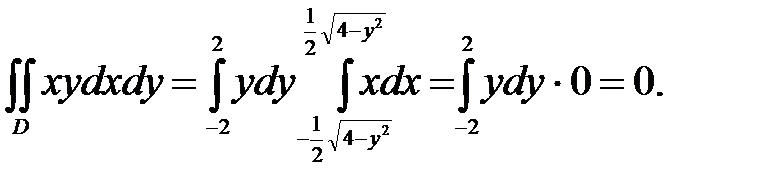
Пример 6. Вычислить двойной интеграл

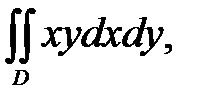где область D ограничена прямой 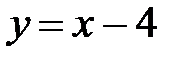и параболой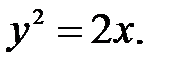

Решение. Построим область D (рис. 9), она будет правильная в направле­нии оси ОХ, от двойного интеграла перейдём к повторному

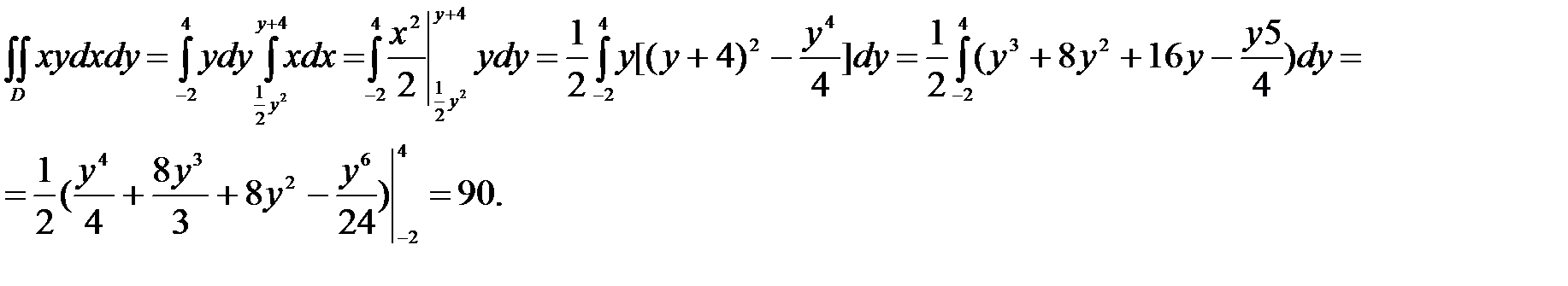
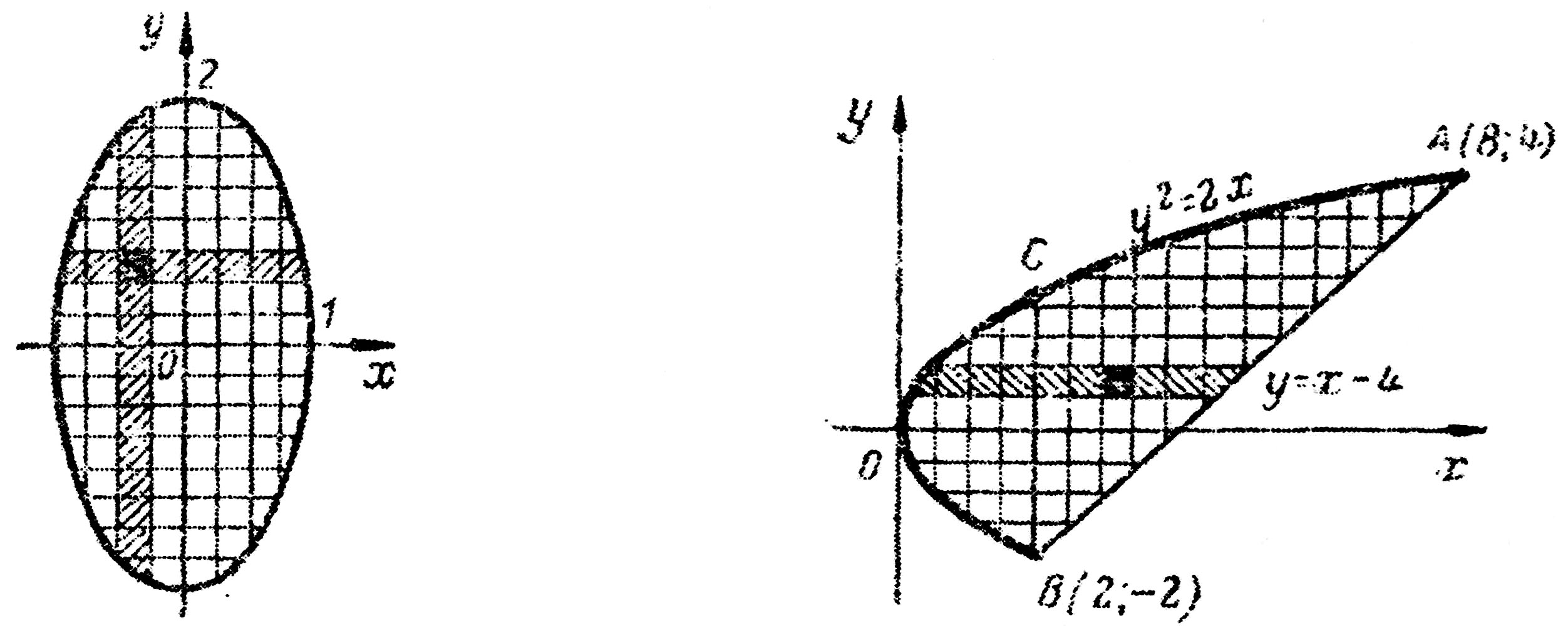
Рис. 8 Рис.8