Похибки при арифметичних діях з наближеними числами

Похибки при арифметичних діях з наближеними числами виражаються через похибки первісних величин на підставі властивостей, які приведемо без доказу.

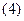1) Абсолютна похибка алгебраїчної суми декількох чисел дорівнює сумі абсолютних похибок доданків:

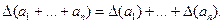
З (4) слідує, що якщо всі доданки a₁,...,а_п (незалежно від їхніх знаків) мають ту саму абсолютну похибку 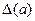, то

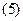
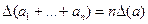
Однак при великій кількості доданків ця формула дає завищені результати, оскільки відхилення доданків від їхніх точних значень можуть мати різні знаки й у сумі великої кількості доданків частково компенсуватися. У теорії ймовірностей доводиться, що при великому п можна прийняти

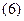
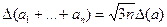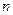( >10)

(правило Чеботарєва).

Приклад 4. У трикутнику дані сторони a=17,3 см, b=23,6 см, с = 14,2 см , причому 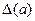= = 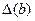= 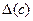0,1 см. Визначити його периметр р й .

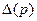Розв’язання: р = 17,3 + 23,6 + 14,2 = 55,1 (см). По формулі
(5) маємо 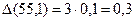(см). У числі р=55,1 остання цифра сумнівна. Результат можна записати у вигляді р = 55,1 ± 0,3 (см).

Ясно, що абсолютна похибка суми наближених чисел не менше найбільшої з абсолютних похибок доданків. Тому при обчисленні суми наближених чисел всі доданки варто округляти до кількості десяткових знаків числа з найбільшою абсолютною похибкою, залишаючи один сумнівний знак (а при великій кількості доданків - два). Отриманий результат округляється на один знак.

2) Відносна похибка суми декількох чисел визначається, на підставі (2), по формулі

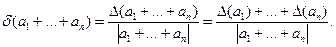
Якщо а₁,...,а_п—числа одного знаку, то відносна похибка 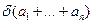укладена між найменшою й найбільшою з відносних похибок доданків:

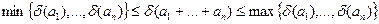
Так, у попередньому прикладі

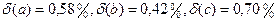й

.

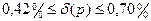У дійсності

.

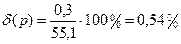При вирахуванні двох чисел одного знака відносна похибка різниці

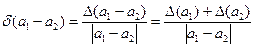
може виявитися значно більше відносних похибок кожного з даних чисел. Це в основному буває, якщо |а₁ — а₂| — мале число.

Приклад 5. Обчислити абсолютну й відносну похибки різниці чисел а₁=9,78, 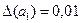і а₂=9,22, .

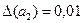Розв’язання: а₁-а₂=0,56, 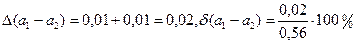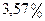, хоч , .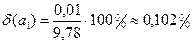

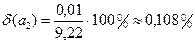Звичайно вирахування близьких чисел намагаються уникати, заміняючи його по можливості іншими діями.

3) Відносна похибка добутку декількох чисел дорівнює сумі відносних похибок співмножників:

.

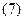
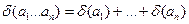Абсолютна похибка добутку обчислюється по формулі (3)

.

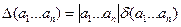Зокрема, якщо в добутку са число с точне, то 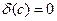и

.

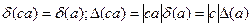Звідси й з формули (4) одержуємо

.

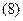
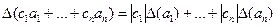4) Відносна похибка частки дорівнює сумі відносних похибок діленого й дільника:

.

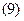
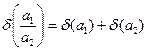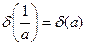Зокрема,

Абсолютну похибку частки визначають по формулі (3).

Якщо кількість чисел у добутку або відношенні велика, а відносна похибка кожного числа приблизно однакова (дорівнює 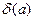), то, аналогічно формулі (6), відносна похибка результату обчислюється по формулах

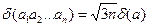(n > 10),

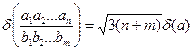(n+m>10).

При наявності декількох співмножників, в одного із яких відносна похибка у багато разів більше, ніж в інших (він обчислений найменш точно), відносна похибка добутку буде визначатися саме по цій похибці. Тому число вірних знаків в інших співмножників треба вибирати по найменш точному числу, залишаючи один сумнівний. Аналогічно надходимо й при діленні.