Уравнение прямой в нормальной форме. Расстояние от точки до прямой

Определение. Говорим, что общее уравнение прямой

Ax + By + C = 0 , (14)

имеет нормальную форму, если A²+B ² = 1. Это равносильно тому, что вектор (A, B) – единичный.

Если уравнение (14) не имеет нормальной формы, то мы можем привести его к этой форме, разделив на :

x + y + = 0.

Тогда ²+ ²= 1.

Теорема 3. Пусть прямая l определяется уравнением (14) в нормальной форме. Тогда расстояние от точки M(x₁, y₁) до прямой вычисляется по формуле

h =½Ax₁+ By₁+ C½ . (17)

Следствие. Если прямая определяется произвольным уравнением вида (14), то

h = . (17¢ )

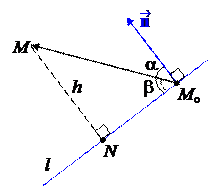
Доказательство. Пусть (A, B) – вектор нормали к l. Поскольку уравнение имеет нормальную форму, то ½½ = 1. Пусть M_o(x_o, y_o) – произвольная точка на прямой. Опустим перпендикуляр MN

на прямую l . Пусть a =Ð( , ), b =ÐMM_oN .

1 случай. Точка M и вектор лежат в одной полуплоскости относительно прямой l. Тогда

h =½MN½=½MM_o½·sin b =½½·sin( – a) =

=½½·cos a·½½= ·

(мы домножили на ½½, поскольку эта величина равна единице). Находим, что (x₁– x_o, y₁– y_o) Þ

h = A(x₁– x_o) + B(y₁– y_o) = Ax₁+By₁+C – (Ax_o+By_o+C)

(мы добавили и отняли C ). Поскольку M_oÎ l, то выражение в скобках равно нулю, и мы получаем

h = Ax₁+ By₁+ C.

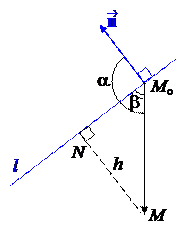2 случай. Точка M и вектор лежат в разных полуплоскостях относительно прямой l. Тогда b = a – p/2 Þ sin b = – cos a и те же самые вычисления дают

h = – · = –Ax₁ – By₁ – C.

Поскольку h – это расстояние, то h ³ 0. Это

значит, что во втором случае Ax₁+ By₁+ C < 0 (равенство исключается, т.к. MÏ l). Поэтому

h =½Ax₁+ By₁+ C½ .

Эта формула подойдет и к первому случаю.

Попутно мы выяснили, что знак выражения Ax₁+ By₁+ C зависит от того, в какой полуплоскости находится точка M. Это позволяет для двух данных точек M₁, M₂ выяснить, лежат ли они в одной полуплоскости относительно прямой l или в разных (Û пересекает отрезок M₁M₂ прямую l или нет).

§5. Уравнение прямой в полярных координатах.

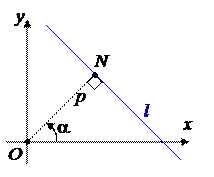
Пусть на плоскости заданы прямая l и полярная система координат, OP – полярная ось. Опустим перпендикуляр ON из полюса на прямую l. Обозначим p =½ON½ – его длина, a – ориентированный угол между OP и ON. Пусть M(r, j) – произвольная точка прямой.

Тогда из DOMN находим

p = r·cos(a – j) или p = r·cos(j – a). (18)

Поскольку косинус четная функция, то достаточно только первого уравнения.

Обратно, если координаты точки M(r, j) удовлетворяют (18), то DOMN – прямоугольный Þ MÎ l.

Итак, (18) представляет собой уравнение прямой в полярных координатах.

Введем теперь декартову СК так, чтобы Ox­­ OP. Уравнение (18) можно переписать так:

r cos j cos a + r sin j sin a – p = 0.

Согласно формулам перехода r·cos j = x, r·sin j = y Þ

x cos a + y sin a – p = 0. (19)

Это уравнение называют нормальным уравнением прямой. Еще раз отметим геометрический смысл используемых в этом уравнении параметров: p – это длина перпендикуляра, опущенного из начала координат на прямую, а a – ориентированный угол между осью Ox и этим перпендикуляром. Поскольку cos²a + sin²a = =1, то это уравнение имеет нормальную форму, как это было определено в предыдущем параграфе.

Упражнение. Пусть две прямые заданы своими уравнениями в полярных координатах: l₁: p₁ = r·cos(a₁ – j), l₂: p₂ = r·cos(a₂ – j). Выпишите условия параллельности и совпадения этих прямых, а также найдите угол между ними. Найдите, чему равно расстояние между l₁ и l₂, если они параллельны.

Пучок прямых.

Пусть две несовпадающие прямые на плоскости заданы своими общими уравнениями:

l₁: A₁x + B₁y + C₁ = 0 ,

l₂: A₂ x + B₂y + C₂ = 0 .

Рассмотрим совокупность всех прямых, которые задаются различными уравнениями вида

(lA₁+mA₂) x + (lB₁+mB₂) y + lC₁+ mC₂ = 0, (20)

где l и m – числа не равные нулю одновременно. Это множество называется пучком прямых. Очевидно, при l = 1, m = 0 мы получим уравнение прямой l₁, а при l = 0, m = 1 – уравнение прямой l₂. Таким образом, прямые l₁ и l₂ тоже входят в пучок.

Теорема 4. 1.Если прямые l₁ и l₂ пересекаются в точке M_o, то определяемый ими пучок прямых, состоит из всех прямых, проходящих через M_o.

2. Если l₁½½ l₂ , то определяемый этими прямыми пучок состоит из всех параллельных им прямых.

Доказательство. 1.Перепишем (20) в виде

l(A₁x + B₁y + C₁) + m(A₂ x + B₂ y + C₂) = 0. (20¢)

Пусть M_o(x_o, y_o) = l₁I l₂. Тогда ее координаты удовлетворяют уравнениям обеих прямых. Подставим ее координаты в (20¢):

l(A₁x_o+ B₁y_o+ C₁) + m(A₂ x_o+ B₂ y_o+ C₂) = 0.

Поскольку обе скобки должны быть равны нулю, то мы получаем верное равенство независимо от l и m. Таким образом, все прямые пучка (20) проходят через M_o.

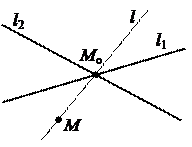Покажем, что в пучок входят все прямые, проходящие через M_o. Пусть M(x₁, y₁) – произвольная точка плоскости, отличная от M_o. Подставим ее координаты в (20¢) и обозначим

X= A₁x₁+ B₁y₁+ C₁, Y = A₂ x₁+ B₂ y₁+ C₂.

Получим уравнение

lX + mY= 0 (*)

относительно неизвестных l и m. Это уравнение всегда имеет решение (l_o, m_o). При l=l_o и m=m_o уравнение (20) будет задавать прямую, проходящую через M.

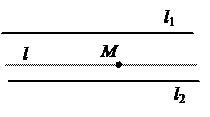2. Пусть l₁½½ l₂ . Тогда выполнено

= = k .

Пусть l – произвольная прямая из пучка (20). Применим к ней признак параллельности с прямой l₂:

= Û l + m = l + m Û lk + m = lk + m ,

т.е. имеем верное равенство. Значит l½½ l₂ .

Покажем, что в пучок входят все прямые параллельные l₁ и l₂. Пусть M(x₁, y₁) – произвольная точка плоскости, не лежащая ни на l₁ , ни на l₂. Подставив ее координаты в (20¢) также получим уравнение (*) относительно неизвестных l и m , где X и Y оба ненулевые. При l и m , удовлетворяющих (*) уравнение (20) будет задавать прямую, проходящую через M.

Если все прямые пучка пересекаются в точке M_o, то точка M_o называется центром пучка, и пучок прямых называется собственным или центральным. Если все прямые пучка параллельны друг другу, то пучок называется нецентральным или несобственным.