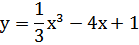Производная сложной функции

Пусть переменная y является функцией от переменной u ( 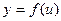), а переменная u в свою очередь является функцией от независимой переменной х 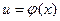, тесть задана сложная функция .

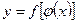Правило. Если 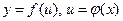- функции, имеющие производные, то производная сложной функции равна производной данной функции 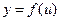по промежуточному аргументу ии умноженной на производную самого промежуточно­го аргумента 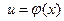по независимой переменной х, т.е

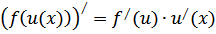
Тогда таблица производных для сложных функций будет выглядеть

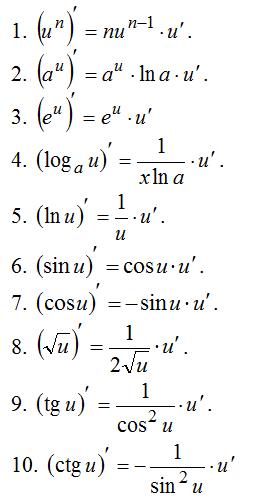
Пример

а) .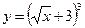

Функцию представим в ви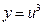де , где .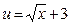

Тогда на основании дифференцирования сложной функции

;

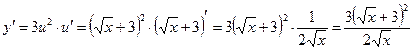б)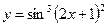

Пусть 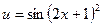, тогда .

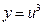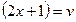, тоді .

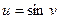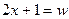, тоді .

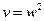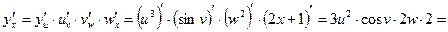
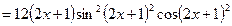
Обычно при дифференцировании сложную функцию не раскладывают на простые, а дифференцируют таким образом

.

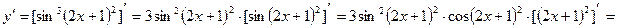
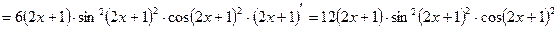4. Алгоритм составления уравнения касательной к графику функции y = f(x)

1. Обозначить буквой х₀ абсциссу точки касания.

2. Найти f(х₀).

3. Найти f '(x) и f '(х₀).

4. Подставить найденные числа х₀, f(х₀), f '(х₀) в общее уравнение касательной

y - f(х₀) = f '(х₀)(x – х₀).

Пример. Составьте уравнение касательной в точке M(3; – 2) к графику функции