Лекция 5. Элементы математической статистики
1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА
Дано большое множество, содержащее  объектов, называемое генеральной совокупностью объёма
объектов, называемое генеральной совокупностью объёма  Из него вы отбираете
Из него вы отбираете  объектов с целью получить представление о том, какими качествами обладает генеральная совокупность. Это множество называется выборкой объёма
объектов с целью получить представление о том, какими качествами обладает генеральная совокупность. Это множество называется выборкой объёма 
Отбор может быть
- повторным, когда выбранный и обследованный объект возвращается в генеральную совокупность и поэтому может попасться при повторном отборе;
- бесповторным, когда объект не возвращается.
Математическая статистика – раздел математики, в котором даются методы обработки результатов наблюдений с целью получить представление о свойствах, качествах генеральной совокупности.
2. ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ
Пусть в выборке объёма  вы наблюдали
вы наблюдали  значений СВ
значений СВ 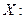
 Эти числа называются вариантами. Расположим их в возрастающем порядке. Если среди этих чисел имеются одинаковые, например,
Эти числа называются вариантами. Расположим их в возрастающем порядке. Если среди этих чисел имеются одинаковые, например,  встречается
встречается  раз,
раз,  встречается
встречается  раз и т. д., то их объединяют и составляют вариационную таблицу
раз и т. д., то их объединяют и составляют вариационную таблицу
 |     |
 |     |

Числа  называются частотами. Если эта таблица оказывается длинной, рисуете интервал
называются частотами. Если эта таблица оказывается длинной, рисуете интервал  охватывающий все значения
охватывающий все значения 

 (рис. 2.1).
(рис. 2.1).

Рис. 2.1
Теперь разбиваете  на
на  частей и строите интервальную таблицу
частей и строите интервальную таблицу
| Интервалы |     |
| Частоты |     |
в которой  количество тех чисел
количество тех чисел  которые попали в интервал
которые попали в интервал  и т. д.
и т. д.
Количество интервалов  можно найти по формуле Стэрджеса
можно найти по формуле Стэрджеса

Ширина каждого интервала будет равна
 .
.
Зная частоты  можно найти относительные частоты
можно найти относительные частоты

Интервальная таблица позволяет построить гистограмму – фигуру, состоящую из прямоугольников с основаниями  и высотами
и высотами  (рис. 2.2).
(рис. 2.2).


Рис. 2.2 Рис. 2.3
Вариационная и интервальная таблица позволяют построить график эмпирической функции распределения

Для непрерывной СВ форма гистограммы обычно похожа на график плотности вероятности, поэтому по форме гистограммы можно выдвинуть гипотезу о законе распределения СВ. Этот закон называется теоретическим законом распределения СВ, математической моделью СВ или сглаживающей кривой.
3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЗАКОНА РАСПРЕДЕЛЕНИЯ
Искомыми параметрами (или характеристиками) генеральной совокупности обыч-но являются математическое ожидание 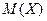 и среднеквадратичное отклонение
и среднеквадратичное отклонение  Их приближённое значение, их оценку можно найти с помощью вариацион-ной или интервальной таблицы.
Их приближённое значение, их оценку можно найти с помощью вариацион-ной или интервальной таблицы.
Приближённым значением вероятности (генеральной доли) являетсяотносительная частота(выборочная доля)

Приближённым значением генеральной средней 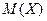 является выборочная средняя
является выборочная средняя

где  середины интервалов, если дана интервальная таблица (т. е.
середины интервалов, если дана интервальная таблица (т. е.  см. рис. 2.1). Верхняя черта означает усреднение величины.
см. рис. 2.1). Верхняя черта означает усреднение величины.
Приближённым значением генеральной дисперсии  является величина
является величина


которую можно преобразовать к виду
 ,
,
где
 .
.
Значение  называют также несмещённой оценкой выборочной дисперсииили исправленной выборочной дисперсией.
называют также несмещённой оценкой выборочной дисперсииили исправленной выборочной дисперсией.
Величина  называется исправленным выборочным среднеквадратичным отклонением или несмещённой оценкой выборочного среднеквадратичного отклонения.
называется исправленным выборочным среднеквадратичным отклонением или несмещённой оценкой выборочного среднеквадратичного отклонения.
Приближённым значением генеральной ковариации  является величина
является величина

в которой



4. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
Найденные по предыдущим формулам приближённые значения могут отличаться от точных, истинных значений. Чтобы получить представление о том, как далеко отклоняются приближённые значения от истинных, служат доверительные интервалы.
Доверительным интервалом для какого-либо параметра  называется числовой интервал
называется числовой интервал  накрывающий неизвестное истинное значение
накрывающий неизвестное истинное значение  с заранее заданной вероятностью
с заранее заданной вероятностью 
Число  называется доверительной вероятностью или надёжностью. В расчётах обычно берут
называется доверительной вероятностью или надёжностью. В расчётах обычно берут  или
или  Для математического ожидания и среднеквадратичного отклонения доверительный интервал находится так:
Для математического ожидания и среднеквадратичного отклонения доверительный интервал находится так:
Доверительный интервал для 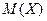 : :  . . | Доверительный интервал для   при при   при при  |
В этих формулах для повторной выборки
 |  |
а для бесповторной выборки
 |   |
Значение  можно взять из приложения 3 (Гмурман). можно взять из приложения 3 (Гмурман). | Значение  можно взять из приложения 4 (Гмурман). можно взять из приложения 4 (Гмурман). |
Длина доверительного интервала уменьшается с ростом  и увеличивается с ростом
и увеличивается с ростом 
5. ПРОВЕРКА СТАТИСТИЧЕСКОЙ ГИПОТЕЗЫ.
КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
Статистическая гипотеза – любое предположение о виде закона распределения или о его параметре.
Правило, по которому гипотеза отвергается или принимается, называется статистическим критерием.
Вероятность отвергнуть верную гипотезу называется уровнем значимости критерия и обозначается 
Обычно в расчётах берут  или
или  Если, например,
Если, например,  то мы в среднем 10 раз из 100 будем ошибочно отбрасывать верную гипотезу.
то мы в среднем 10 раз из 100 будем ошибочно отбрасывать верную гипотезу.
Для проверки гипотезы о виде закона распределения чаще всего применяется критерий согласия Пирсона (или критерий хи-квадрат), который заключается в следующем.
Пусть вы хотите проверить гипотезу о том, что СВ 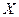 имеет закон распределения
имеет закон распределения 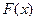 (это должен быть конкретный закон, скажем,
(это должен быть конкретный закон, скажем, 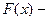 нормальный закон). Для этого вы задаёте какой-либо уровень значимости
нормальный закон). Для этого вы задаёте какой-либо уровень значимости  (например,
(например,  ) и определяете число
) и определяете число  по формуле
по формуле

в которой вероятности  находятся по известной формуле
находятся по известной формуле

В частности, когда проверяется гипотеза о том, что 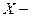 нормальная СВ (т. е. что
нормальная СВ (т. е. что 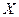 имеет нормальный закон распределения), то
имеет нормальный закон распределения), то
 .
.
Величина  характеризует отклонение функции распределения
характеризует отклонение функции распределения 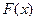 от эмпирической функции распределения
от эмпирической функции распределения 
Вычислив  затем из приложения 5 (Гмурман) находите критическое значение
затем из приложения 5 (Гмурман) находите критическое значение  в котором
в котором  (
(  число параметров функции распределения
число параметров функции распределения 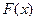 ).
).
Если выполняется условие    (критерий Пирсона), (критерий Пирсона), |
то гипотеза (о том, что СВ 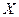 имеет закон распределения имеет закон распределения 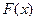 ) принимается, она согласуется с экспериментальными данными на уровне значимости ) принимается, она согласуется с экспериментальными данными на уровне значимости  |
6. ОПРЕДЕЛЕНИЕ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ
ПО ДАННЫМ ОПЫТА
Пусть вы наблюдали за двумя величинами 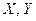 и результаты записали в таблицу
и результаты записали в таблицу
   |    | |
   |        |   и и     и и    |
     |    |
Эту таблицу называют корреляционной. Числа  заполняющие середину таблицы, называются частотами. Так, число
заполняющие середину таблицы, называются частотами. Так, число  означает, что пара
означает, что пара  наблюдалась
наблюдалась  раз.
раз.
Вычислив значения 
 строим точки
строим точки 
 и соединяем их (рис. 6.1). Получится линия, называемая линией регрессии
и соединяем их (рис. 6.1). Получится линия, называемая линией регрессии 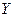 по
по 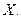


Рис. 6.1 Рис. 6.2
Однако по этим же точкам вы можете построить прямую линию, минимально отклоняющуюся от этих точек (рис. 6.2). Эта прямая называется прямой линией регрессии 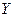 по
по 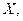 а её уравнение называется уравнением линейной регрессии
а её уравнение называется уравнением линейной регрессии 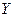 по
по 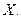
Уравнение линейной регрессии 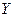 по
по 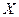 определяется формулой (31.2):
определяется формулой (31.2):

в которой в соответствии с (31.3)






О силе линейной связи между СВ 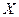 и
и 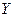 можно судить по коэффициенту корреляции
можно судить по коэффициенту корреляции

где
 ,
,  .
.
Чем ближе 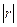 к
к  , тем сильнее связь между СВ
, тем сильнее связь между СВ 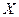 и
и 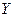 .
.
Коэффициент корреляции 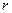 вычисляется по случайным значениям, поэтому
вычисляется по случайным значениям, поэтому 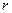 – случайное число. Следовательно, если
– случайное число. Следовательно, если  то это ещё не означает, что между СВ
то это ещё не означает, что между СВ 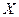 и
и 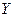 имеется линейная зависимость. Появляется необходимость проверить значимость (степень достоверности) числа
имеется линейная зависимость. Появляется необходимость проверить значимость (степень достоверности) числа  Для этого вычисляем
Для этого вычисляем

а также из таблицы распределения Стьюдента находим  . Наконец, выполняем проверку:
. Наконец, выполняем проверку:
Если   |
то коэффициент корреляции 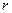 значим, т. е. с вероятностью значим, т. е. с вероятностью  можно признать, что между СВ можно признать, что между СВ 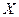 и и 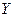 осуществляется линейная зависимость. осуществляется линейная зависимость. |
Вопросы к экзамену.
1. Задачи математической статистики. Основные понятия математической статистики.
2. Генеральная и выборочная совокупности. Виды выборок.
3. Статистическое распределение выборки. Эмпирическая функция распределения и её свойства.
4. Графики статистического распределения. Полигон и гистограмма частот и относительных частот.
5. Статистические оценки параметров распределения. Несмещённые, эффективные и состоятельные оценки.
6. Генеральная и выборочная средние.
7. Генеральная и выборочная дисперсии. Формула для вычисления дисперсии.
8. Числовые характеристики вариационного ряда.
9. Статистическая гипотеза.
10. Критерий согласия Пирсона.
