Тема: Определение работы газа.

Сначала определим, когда газ работает. Работа совершается, неважно, газом или еще кем (или чем), если что-то куда-то перемещено. Газ может переместить что-либо, только если изменит объем. Без изменения объема работа совершена быть не может. То есть, если в каком-то процессе объем не менялся, то и работы никакой нет. Определим элементарную работу газа 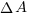, то есть о-очень маленькую. Пусть газ давит на некоторую пластину и перемещает ее на маленькое-маленькое расстояние 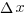, тогда работа газа 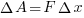. То есть газ должен давить на пластину с силой 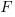. Эту силу определим как произведение давления газа на площадь пластины S: 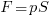. Как известно, газ одинаково давит во все стороны. То есть давление газа направлено нормально к нашей пластинке (перпендикулярно), направление действия силы совпадает с перемещением, угол, соответственно, равен 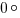, а его косинус равен 1. Так как перемещение у нас совсем маленькое, то считаем, что давление газа не изменилось. Запишем тогда, что у нас получается для работы: 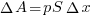. Если подумать, то произведение площади пластинки на малое перемещение ее 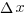– это ни что иное, как изменение объема сосуда. Тогда окончательно 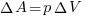. Не забываем, что мы нашли только очень маленькую часть работы (элементарную работу), чтобы найти полную работу, надо сложить маленькие-маленькие работки в одну макроработу (такую ощутимую уже работу :).

Для сложения тучи чего-то маленького в то, что можно пощупать или увидеть, существует интеграл:

.

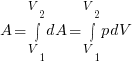Геометрический смысл определенного интеграла – это площадь криволинейной трапеции (площадь под кривой). Если объем газа в цикле сначала растет (работа положительна), а потом уменьшается (работа отрицательна), то в итоге газ совершает работу, которая пропорциональна площади фигуры, ограниченной линиями цикла (см. рисунок)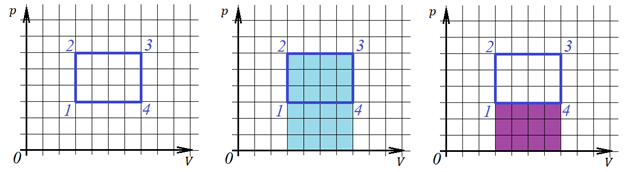

Здесь газ переходит сначала из состояния 1 в состояние 2, не совершая работы (изохорно), затем он переходит в состояние 3 изобарно, работа, которую он при этом совершает, равна площади голубого прямоугольника. Работа положительна, так как объем газа растет. Затем следует переход в точку 4, и снова работа газом не совершается. Из точки 4 газ возвращается в первоначальное состояние, работа, совершаемая им отрицательна (объем становится меньше, то есть газ сжимают внешние силы, работа которых как раз положительна). Отрицательная работа газа показана фиолетовым прямоугольником. Таким образом, вся работа, совершенная в этом цикле – это площадь прямоугольника 1-2-3-4.

Немного обобщим и подведем итог:

При изохорном процессе, так как объем не меняется, то работа равна нулю.

При изобарном процессе давление постоянно, вытащим его за знак интеграла:

.

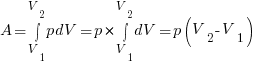А при изотермическом процессе происходит как изменение давления, так и объема. Выразим давление через объем с помощью уравнения Клапейрона -Менделеева:

:

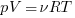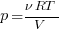
Подставим в наш интеграл:

.

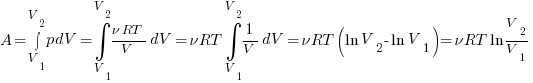Теперь порешаем различные задачи, чтобы изложенная теория прочно запомнилась.

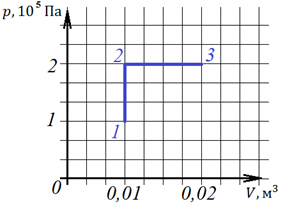
1.При переходе из состояния 1 в состояние 3 температура газа

1) увеличилась в 2 раза,

2) уменьшилась в 2 раза

3) увеличилась в 4 раза

4) уменьшилась в 4 раза.

С помощью уравнения Клапейрона -Менделеева: 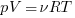заключаем, что температура газа прямо зависит от произведения его давления и объема. В состоянии 1 это произведение равно 0,01, а в состоянии 3 – 0,04, что больше в 4 раза, значит, и температура газа больше в 4 раза в третьем состоянии, чем в первом.

Ответ: 3

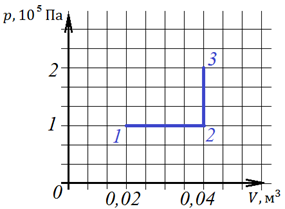
2.При переходе из состояния 1 в состояние 3 газ совершает работу

1) 2 кДж

2) 4 кДж

3) 6 кДж

4) 8 кДж

На рисунке процесс 1-2 – изобарный, выше мы записали, как рассчитать работу газа в таком процессе:

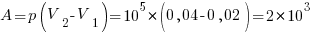Дж, или 2 кДж.

Из состояния 2 в состояние 3 газ переходит изохорно, его объем не меняется, поэтому работа не совершается.

Ответ: 1.

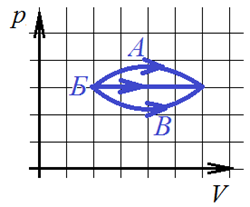
3.В каком из процессов перехода идеального газа из состояния 1 в состояние 2 газ совершает наибольшую работу?

1) А

2) Б

3) В

4) Во всех трех процессах совершаемая работа одинакова

Вспоминаем, что работа газа в осях p-V есть интеграл, а интеграл – это площадь криволинейной трапеции. Площадь такой трапеции максимальна при переходе газа из начального состояния в конечное по траектории А.

Ответ: 1.

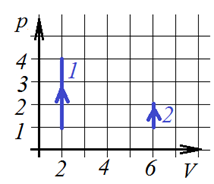
4.В двух сосудах находится одинаковое количество азота. С газами в сосудах происходят процессы, показанные на pV-диаграммах 1 и 2. Сравните работы, совершенные над газами в сосудах.

1)

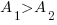
2)

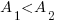
3)

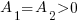
4)

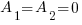
Так как ни в первом, ни во втором случае объем газа не меняется (тип газа нам тоже не важен), то работы никакой газы не совершают.

Ответ:4.

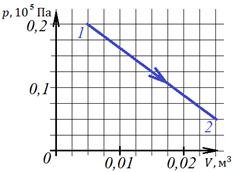
5.Какую работу совершил одноатомный газ в процессе, изображенном на диаграмме?

1) 250 Дж

2) 150 Дж

3) 300 Дж

4) 400 Дж

Решить задачу можно, определив площадь трапеции по формуле: 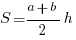. При этом за основания трапеции примем величины давлений в состояниях 1 и 2, а высота – изменение объема. Тогда:

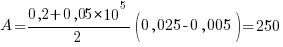
Ответ: 1.