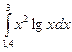Порядок выполнения заданий
Тогда при таком допущении из (3.7) следует
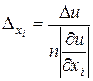 .
. 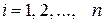 (3.9)
(3.9)
Отметим, что влияние ошибок измерений на результат в некоторых ситуациях целесообразнее изучать методами математической статистики.
Следует иметь в виду, что в полевых данных особо тщательно должны анализироваться систематические погрешности, здесь имеются в виду случаи, когда все измерения или только меньше, или только больше соответствующего точного числа. Это обстоятельство может быть обусловлено, в частности, особенностями методики измерения.
Для наглядности рассмотрим оценку пористости газо-, водо- и керосинонасыщением для различных типов пород. Метод газонасыщения по своей физической основе точнее методов насыщения жидкостью, так как газ, имея меньший размер молекул и меньшую вязкость по сравнению с жидкостью, может пройти в самые тонкие поры горной породы. То же самое можно сказать про водо- и керосинонасыщение. Вода более активная в связи с её полярностью и меньшим размером молекул. Отсюда следует, что пористость, установленная по газо- или водонасыщению в отдельных случаях может оказаться выше пористости, определенной по насыщению керосином. Это особенно актуально для крепко сцементированных песчано-алевролитовых и алевролитовых пород с большим количеством цемента, характеризующихся наличием тонких пор. При измерении открытой пористости таких пород метод керосинонасыщения даёт систематическую ошибку, величина которой колеблется от 2% до 7-9%.
Варианты заданий
№ 1 № 2
1)  =6,63; 19/41=0,463. 1)7/15=0,467;
=6,63; 19/41=0,463. 1)7/15=0,467; 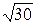 =5,48.
=5,48.
2) а) 22,553 (±0,016); 2) а) 17,2834; d=0,3%;
б) 2,8546; d=0,3%. б) 6,4257 (±0,0024).
3) х=37,1 Dх=0,3 3) х=12,7 Dх=0,1
у=9,87 Dу=0,11 у=8,1 Dу=0,09 
z=6,052 Dz=0,016. z=4,7 Dz=0,071.
4) х1=2,10415 4) х1=3,10815
x2=1,93521 x2=1,17516
х3=0,84542. х3=0,75112.
№ 3 № 4
1) 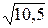 =3,24; 4/17=0,235. 1)15/7=2,14;
=3,24; 4/17=0,235. 1)15/7=2,14; 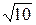 =3,16.
=3,16.
2) а) 34,834; d=0,1% 2) а) 2,3485 (±0,0042);
б) 0,5748 (±0,0034). б) 0,34484; d=0,4%.
3) х=47,6 Dх=0,41 3) х=48,3 Dх=0,39
у=6,81 Dу=0,12 у=7,53 Dу=0,15 
z=3,971 Dz=0,014. z=1,786 Dz=0,016.
4) х1=7,85169 4) х1=9,15176
x2=1,17972 x2=1,18186
х3=0,75413. х3=0,85176.
№ 5 № 6
1) 6/7=0,857; 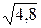 =2,19. 1)12/11=1,091;
=2,19. 1)12/11=1,091; 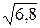 =2,61.
=2,61.
2) а) 5,435 (±0,0028); 2) а) 8,24163; d=0,2%;
б) 10,8441; d=0,5%. б) 0,12356 (±0,00036).
3) х=67,4 Dх=0,28 3) х=46,7 Dх=0,33
у=4,57 Dу=0,14 у=5,47 Dу=0,15 
z=1,814 Dz=0,013. z=1,711 Dz=0,012.
4) х1=6,18174 4) х1=9,17514
x2=1,17564 x2=1,74116
х3=0,97415. х3=0,87445.
№ 7 № 8
1) 2/21=0,095; 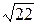 =4,69. 1)23/15=1,53;
=4,69. 1)23/15=1,53; 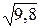 =3,13.
=3,13.
2) а) 2,4543 (±0,0032); 2) а) 23,574; d=0,2%;
б) 24,5643; d=0,1%. б) 8,3445 (±0,0022).
3) х=27,5 Dх=0,14 3) х=39,4 Dх=0,31
у=8,15 Dу=0,11 у=6,54 Dу=0,13 
z=2,817 Dz=0,009. z=2,154 Dz=0,011.
4) х1=8,12514 4) х1=7,16417
x2=1,85412 x2=1,75344
х3=0,75416. х3=0,91415.
№ 9 № 10
1)6/11=0,545; 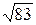 =9,11. 1)17/19=0,889;
=9,11. 1)17/19=0,889; 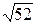 =7,21.
=7,21.
2) а) 21,68563; d=0,3% 2) а) 13,537 (±0,0026);
б) 3,7834 (±0,0041). б) 7,521; d=0,12%.
3) х=44,5 Dх=0,29 3) х=48,3 Dх=0,29
у=8,15 Dу=0,14 у=5,71 Dу=0,15 
z=1,759 Dz=0,09. z=1,684 Dz=0,011.
4) х1=8,16744 4) х1=9,17127
x2=1,81234 x2=1,94564
х3=0,81514. х3=0,81576.
№ 11 № 12
1)21/29=0,723; 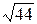 =6,63. 1)50/19=2,63;
=6,63. 1)50/19=2,63; 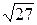 =5,19.
=5,19.
2) а) 0,3567; d=0,042% 2) а) 1,784 (±0,0063);
б) 13,6253 (±0,0021). б) 0,85637; d=0,21%.
3) х=54,7 Dх=0,28 3) х=49,4 Dх=0,24
у=6,44 Dу=0,11 у=6,71 Dу=0,12 
z=1,781 Dz=0,012. z=1,814 Dz=0,09.
4) х1=8,17564 4) х1=9,75413
x2=2,81344 x2=4,75641
х3=0,81425. х3=1,12834.
№ 13 № 14
1) 13/17=0,764; 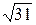 =5,56. 1)7/22=0,318;
=5,56. 1)7/22=0,318; 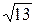 =3,60.
=3,60.
2) а) 3,6878 (±0,0013); 2) а) 27,1548 (±0,0016);
б) 15,873; d=0,42%. б) 0,3945; d=0,16%.
3) х=64,7 Dх=0,31 3) х=81,2 Dх=0,27
у=7,56 Dу=0,17 у=6,14 Dу=0,30 
z=1,749 Dz=0,09. z=1,471 Dz=0,12.
4) х1=8,94567 4) х1=8,17453
x2=6,17581 x2=0,94155
х3=1,13447. х3=6,17441.
№ 15 № 16
1) 17/11=1,545; 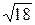 =4,243. 1)5/3=1,667;
=4,243. 1)5/3=1,667; 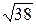 =6,16.
=6,16.
2) а) 0,8647 (±0,0013); 2) а) 3,7542; d=0,32%;
б) 24,3618; d=0,22%. б) 0,98351 (±0,00042).
3) х=74,9 Dх=0,29 3) х=84,6 Dх=0,28
у=7,15 Dу=0,22 у=6,48 Dу=0,19 
z=1,916 Dz=0,11. z=1,864 Dz=0,09.
4) х1=9,53475 4) х1=9,75481
x2=6,18445 x2=5,17841
х3=1,12417. х3=1,28412.
№ 17 № 18
1)49/13=3,77; 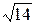 =3,74. 1)13/7=1,857;
=3,74. 1)13/7=1,857; 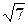 =2,64.
=2,64.
2) а) 83,736; d=0,085% 2) а) 2,8867; d=0,43%;
б) 5,6483 (±0,0017). б) 32,7486 (±0,0012).
3) х=84,7 Dх=0,31 3) х=84,7 Dх=0,28
у=5,47 Dу=0,21 у=6,47 Dу=0,15 
z=2,754 Dz=0,13. z=1,754 Dz=0,09.
4) х1=8,17564 4) х1=7,94754
x2=5,41746 x2=6,53427
х3=2,11456. х3=1,12147.
№ 19 № 20
1) 19/12=1,58; 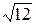 =3,46. 1)51/11=4,64;
=3,46. 1)51/11=4,64; 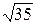 =5,91.
=5,91.
2) а) 4,88445 (±0,00052); 2) а) 38,4258 (±0,0014);
б) 0,096835; d=0,32%. б) 0,66385; d=0,34%.
3) х=16,4 Dх=0,21 3) х=45,7 Dх=0,29
у=7,15 Dу=0,16 у=7,17 Dу=0,15 
z=2,127 Dz=0,09. z=1,214 Dz=0,12.
4) х1=7,12415 4) х1=7,15427
x2=8,75112 x2=3,74184
х3=0,75927. х3=0,84415.
№ 21 № 22
1) 18/7=2,57; 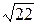 =4,69. 1)17/9=2,11;
=4,69. 1)17/9=2,11; 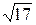 =4,12.
=4,12.
2) а) 0,39642 (±0,00022); 2) а) 5,8425; d=0,23%;
б) 46,453; d=0,15%. б) 0,66385 (±0,00042).
3) х=83,7 Dх=0,31 3) х=87,5 Dх=0,30
у=6,54 Dу=0,21 у=11,54 Dу=0,15 
z=1,182 Dz=0,11. z=1,768 Dz=0,09.
4) х1=8,56423 4) х1=8,76465
x2=6,75447 x2=6,74275
х3=0,98476. х3=0,95443.
№ 23 № 24
1)16/7=2,28; 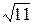 =3,32. 1)21/13=1,54;
=3,32. 1)21/13=1,54; 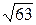 =7,94.
=7,94.
2) а) 24,3872; d=0,34% 2) а) 2,3684 (±0,0017);
б) 0,75244 (±0,00013). б) 45,7832; d=0,18%.
3) х=64,5 Dх=0,29 3) х=79,9 Dх=0,29
у=11,71 Dу=0,17 у=9,75 Dу=0,17 
z=1,841 Dz=0,08. z=1,165 Dz=0,09.
4) х1=9,17156 4) х1=8,17644
x2=0,75441 x2=0,19561
х3=7,14556. х3=9,17441.
№ 25 № 26
1)12/7=1,71; 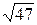 =6,86. 1)6/7=0,857;
=6,86. 1)6/7=0,857; 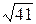 =6,40.
=6,40.
2) а) 72,354; d=0,24% 2) а) 0,36127 (±0,00034);
б) 0,38725 (±0,00112). б) 46,7843; d=0,32%.
3) х=84,5 Dх=0,32 3) х=75,9 Dх=0,34
у=8,94 Dу=0,21 у=6,12 Dу=0,17 
z=1,754 Dz=0,08. z=0,975 Dz=0,07.
4) х1=7,18171 4) х1=8,15141
x2=2,24157 x2=3,27154
х3=0,75416. х3=0,84114.
№ 27 № 28
1)23/9=2,56; 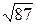 =9,33. 1)27/31=0,872;
=9,33. 1)27/31=0,872; 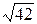 =6,48.
=6,48.
2) а) 23,7564; d=0,44% 2) а) 15,8372 (±0,0026);
б) 4,57633 (±0,00042). б) 0,088748; d=0,56%.
3) х=91,7 Dх=0,39 3) х=92,9 Dх=0,42
у=8,14 Dу=0,18 у=11,44 Dу=0,21 
z=1,124 Dz=0,06. z=1,711 Dz=0,08.
4) х1=9,97115 4) х1=8,25661
x2=2,84114 x2=3,70415
х3=0,79405. х3=1,81615.
№ 29 № 30
1)7/3=2,33; 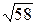 =7,61. 1)14/17=0,823;
=7,61. 1)14/17=0,823; 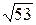 =7,28.
=7,28.
2) а) 3,87683; d=0,33% 2) а) 0,66835 (±0,00115);
б) 13,5726 (±0,0072). б) 23,3748; d=0,27%.
3) х=54,2 Dх=0,23 3) х=79,9 Dх=0,37
у=12,11 Dу=0,17 у=24,15 Dу=0,19 
z=2,124 Dz=0,10. z=1,184 Dz=0,12.
4) х1=7,12415 4) х1=9,87154
x2=4,90415 x2=3,91164
х3=0,12715. х3=1,17156
Функции к вариантам третьих заданий
№ 1-2 u = x×y2×z3
№ 3-4 u = x3×y2×z
№ 5-6 u = x×y3×z2
№ 7-8 u = x2×y×z3
№ 9-10 u = x3×y2×z
№ 11-12 u = x3×y×z2
№ 13-14 u = x2×y3×z
№ 15-16 u = x2×y2×z3
№ 17-18 u = x2×y2×z2
№ 19-20 u = x3×y2×z2
№ 21-22 u = x2×y3×z2
№ 23-24 u = x2×y3×z3
№ 25-26 u = x×y4×z2
№ 27-28 u = x4×y×z
№ 29-30 u = x×y4×z
3.4. Порядок выполнения заданий
1. Определить: какое из двух равенств точнее.
За точные числа взять значения данных выражений с большим числом десятичных знаков (на три). После определения погрешности каждого выражения, написать вывод с его обоснованием.
2. Найти интервалы точного числа двумя способами:
а) через абсолютную погрешность;
б) через относительную погрешность.
Округлить числа, оставив только верные знаки. Определить предельную абсолютную и предельную относительную погрешности полученных приближенных чисел.
3. Вычислить значение функции u и предельную абсолютную и относительную ошибки функции u для данных значений х, у, z и абсолютных погрешностей аргументов. Значение 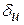 найти двумя способами:
найти двумя способами:
а) по формуле относительной погрешности непрерывной дифференцируемой функции. Для этого необходимо вначале получить формулу относительной погрешности для предложенной функции, исходя из оценки погрешности непрерывной дифференцируемой функции в общем виде (3.8);
б) по определению относительной погрешности,
г) сравнить относительные погрешности, найденные разными способами и по результатам сравнения написать вывод.
4. Найти допустимые абсолютные погрешности аргументов, которые позволяют вычислить значение данной функции u = х1×х2 + х2×х3 + х1×х3 с четырьмя верными знаками после запятой.
Для этого предварительно вывести формулы абсолютных погрешностей аргументов заданной функции, исходя из решения обратной задачи теории погрешностей в общем виде (3.9).
3.5. Решение одного варианта
1) 9/11=0,818; 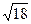 =4,24;
=4,24;
2) а) 72,353( 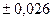 ); б) 2,3544;
); б) 2,3544; 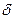 =0,2%;
=0,2%;
3) а) 0,4357; б) 12,384.
1) Находим значения данных выражений с большим числом десятичных знаков: 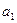 =9/11=0,81818…,
=9/11=0,81818…, 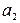 =
= 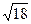 =4,2426. Затем вычисляем предельные абсолютные погрешности:
=4,2426. Затем вычисляем предельные абсолютные погрешности:
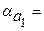
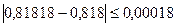 ,
, 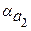 =
= 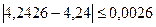 .
.
Предельные относительные погрешности составляют
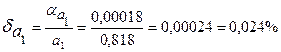 ,
,
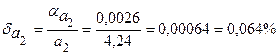 .
.
Вывод. Так как 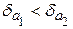 , то равенство 9/11=0,818 является более точным.
, то равенство 9/11=0,818 является более точным.
2) а) Пусть 72,353(  0,026). Согласно условию, предельная абсолютная
0,026). Согласно условию, предельная абсолютная  погрешность
погрешность 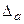 =0,026, значит, число верных знаков m=3, а=72.4 (т.е. в числе 72,353 верными являются цифры 7, 2, 3). Предельная абсолютная погрешность полученного приближения
=0,026, значит, число верных знаков m=3, а=72.4 (т.е. в числе 72,353 верными являются цифры 7, 2, 3). Предельная абсолютная погрешность полученного приближения 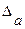 =0,026+0,047=0,073. Предельная относительная погрешность приближения а
=0,026+0,047=0,073. Предельная относительная погрешность приближения а 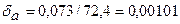 . Интервалы точного числа через предельную абсолютную погрешность (3.3):
. Интервалы точного числа через предельную абсолютную погрешность (3.3):
72,4-0,073 £ А £ 72,4+0,073
72,327£ А £ 72,473,
через предельную относительную погрешность (3.4):
72,4(1-0,00101) £ А £ 72,4(1+0,00101)
72,327£ А £ 72,473.
Вывод. В обоих случаях получили один и тот же интервал. Это говорит о правильности расчётов.
б) а=2,3544; 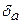 =0,2%=0,002;
=0,2%=0,002; 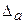 =
= 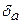 ×а=0,00471.
×а=0,00471.
Далее аналогично вычислениям в предыдущем пункте.
3) а) u=x×y2×z3, х = 1,2; у = 2,1; z = 1,6; Dх = 0,17; Dу = 0,05; Dz=0,02.
u (1,2; 2,1; 0,6)= 21,67603.
Формула (3.7) для рассматриваемой функции имеет вид:
Du=y2×z3Dх+2×х×у×z3×Dу+3×х×у2×z2×Dz.
Для заданных значений Du=4,915814.
Исходя их формулы (3.8), получим выражение для относительной погрешности:
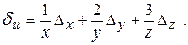
Отсюда, 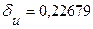 .
.
б) 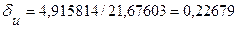 .
.
Вывод. Относительные погрешности, найденные разными способами совпадают, что подтверждает правильность полученной формулы.
4) Для функции u=x2+y2+z3 выражения допустимых абсолютных погрешностей аргументов (3.9) имеют вид:
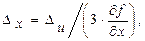
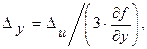
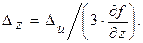
Пусть х=12,14; у=7,89; z=2,17; Du=0,00005 (по условию задачи на стр. 8). Тогда Dх=0,0000041; Dу=0,0000063; Dz=0,000023.
4. ЛИНЕЙНАЯ АЛГЕБРА
4.1. Цель работы
Овладеть точными и приближёнными методами решения систем линейных алгебраических уравнений, научиться находить оценку точности найденного решения и определять пороговые значения, позволяющие остановить итерационный процесс после нахождения решения с заданной точностью.
4.1. Методические указания
Методы решения систем линейных алгебраических уравнений (СЛАУ) делятся на две группы:
1) точные методы, представляющие собой конечные алгоритмы нахождения корней системы (таковы, например, метод Гаусса, правило Крамера, метод Халецкого и др.);
2) итерационные методы, позволяющие получать корни системы с заданной точностью путем построения конечной, а чаще бесконечной последовательности приближений, итераций (к их числу относятся метод простых итераций, метод Зейделя, метод релаксаций и др.).
4.1.1. Метод простых итераций. Рассмотрим систему линейных уравнений вида
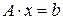 , (4.1)
, (4.1)
где 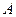 - квадратная матрица, причем
- квадратная матрица, причем 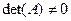 ,
, 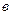 и
и 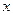 - n-мерные вектора,
- n-мерные вектора, 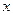 - неизвестный (искомый) вектор.
- неизвестный (искомый) вектор.
Приведем систему (4.1) к виду
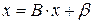 , (4.2)
, (4.2)
где 
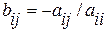 ,
, 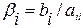 .
.
Метод простых итераций состоит в следующем. Выбирается произвольный вектор 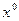 (начальное приближение) и строится итерационная последовательность векторов по формуле
(начальное приближение) и строится итерационная последовательность векторов по формуле
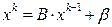 ,
, 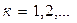 (4.3)
(4.3)
Теорема 1. Если 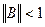 , то система линейных уравнений (4.2) имеет единственное решение
, то система линейных уравнений (4.2) имеет единственное решение 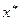 и итерации (последовательные приближения) (4.3) сходятся к решению со скоростью геометрической прогрессии.
и итерации (последовательные приближения) (4.3) сходятся к решению со скоростью геометрической прогрессии.
Через 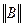 здесь обозначена норма матриц вида:
здесь обозначена норма матриц вида:
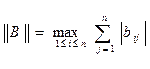 . (4.4)
. (4.4)
Для оценки точности приближения 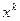 , полученного на к-ой итерации по формуле (4.3), используется неравенство
, полученного на к-ой итерации по формуле (4.3), используется неравенство
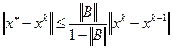 . (4.5)
. (4.5)
Через 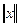 в (4.5) обозначена норма вектора вида.
в (4.5) обозначена норма вектора вида.
С точки зрения теории погрешностей левая часть (4.5) есть абсолютная погрешность приближения 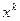 СЛАУ (4.2). Неравенство (4.5) можно использовать для нахождения предельной абсолютной погрешности приближения
СЛАУ (4.2). Неравенство (4.5) можно использовать для нахождения предельной абсолютной погрешности приближения 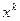 , на основе правой части формулы (4.5).
, на основе правой части формулы (4.5).
Из формулы (4.5) можно найти величину, позволяющую останавливать итерационный процесс (4.3) в автоматическом режиме, если задана точность 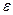 , с которой требуется найти приближенное решение. Действительно,
, с которой требуется найти приближенное решение. Действительно, 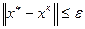 , а величина
, а величина 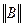 определяется по формуле (4.4). Для рассматриваемой ситуации из (4.5) получаем
определяется по формуле (4.4). Для рассматриваемой ситуации из (4.5) получаем 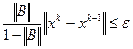 . Из этого неравенства следует
. Из этого неравенства следует
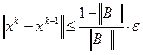 . (4.6)
. (4.6)
Неравенство (4.6) должно проверяться на каждой итерации. Как только оно будет выполнено, итерационный процесс должен быть остановлен, так как требуемая точность достигнута.
4.1.2. Метод Зейделя. Рассмотрим СЛАУ (4.2). Метод Зейделя состоит в том, что итерации производятся по формуле
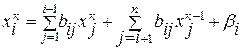 , (4.7)
, (4.7)
где 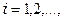
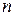 ,
, 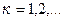
Итерации (4.7) по методу Зейделя отличаются от простых итераций (4.2) тем, что при нахождении 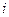 - ой компоненты
- ой компоненты 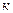 - го приближения используются уже найденные компоненты
- го приближения используются уже найденные компоненты 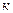 - го приближения, а именно, 1,2,…,
- го приближения, а именно, 1,2,…, 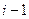 компоненты.
компоненты.
Теорема 2. Если линейная система (4.1) нормальная (симметричная и положительно определенная), то процесс Зейделя для эквивалентной ей приведенной системы (4.2) всегда сходится из любого начального вектора 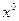 .
.
Способ приведения линейной системы (4.1) к нормальному виду следует из теоремы.
Теорема 3. Если обе части линейной системы (4.1) умножить слева на транспонированную матрицу 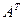 , то полученная новая система линейных уравнений
, то полученная новая система линейных уравнений 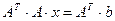 будет нормальной.
будет нормальной.
Оценка погрешности для метода Зейделя имеет вид
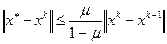 , (4.8)
, (4.8)
где 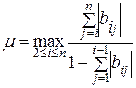 .
.
4.1.3. Метод Халецкого. Этот метод (точный) основан на том, что почти всякую квадратную матрицу 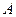 можно представить в виде произведения нижней треугольной
можно представить в виде произведения нижней треугольной 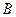 и верхней треугольной
и верхней треугольной 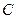 с единичной диагональю, т.е. в виде
с единичной диагональю, т.е. в виде 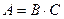 . Так как матрицы
. Так как матрицы 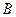 и
и 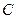 треугольные, то их элементы выражаются аналитически
треугольные, то их элементы выражаются аналитически
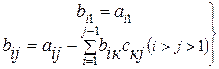 (4.9)
(4.9)
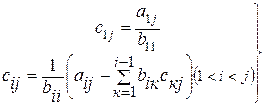 . (4.10)
. (4.10)
После нахождения матриц 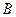 и
и 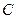 искомый вектор
искомый вектор 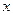 может быть вычислен из двух систем уравнений:
может быть вычислен из двух систем уравнений:
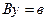 ,
, 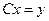 . (4.11)
. (4.11)
В силу треугольности матриц 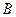 и
и 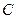 , система (4.10) решается в явном виде:
, система (4.10) решается в явном виде:
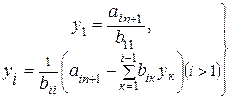 (4.12)
(4.12)
и 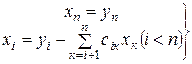 . (4.13)
. (4.13)
Этот метод получил название схемы Халецкого. В схеме применяется обычный контроль с помощью сумм. Над столбцом сумм производим те же действия, что и над столбцом свободных членов.
4.1.4. Нахождение обратной матрицы методом Халецкого. Обратной матрицей А-1 по отношению к данной А называется матрица, которая при умножении как справа, так и слева на данную матрицу А, дает единичную матрицу:
А-1×А=А×А-1=Е, (4.14)
где Е - единичная матрица.
Квадратная матрица называется неособенной, если ее определитель отличен от нуля:
det(А)¹0. … (4.15)
Теорема 4. Всякая неособенная матрица имеет единственную обратную матрицу.
Рассмотрим вычисление обратной матрицы методом Халецкого. Из равенства А=В×С следует
А-1=С-1×В-1 (4.16)
Умножая (4.16) вначале слева на С, затем справа на В, получим равенства:
А-1×В=С-1 (4.17)
С×А-1=В-1. (4.18)
Обозначим элементы матрицы А-1 через dij, т.к. С-1 – верхняя треугольная, причем сii=1, i=1, 2,…, n, то (4.17) представляет систему 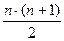 уравнений для определения dij:
уравнений для определения dij:
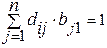 0 0…0
0 0…0
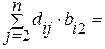 1 0…0 (4.19)
1 0…0 (4.19)
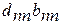 = 1
= 1
i=1, 2,…, n.
Так как В-1 – нижняя треугольная матрица, то (4.18) представляет систему 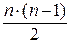 уравнений:
уравнений:
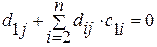 0 0…0
0 0…0
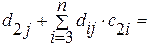 0 0…0 (4.20)
0 0…0 (4.20)
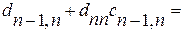 0
0
j=2, 3,…, n.
Итак, (4.19) и (4.20) является системой n2 линейных уравнений для вычисления n2 элементов А-1. Решение этой системы не содержит принципиальных трудностей. На первом шаге в каждом из уравнений (4.19) полагаем i=n и находим последовательно dnn, dn, n-1, dn1. На втором шаге из (4.20) при j=n вычисляем dn-1, n, dn-2, n,…, d1n. Затем при i=n-1 из (4.19) находим dn-1, n-1, dn-1,n-2,…, dn-1, 1 и т. д.
4.1.5. Собственные векторы и собственные значения матриц. Рассмотрим квадратную матрицу А=[aij], i,j=1, 2,…, n и n-мерный вектор х¹0.
Вектор х¹0 называется собственным вектором матрицы А, если найдется число l такое, что имеет место равенство:
А×х=l×х. (4.21)
Число l в (4.21) называется собственным значением или характеристическим числом матрицы А, соответствующим собственному вектору х.
Рассмотрим алгоритм нахождения собственных элементов нормальной (симметричной и положительно определенной) матрицы.
Если матрица нормальная, то ее собственные элементы обладают двумя важными свойствами:
1. Собственные числа l1, l2,…, ln её действительны и положительны;
2. Собственные векторы хi, i=1, 2,…, n действительны и взаимно ортогональны:
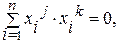 при j¹к.
при j¹к.
Исходя из теоремы существования, первый собственный вектор х1 и l1 определяются из системы линейных уравнений:
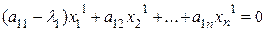
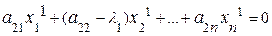
. . . . . . .
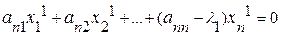
Приведем эту систему к виду, необходимому для итерационного процесса:
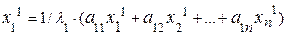
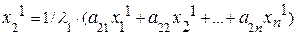
. . . . . . . (4.22)
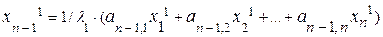
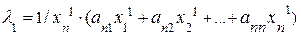 .
.
Так как координаты собственных векторов определяются с точностью до множителя пропорциональности, то одна из них произвольная, для определенности возьмем 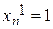 . Систему (4.21) можно решать и методом итераций, и методом Зейделя.
. Систему (4.21) можно решать и методом итераций, и методом Зейделя.
Для определения l2 и х2 СЛАУ имеет вид:
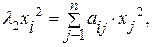 i=1, 2,…, n.
i=1, 2,…, n.
Из соотношения ортогональных векторов х1 и х2:
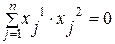
исключим одну из компонент вектора х2, например, хn2. Тогда система для определения l2 и х2 примет вид:
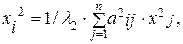 i=1, 2,…, n-2
i=1, 2,…, n-2
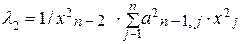 . (4.23)
. (4.23)
Полагая 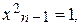 решим системы (4.23) и тем самым найдем l2 и х2.
решим системы (4.23) и тем самым найдем l2 и х2.
Порядок выполнения заданий
Задание 1. Решение системы линейных уравнений методом простых итераций.
1. Привести полный текст варианта.
2. Преобразовать систему линейных уравнений к виду, необходимому для метода простых итераций.
3. Проверить условие сходимости метода простых итераций.
4. Определить, какова должна быть норма разности векторов на двух соседних итерациях 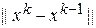 , гарантирующая получение решения с заданной точностью
, гарантирующая получение решения с заданной точностью 
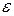 =0,005.
=0,005.
5. Решить систему методом простых итераций c точностью 
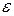 =0,005, используя результаты предыдущего пункта для остановки итерационного процесса.
=0,005, используя результаты предыдущего пункта для остановки итерационного процесса.
6. Написать интервалы для точного решения системы линейных уравнений.
Задание 2. Решение системы линейных уравнений методом Зейделя.
1. Преобразовать систему линейных уравнений к эквивалентному нормальному виду для решения ее методом Зейделя.
2. Решить преобразованную систему методом Зейделя, сделав 5 итераций.
3. Найти предельную абсолютную погрешность приближения, найденного на пятой итерации.
4. Написать интервалы точного решения системы линейных уравнений.
Задание 3. Решить системы линейных уравнений методом Халецкого.
1. Найти треугольные матрицы В и С, удовлетворяющие условию: 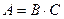 .
.
2. Определить вектор 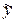 и вектор
и вектор 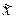 .
.
3. Сравнить точность вектора 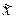 и приближений, найденных методами простых итераций и Зейделя. Оценить погрешность решения, найденного методом Халецкого, взяв за точное решение приближение, найденное методом простых итераций.
и приближений, найденных методами простых итераций и Зейделя. Оценить погрешность решения, найденного методом Халецкого, взяв за точное решение приближение, найденное методом простых итераций.
4. Уточнить решение 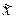 , если его абсолютная погрешность превышает 0,05.
, если его абсолютная погрешность превышает 0,05.
Задание 4. (Самостоятельная работа) Нахождение обратной матрицы методом Халецкого.
1. Найти обратную матрицу А-1, используя матрицы В и С, вычисленные в задании 3.
2. Сделать проверку правильности вычисления А-1, используя определение обратной матрицы.
Задание 5. (Самостоятельная работа) Собственные вектора и собственные числа квадратных нормальных матриц.
1. Найти одно собственное число и соответствующий собственный вектор для нормальной матрицы, вычисленной в задании 2.
2. Сделать проверку правильности вычислений, на основе определения собственных чисел и собственных векторов.
3. Составить систему линейных уравнений для нахождения второго собственного числа и соответствующего собственного вектора. При составлении системы учесть свойство ортогональности собственных векторов нормальных матриц.
Варианты заданий
| № 1 10х1+2х2 +2х3 +2х4=16 -х1+10х2- х3 - х4=7 -2х1 - х2 +10х3+2х4=9 -х1 - х2 - 2х3 + 10х4=6 | № 2 10х1+ х2+ х3 + х4=13 х1+10х2 - х3 - х4=9 х1+ 2х2+10х3+ х4=14 -х1 - х2- х3+ 10х4=7 | ||||||
| № 3 10х1+2х2+ х3 +2х4=15 2х1+10х2+2х3+2х4=16 х1+х2+10х3+2х4=14 -х1-х2- х3+10х4=7 | № 4 10х1+2х2+2х3+ х4=15 х1+10х2+2х3 - 2х4=11 2х1+2х2+10х3 - 2х4=12 -2х1 - 2х2+2х3+10х4=8 | ||||||
| № 5 10х1+х2+2 х3+ х4=14 -х1+10х2- х3- 2х4=6 2х1+2х2 +10х3+ х4=15 -х1+х2+2х3+10 х4=12 | № 6 10х1+х2+ х3+ х4=13 х1+10х2+2х3-2х4=11 -х1+х2+10х3+2х4=12 -х1-2х2- 2х3+10х4=5 | ||||||
| № 7 10х1+2х2+ х3- х4=12 -х1+10х2- х3-2х4=6 -х1-2х2+ 10х3+ х4=8 -2х1+2х2+ 2х3+ 10х4=12 | № 8 10х1+х2+ х3+ 2х4=14 -х1+10х2- х3 -2 х4=6 2х1+2х2+ 10х3+ х4=15 -х1-2х2+х3+10х4=8 | ||||||
| № 9 10х1+2х2+3х3+3х4=18 -х1+10х2+ 2х3+2х4=13 -2х1-2х2+10х3- 2х4=4 2х1+х2+х3+10х4=14 | № 10 10х1+х2+2х3+ 2х4=15 -х1+10х2-х3- 2х4=6 2х1+2х2+10х3+ 2х4=16 -х1-х2-х3+ 10х4=7 | ||||||
| № 11 10х1+х2+2х3+ 2х4=15 х1+10х2+х3+ х4=13 -х1-х2+10х3+ 2х4=10 -х1-х2+х3+10 х4=9 | № 12 10х1+2х2+х3+ х4=14 х1+10х2-2х3- 2х4=7 2х1+2х2+10х3+ 2х4=16 -х1-х2+2х3+ 10х4=10 | ||||||
| № 13 10х1+2х2+2х3+ 2х4=16 х1+10х2-2х3-2 х4=7 2х1+3х2+10х3+ 2х4=17 -2х1-2х2-2х3+ 10х4=4 | № 14 10х1+х2+2х3+ х4=14 х1+10х2+х3- х4=11 х1+х2+10х3+ 3х4=15 -х1-х2-х3+ 10х4=7 | ||||||
| № 15 10х1+х2+х3+ х4=13 х1+10х2 - х3 - х4=9 -х1 - х2+10х3 - х4=7 2х1+2х2+х3+ 10х4=15 | № 16 10х1+х2+х3+ х4=13 2х1+10х2+2х3+ х4=15 -х1-х2+10х3- х4=7 -2х1-2х2+х3+ 10х4=7 | ||||||
| № 17 10х1+х2+х3+ 2х4=14 х1+10х2-х3- х4=9 х1+х2+10х3+ х4=13 х1-х2-2х3+ 10х4=8 | № 18 10х1+х2+х3+ х4=13 х1+10х2+2х3- х4=12 -х1-х2+10х3+ х4=9 х1-2х2+2х3+ 10х4=11 | ||||||
| № 19 10х1+х2 + 2х3+ 3х4=16 х1+10х2-2х3- 2х4 =7 -х1-2х2+10х3-2х4=5 2х1+3х2+2х3+ 10х4=17 | № 20 10х1+3х2 + 2х3+ 3х4=18 -х1+10х2 - 2х3 - 2х4=5 х1+х2 + 10х3+ х4=13 2х1-2х2 + х3+ 10х4=11 | ||||||
| № 21 10х1+х2 + 2х3+ х4=14 х1+10х2 - х3 - х4=11 х1+2х2 + 10х3- 3х4=10 х1+х2 + х3+ 10х4=13 | № 22 10х1+х2 - 2х3- 2х4=7 х1+10х2 + х3 - 4х4=8 х1+2х2 + 10х3 - 3х4=10 х1 + х2 + 2х3+ 10х4=14 | ||||||
| № 23 10х1+2х2 - 2х3 - х4=9 -х1+10х2 - 2х3- 2х4=5 х1+х2 + 10х3+ х4=13 -х1- х2 + 2х3+ 10х4=10 | № 24 10х1- х2 - 2х3-2х4=5 2х1+10х2 + х3+ 2х4=15 -х1- х2 + 10х3-2х4=6 -2х1-2х2 - 2х3+10х4=4 | ||||||
| № 25 10х1+х2 - 2х3 - 2х4=7 -х1+10х2 + х3 - 2х4=8 х1-2х2 +10х3+2х4=11 2х1+2х2 + 2х3+ 10х4=16 | № 26 10х1-х2 - х3 - 2х4=6 х1+10х2 - 2х3 - 2х4=7 х1+х2 + 10х3- 2х4=10 х1+х2 + х3+ 10х4=13 | ||||||
| №27 10х1+х2 + 2х3 + 2х4=15 -х1+10х2 + 2х3 + 2х4=13 -х1- 2х2 + 10х3 - 2х4=5 2х1+2х2 + 3х3+10х4=17 | №28 10х1+2х2 + х3 + х4=14 -2х1+10х2 +3х3 + 3х4=14 х1+х2 +10х3 + х4=13 -х1- х2 + х3 + 10х4=9 | ||||||
| № 29 10х1+х2 + 2х3 + 2х4=15 х1+10х2 + 3х3 + х4=15 2х1+2х2 + 10х3 + 2х4=16 х1+х2 + х3 + 10х4=13 | №30 10х1+х2 - х3 - х4=9 х1+10х2 - 3х3 + 2х4=10 -х1+2х2 +10х3 - 2х4=9 х1+2х2 + 2х3 + 10х4=15 | ||||||
4.4. Решение одного варианта
4.4.1. Решить систему линейных уравнений
10х1+2х2+х3=13
х1+10х2+х3=12 (4.24)
-х1-х2+10х3=8
с точностью ε=0,001.
Преобразуем систему (4.24) к виду:
х1=1,3 - 0,2х2 – 0,1х3
х2=1,2 – 0,1х1 – 0,1х3 (4.25)
х3=0,8 + 0,1х1 + 0,1х2
Так как норма матрицы B системы (4.25) удовлетворяет неравенству ||В||<1 (по формуле 4.4), то согласно теореме 1 метод простых итераций для заданной системы сходится. На основе неравенства (4.6) определим величину || 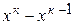 ||. Для этого найдем ||В||=0,3. Тогда ||
||. Для этого найдем ||В||=0,3. Тогда || 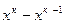 ||£
||£ 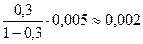 . За нулевое приближение решения системы (4.24) примем: х10=1,3; х20=1,2; х30=0,8. Подставляя эти значения и последующие найденные приближения в (4.3), получим последовательность итераций, которая приведена в табл. 4.1.
. За нулевое приближение решения системы (4.24) примем: х10=1,3; х20=1,2; х30=0,8. Подставляя эти значения и последующие найденные приближения в (4.3), получим последовательность итераций, которая приведена в табл. 4.1.
Таблица 4.1
Решение системы линейных уравнений методом простых итераций
  Номер итерации I Номер итерации I | |||||
| хiк | 1,3 | 0,98 | 0,997 | 1,0009 | 0,99994 |
| х2к | 1,2 | 0,99 | 0,997 | 1,0006 | 0,99997 |
| х3к | 0,8 | 1,05 | 0,997 | 0,9994 | 1,00015 |
Из табл. 4.1 видно, что ||х4 - х3||£0,002, это означает, что приближение х4 имеет предельную абсолютную погрешность 0,005.
Ответ: 0,99989 £ х1 £ 0,99999
0,99972 £ х2 £ 1,00002
1,0001 £ х3 £ 1,00020.
4.4.2. Решить систему линейных уравнений (4.24) методом Зейделя.
Для этого преобразуем систему к сходящемуся виду по формуле теоремы 3 (АТ×А×х= АТ×в). Эквивалентная нормальная система для СЛАУ (4.24) имеет вид:
102×х1+31×х2+х3=134
31×х1+105×х2+2 х3=138 (4.26)
х1+2 х2+102×х3=105.
Приведем систему (4.26) к виду (4.2):
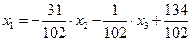
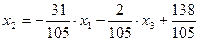 (4.27)
(4.27)
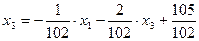 .
.
За нулевое приближение возьмем вектор х0 = {1,3137; 1,3141; 1,0294}. Последующие приближения получаются по формулам (4.7) и приведены в табл. 4.2.
Таблица 4.2
Решение системы линейных уравнений методом Зейделя
 |
  Номер итерац. i Номер итерац. i | |||||
| хiк | 1,3137 | 0,90419 | 0,99157 | 0,99925 | 0,99993 |
| х2к | 1,3143 | 1,02773 | 1,00248 | 1,00022 | 1,00002 |
| х3к | 1,0294 | 1,00040 | 1,00003 | 1,00000 | 1,00000 |
||х4-х3||=0,0002.
4.4.3. Решить систему линейных уравнений (4.24) методом Халецкого.
Результаты расчётов, для удобства, сведены в таблицу (табл.4.3). А теперь рассмотрим формулы (4.9), (4.10) при n=3. По равенствам 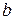 i1 =
i1 = 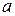 i1, i=1, 2, 3 находится первый столбец матрицы В. Затем по формулам с1j=
i1, i=1, 2, 3 находится первый столбец матрицы В. Затем по формулам с1j= 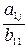 , j= 2, 3 вычисляется первая строка матрицы С. Второй столбец матрицы В находим по формулам:
, j= 2, 3 вычисляется первая строка матрицы С. Второй столбец матрицы В находим по формулам:
bi2 = аi2 –bi1×с12, i =2, 3.
Таблица 4.3
Решение системы линейных уравнений методом Халецкого
| x1 | x2 | x3 | b | х1 | х2 | x3 | b | ∑ | |||||||
| II | a11 | a12 | a13 | a14 | |||||||||||
| a21 | a22 | a23 | a24 | ||||||||||||
| a31 | a32 | a33 | a34 | -1 | -1 | ||||||||||
| II | b11 | c12 | c13 | c14 | 0.200 | 0.100 | 1.3000 | 2.600 | |||||||
| b21 | b22 | c23 | c24 | 1.0000 | 9.8 | 0.0918 | 1.0918 | 2.1837 | |||||||
| b31 | b32 | b33 | c34 | -1.0000 | -0.8000 | 10.1735 | 0.9795 | 2.0000 | |||||||
| III | y1 | x1 | 1.3000 | 1.0000 | |||||||||||
| y2 | x2 | 1.0918 | 1.0000 | ||||||||||||
| y3 | x3 | 1.0000 | 1.0000 | ||||||||||||
Элементы второй строки матрицы В вычисляются из соотношений:
с2j= 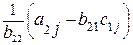 , j=3, 4, 5.
, j=3, 4, 5.
4.4.4. Найти обратную матрицу А-1 методом Халецкого (Самостоятельная работа)
Для матрицы системы (4.24) обратная матрица имеет вид:

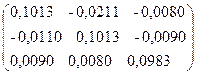
Проверка правильности вычисления А-1 по формуле (4.14) показывает, что матрица вычислена с высокой точностью.
Формулы (4.19) для i=3, n=3 имеют вид:
d31×b11+d32×b21+d33×b31=0
d32×b22+b33×b32=0
d33×b33=1
Решается эта система, начиная с последнего уравнения. Далее используется (4.20) при n=3 и j=3:
d23+d33×c23=0
d13+d23×c12+d33×c13=0.
4.4.5. Найти l1 и х1 матрицы Ат ×А системы линейных уравнений (4.26) (Самостоятельная работа)
В примере рассматривается матрица Ат ×А, т.к. она нормальная. Система (4.22) при n=3, x3=1 и матрице (4.26) имеет вид:
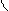 x11=1/l1(102×x11+31×x21+1)
x11=1/l1(102×x11+31×x21+1)
x21=1/l1(31×x11+105x21+2)
l1= (x11+2×x21+102).
Решение её методом простых итераций даёт l1=134,6760 x1={10,5338; 11,0711; 1,0000}. Проверка правильности вычислений по формуле (4.21) показывает, что в l1 и x1 все приведённые знаки верные.
5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
5.1. Цель работы
Овладеть навыками оценки погрешности приближённых величин и сравнения замеров по точности.
5.2. Порядок выполнения задания
1. Вычислить интеграл по формуле трапеций с тремя верными десятичными знаками.
2. Вычислить интеграл по формуле Симпсона при n=8; оценить погрешность результата, составив таблицу конечных разностей. Найти интервалы точного значения интеграла.
2.2. Варианты заданий
№1. 1) 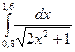 2)
2) 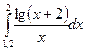
№2. 1) 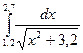 2)
2) 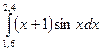
№31) 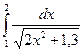 2)
2) 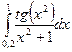
№41) 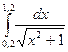 2)
2) 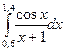
№51) 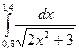 2)
2) 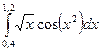
№61) 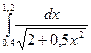 2)
2) 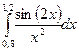
№71) 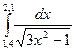 2)
2) 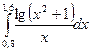
№81) 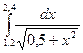 2)
2) 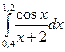
№91) 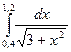 2)
2) 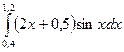
№101) 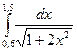 2)
2) 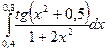
№111) 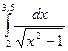 2)
2) 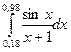
№12 1) 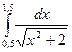 2)
2) 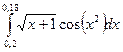
№13 1) 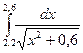 2)
2)