Векторлық өріс. Остроградский-Гаусс теоремасы
Элементар кубтың  тұйықталған беті арқылы өтетін қайсыбір
тұйықталған беті арқылы өтетін қайсыбір 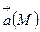 векторлық өрістің
векторлық өрістің  ағынын қарастырайық.Координата осьтерін осы кубтың
ағынын қарастырайық.Координата осьтерін осы кубтың  қабырғаларымен беттесетіндей етіп бағыттаймыз.
қабырғаларымен беттесетіндей етіп бағыттаймыз.

Онда  ағыны кубтың жақтарының әрқайсысынан алынған алты интегралдың қосындысына тең болады. Интегралдық есептеулерден белгілі орта мән туралы теореманы қолдана отырып, осы интегралдардың әрқайсысын сәйкес келетін жақтың ауданы мен
ағыны кубтың жақтарының әрқайсысынан алынған алты интегралдың қосындысына тең болады. Интегралдық есептеулерден белгілі орта мән туралы теореманы қолдана отырып, осы интегралдардың әрқайсысын сәйкес келетін жақтың ауданы мен 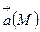 векторының осы жақтағы нормаль құраушысының мәнінің көбейтіндісі түрінде көрсетуге болады.
векторының осы жақтағы нормаль құраушысының мәнінің көбейтіндісі түрінде көрсетуге болады.
Оy осіне перпендикуляр өзара параллель І және ІІ жақтаулар арқылы өтетін векторының ағынын есептейміз. ІІ жақтау арқылы өтетін ағын 
мұндағы  координаталардың І және ІІ жақтардағы орташа мәндері;
координаталардың І және ІІ жақтардағы орташа мәндері;  векторының Оу осіндегі проекциясы.
векторының Оу осіндегі проекциясы.
І және ІІ жақтар арқылы өтетін жалпы ағын:

мұндағы  -элементар кубтың кез-келген нүктесіндегі туынды деп есептеу керек.
-элементар кубтың кез-келген нүктесіндегі туынды деп есептеу керек.
Сонымен, Оу осіне перпендикуляр жақтар арқылы өтетін ағын  -ке тең.
-ке тең.
Осылайша 
мұндағы  -элементар кубтың көлемі
-элементар кубтың көлемі
V көлемді шектен тұрған кез-келген тұйық S бетті қарастырамыз. Өзара перпендикулярдың жазықтықтардың жүйесімен бұл көлемді элементар кубтарға бөлеміз. S бетпен шектесетін шекті элементар кубтардың кубтық формасы болмайтыны анық. Бірақ, арақашықтықтары бұдан да кіші өзара перпендикуляр жазықтықтар жүйесін таңдап алып, шеткі кубтардың жақтарын S бетпен беттесетіндей жағдайға жеткізуге болады.
Әрбір  элементар кубтың тұйық беті арқылы өтетін
элементар кубтың тұйық беті арқылы өтетін 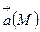 векторлық өрісін есептейміз және барлық элементар кубтар бойынша алынған өрнектерді қосамыз. Сонда
векторлық өрісін есептейміз және барлық элементар кубтар бойынша алынған өрнектерді қосамыз. Сонда

мұндағы  –ші кубтың тұйық беті арқылы өтетін
–ші кубтың тұйық беті арқылы өтетін 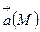 векторының ағыны
векторының ағыны
 -ші элементар кубтың көлемі
-ші элементар кубтың көлемі
Барлық элементар кубтардың жақтарын екі топқа бөлуге болады: практика жүзінде S беттің элементтерімен беттесетін сыртқы жақтар және көршілер кубтарға бір –бірінен бөлетін ішкі жақтар.
 өрнегіне әрбір ішкі жақ арқылы өтетін
өрнегіне әрбір ішкі жақ арқылы өтетін 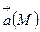 векторының ағыны екі рет қарама –қарсы таңбалармен енеді, себебі осы жақтың бір бетінде жататын куб беті арқылы өтетін және екінші бетінде жататын куб беті арқылы өтетін
векторының ағыны екі рет қарама –қарсы таңбалармен енеді, себебі осы жақтың бір бетінде жататын куб беті арқылы өтетін және екінші бетінде жататын куб беті арқылы өтетін 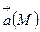 векторының ағындары есептеледі.Осындай қосылғыштардың қарама-қарсы таңбалары көршілес кубтардың жанасатын беттерінің сыртқы нормальдарымен сәйкес келеді. Осылайша, ішкі жақтарға қатысты қосындының барлық
векторының ағындары есептеледі.Осындай қосылғыштардың қарама-қарсы таңбалары көршілес кубтардың жанасатын беттерінің сыртқы нормальдарымен сәйкес келеді. Осылайша, ішкі жақтарға қатысты қосындының барлық  мүшелері өзара қысқарады және бұл қосынды S беттің элементтерімен беттесетін кубтардың сыртқы жақтары арқылы өтетін
мүшелері өзара қысқарады және бұл қосынды S беттің элементтерімен беттесетін кубтардың сыртқы жақтары арқылы өтетін 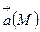 векторының ағындарының қосындысына тең.
векторының ағындарының қосындысына тең.
Ендеше

мұндағы N-S тұйық бет арқылы өтетін 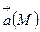 векторының ағыны
векторының ағыны
 (*)
(*)
(*) өрнегі –векторлық формада Остроградский-Гаусс теоремасы: Кез-келген тұйық S бет арқылы өтетін 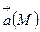 векторлық өрістің ағыны
векторлық өрістің ағыны  –нен осы бетпен шектелген көлем бойынша алынған үш еселік интегралға тең. Сонымен бірге
–нен осы бетпен шектелген көлем бойынша алынған үш еселік интегралға тең. Сонымен бірге 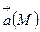 векторлық өрістің
векторлық өрістің  және
және  проекциялары өздерінің дербес туындыларымен бірге беттің ішінде үздіксіз деп есептейміз.
проекциялары өздерінің дербес туындыларымен бірге беттің ішінде үздіксіз деп есептейміз.
Егер 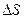 беті, ішіндегі барлық нүктелерде тұрақты деп есептейтіндей, өте кішкентай болса, онда (*) өрнегінде
беті, ішіндегі барлық нүктелерде тұрақты деп есептейтіндей, өте кішкентай болса, онда (*) өрнегінде  -ді интегралдың алдына шығаруға болады. Онда кез-келген формадағы элементар
-ді интегралдың алдына шығаруға болады. Онда кез-келген формадағы элементар  тұйық бет арқылы өтетін N ағын мына формуламен өрнектеледі.
тұйық бет арқылы өтетін N ағын мына формуламен өрнектеледі.
 (**)
(**)
(**) өрнегі дивергенцияның инвариантты анықтамасын береді. M нүктесіндегі 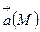 векторлық өрістің дивергенциясы деп M нүктесін қортшап тұрған кез-келген бет арқылы өтетін
векторлық өрістің дивергенциясы деп M нүктесін қортшап тұрған кез-келген бет арқылы өтетін 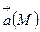 векторлық өрістің ағынының осы бетпен шектелген
векторлық өрістің ағынының осы бетпен шектелген  көлемге қатынасының
көлемге қатынасының  ұмтылғандағы шегін айтады.
ұмтылғандағы шегін айтады.
(**) өрнегінен 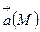 векторлық өрістің дивергенциясы берілген нүктедегі
векторлық өрістің дивергенциясы берілген нүктедегі 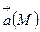 векторлық өрістің ағынының көлемдік тығыздығы болып табылады.
векторлық өрістің ағынының көлемдік тығыздығы болып табылады.
«дивергенция» (divergentia) латын тілінен аударғанда (расхождение, расходимость)
Лекция №3.
Гамильтон операторы. Бірінші реттік дифференциалдық операциялар. Гамильтон операторының скаляр және векторлық өрістердің көбейтіндісіне әсері.
Негізгі дифференциалдық операциялар:
 скаляр өрістің градиенті
скаляр өрістің градиенті
 векторлық өрістің дивергенциясы:
векторлық өрістің дивергенциясы:

 векторлық өрістің құйыны (роторы):
векторлық өрістің құйыны (роторы):

Осы үш дифференциалдық операциялар бір ғана символикалық дифференциалдық оператордың көмегімен жазыла алады. Ол ирланд математигі У.Р.Гамильтонның атымен аталған.
 -Гамильтон операторының белгіленуі («набла»)
-Гамильтон операторының белгіленуі («набла»)
Декарттық координаттар жүйесінде:

 -операторының скаляр әсерін
-операторының скаляр әсерін
 - мен
- мен  көбейтіндісі ретінде қарастырамыз.
көбейтіндісі ретінде қарастырамыз.
 - скаляр өрістің градиенті.
- скаляр өрістің градиенті.
 векторлық оператордың
векторлық оператордың 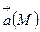 векторымен скаляр көбейтіндісі скалярды береді:
векторымен скаляр көбейтіндісі скалярды береді:

 мен
мен 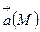 векторының векторлық көбейтіндісі векторға тең:
векторының векторлық көбейтіндісі векторға тең:

Скаляр өрістің  градиентін, сонымен бірге
градиентін, сонымен бірге  Гамилтон операторының координаттар жүйесіне тәуелсіз инвариантты түрде өрнектеуге болады.
Гамилтон операторының координаттар жүйесіне тәуелсіз инвариантты түрде өрнектеуге болады.
Ол үшін тұйық 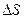 контур бойынша
контур бойынша  интегралды қарастырамыз, мұндағы
интегралды қарастырамыз, мұндағы
 - кез-келген ттаңдауымызша алынған скаляр өріс,
- кез-келген ттаңдауымызша алынған скаляр өріс,  - ауданша векторы.
- ауданша векторы.
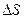 тұйық бет ретінде қабырғалары элементар
тұйық бет ретінде қабырғалары элементар  кубты аламыз: Элементар кубтың жақтарының ауданы аз болғандықтан әрбір жақтың ішінде
кубты аламыз: Элементар кубтың жақтарының ауданы аз болғандықтан әрбір жақтың ішінде  тұрақты деп есептеуге болады.
тұрақты деп есептеуге болады.
Ендеше: 
мұндағы х,у,z –  скаляр өрістің мәндері алынатын М нүктесінің координаттары;
скаляр өрістің мәндері алынатын М нүктесінің координаттары;  - х,у,z координаттардың сәйкес жақтардағы орташа мәндері
- х,у,z координаттардың сәйкес жақтардағы орташа мәндері
 скаляр функцьияларын М(х,у,z) нүктелерінің аймағында қатарға жіктейміз:
скаляр функцьияларын М(х,у,z) нүктелерінің аймағында қатарға жіктейміз:

Сонда
 (*)
(*)
мұндағы  -элементар кубтың көлемі
-элементар кубтың көлемі
(*) формулаға сәйкес Гамильтон операторын былай жазуға болады:

мұндағы  көлемді қамтитын тұйық элементар бет.
көлемді қамтитын тұйық элементар бет.
Алынған өрнек скаляр өрістің градиентінің және Гамильтон операторының интегралдық анықтамасы болып табылады. Бұл анықтамалар инвариантты және кез-келген координаттар жүйесінде қолданады.
Гамильтон операторы бағыт бойынша дифференциалдауды белгілеу үшін де қолданылады.
Кез-келген 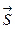 бағыты бойынша туынды:
бағыты бойынша туынды: 
мұндағы  бағытындағы бірлік вектор. Гамильтон операторын қолданып былай жазуға болады:
бағытындағы бірлік вектор. Гамильтон операторын қолданып былай жазуға болады:

мұндағы  операторы –бағыт бойынша дифференциалдау операторы деп аталады.
операторы –бағыт бойынша дифференциалдау операторы деп аталады.
Гамильтон операторының скаляр және векторлық өрістердің көбейтінділеріне қалай әсер ететінің қарастырайық. Бұл жағдайда, берілген набла операторының дифференциалдау операторы екенін және көбейтіндіге дифференциалдау ережесіне бағынатынын ескеру қажет.
 -скаляр функциялар болсын, сонда
-скаляр функциялар болсын, сонда

Лекция №4
