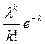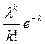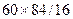| 1. Имеется 6 ключей, из которых только один подходит к замку. Найти закон распределения СВ Х, равной числу проб при открывании замка, если испробованный ключ в последующих пробах не участвует. Построить многоугольник распределения. |
| 2. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,9. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется: а) составить закон распределения дискретной случайной величины X - числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов. |
3. НСВ X задана дифференциальной функцией f(x):  а). Найти функцию распределения СВ Х: F(x).б). Построить графики F(x) и f(x).в). Найти вероятность попадания СВ Х в интервал (-p/3;-p/4).. |
4. Дана интегральная функция распределения:  .Найти: дифференциальную функцию f(x), M(X), s(X), D(X).. |
| 5. Из двух орудий поочередно ведется стрельба по цели до первого попадания одним из орудий. Вероятность попадания в цель первым орудием равна 0,4 вторым - 0,6. Начинает стрельбу первое орудие. Составить законы распределения дискретных случайных величин Х и Y - числа израсходованных снарядов соответственно первым и вторым орудием. |
| 6. Производится три независимых испытания, в каждом из которых вероятность появления события А равна 0,4. Составить закон распределения дискретной случайной величины Х – числа появлений события А в указанных испытаниях. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение Х. |
| 7. В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято 2 детали. Найти закон распределения случайной величины Х, равный числу стандартных деталей в выборке. Построить многоугольник распределения. |
8. НСВ - задана функцией распределения F(x):  а). Найти плотность вероятности СВ X-f(x). б). Построить графики f(x), F(x). в). Найти вероятность попадания СВ X в (0; p/2). |
| 9. Найти: М(X) НСВ X, распределенной равномерно в интервале (2;8); функцию распределения F(x) и функцию плотности вероятности f(x); вероятность попадания НСВ X в интервал (3; 6). |
| 10. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0,001. Найти вероятность того, что за время Т откажут ровно X элементов. Определить закон распределения СВ X и её числовые характеристики. |
| 11. В коробке 7 карандашей, из которых 4 красных. Из этой коробки наудачу извлекается 3 карандаша. а). Найти закон распределения случайной величины Х равной числу красных карандашей в выборке. б). Построить многоугольник распределения. в). Найти вероятность события: 0<x£2. |
| 12. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,001. Найти вероятность того, что среди 250деталей окажется ровно Х бракованных. Определить закон распределения СВ X и её числовые характеристики. |
| 13 Устройство состоит из большего числа независимо работающих элементов с одинаковой (очень малой) вероятностью отказа каждого элемента за время Т. Найти среднее число отказавших за время Т элементов, если вероятность того, что за это время не откажет хотя бы один элемент, равна 0,99. |
| 14. НСВ на всей числовой оси ОХ задана интегральной функцией: F(x)= (1/2)+(1/p)arctg(x).Найти вероятность, что в результате двух испытаний случайная величина примет значение, заключенное в интервале (0;1). |
15.Дана дифференциальная функция непрерывной СВ Х:  Найти: постоянную С, интегральную функцию F(x). |
| 16. Из 25 контрольных работ, среди которых 5 оценены на «отлично» наугад извлекаются 3 работы. Найти закон распределения ДСВ X, если Х-число работ оцененных на «отлично» среди извлеченных. Построить многоугольник распределения. Чему равна вероятность событий х>0. |
| 17. Найти среднее число l бракованных изделий в партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0,95. Предполагается, что число бракованных изделий в рассматриваемой партии распределено по закону Пуассона. |
| 18. В урне 5 белых и 20 черных шаров. Вынули 3 шара. Случайная величина Х - число вынутых белых шаров. Построить ряд распределения величины Х. |
| 19. Дискретная СВ задана законом распределения: Найти интегральную функцию и построить ее график. |
20. Дана дифференциальная функция непрерывной случайной величины Х:  Найти: постоянную С, интегральную функцию F(x). Вероятность попадания СВ Х в интервал (1/2; 3/2). |
| 21. С вероятностью попадания при явном выстреле 0,9 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4-х выстрелов. ДСВ X-число промахов: а). Найти закон распределения X.б). Построить многоугольник распределения.в). Найти вероятность событий: X<2, X£3, 1<X£3. |
| 22. Бросают три монеты. Требуется: а) задать случайную величину X, равную числу выпавших "решёток"; б) построить ряд распределения. |
| 23.НСВ Х имеет плотность вероятности (закон Коши): f(x)= C/(1+x²). Найти: а) постоянную С= const;. б) функцию распределения F(x);в) вероятность попадания в интервал –1<X<1; г) построить графики f(x), F(X). |
24. Найти М(х) и s(x) НСВ, имеющей плотность вероятности: f(x)= 1/(3  ) exp (-(x+2)²/18) Указать интервал, симметричный относительно М(X) в который попадает случайная величина х с вероятностью р=0,9973. |
| 25. Построить ряд распределения числа попаданий мячом в корзину при четырёх бросках, если вероятность попадания равна 0,7. |
| 26.Два стрелка делают по одному выстрелу в мишень. Вероятность попадания для первого стрелка при одном выстреле 0,5, для второго 0,4. ДСВ Х - число попаданий в мишень.а). Найти закон распределения Х.б). Построить многоугольник распределения.в). Найти вероятность X³1. |
| 27. Из партии в 20 изделий, среди которых имеются 4 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа X бракованных изделий, содержащихся в выборке. |
28.НСВ X задана функцией распределения F(x):  а). Найти плотность вероятности СВ Х-f(x). б). Построить графики f(x), F(x).в). Найти вероятность попадания НСВ в интервал (0; 1). |
| 29. М(Х) и s(Х) нормального распределённой СВ Х соответственно равны 10 и 2.Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12,14). |
30. Случайная величина Х задана функцией распределения:  а). Найти плотность вероятности СВ Х-f(x). б). Построить графики f(x), F(x).в). Найти вероятность попадания НСВ в интервал (0; 1). |
| 31. Три стрелка независимо друг от друга сделали по одному выстрелу по мишени. Вероятность попадания для первого стрелка 0,9, для второго 0,8, для третьего – 0,7. Найти закон распределения величины Х – числа попадания в мишень. Построить многоугольник распределения. Чему равна вероятность получения не менее двух попаданий. |
| 32. Случайная величина x распределена равномерно интервале (0, p). Найти закон распределения случайной величины y=cosx. |
| 33. Случайная величина x равномерно распределена на отрезке [1, 3]. Найти плотность вероятности случайной величины y=x2. |
| 34. Дифференциальная функция НСВ Х задана на всей числовой оси ОХ:f(x)= 4C/ (1+x²).Найти постоянный параметр С. |
35.НСВ Х задана интегральной функцией:  Найти вероятность того, что в результате трех испытаний Х примет значение в интервале (-1;1). |
| 36. В первой урне 5 шаров – 2 белых и 3 чёрных. Во второй 3 шара – 1 белый и 2 чёрных. Из первой урны наудачу переложили во вторую 2 шара, после чего, из второй в первую переложили 1 шар. Найти закон распределения случайной величины Х – числа белых шаров в первой урне, после всех перекладываний шаров. Какова вероятность того, что число белых шаров не больше, чем первоначально. Построить многоугольник распределения. |
| 37. Случайную величину Х умножили на k. Как от этого изменяются ее характеристики: 1) математическое ожидание; 2) дисперсия; 3) среднее квадратичное отклонение; 4) второй начальный момент? |
| 38. Функция распределения случайной величины X задана формулой F(x)=A+Barctgx (-¥<X+¥). Найти: а) постоянные А и В;б) плотность вероятности f(x);в) вероятность того, что величина x попадет в отрезок [-1; 1]. |
 39. Случайная величина Х задана интегральной функцией 0, х£2, F(x) = 0,5x-1, 2<x£4, 1, x>4. Найти вероятность того, что в результате испытания Х примет значение: а) меньше 2, б) меньше 3, в) не меньше 3, г) не меньше 5. |
| 40. Дана интегральная функция НСВ Х: 0, x£0, F(x)= sin2x, 0<x£p/4, 1, x>p/4. Найти дифференциальную функцию и вероятность попадания СВ на интервал (p/16;p/8). |
| 41. Вероятность изготовления стандартной детали – 0,98. Для контроля на удачу взято 100 деталей. Найти закон распределения СВ Х, равный числу нестандартных деталей в выборке. Построить многоугольник распределения. Найти вероятность событий: а) в выборке 2 стандартных детали; б) в выборке более 2 стандартных деталей. |
| 42. Найти M(x) числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 50 билетов, причем вероятность выигрыша равна 0,01. |
43. НСВ задана дифференциальной функцией:  в интервале (-с; с),вне этого интервала f(x)=0. Найти вероятность попадания СВ Х в интервал (-с/2;с/2) и функцию распределения F(x). |
| 44. НСВ X распределена нормально с математическим ожиданием m=10. Вероятность попадания СВ Х в интервал (10; 20) равна 0,3. Чему равна вероятность попадания НСВ Х в интервал (0; 10)? |
| 45. Производятся 20 независимых испытаний, в каждом из которых вероятность появления успеха равна 0,2. Найти дисперсию числа появления успеха в этих испытаниях. |
| 46. ДСВ Х – число мальчиков в семьях с 5-тью детьми. Предполагают равновероятное рождение мальчика и девочки. Найти закон распределения. Построить многоугольник распределения. Найти вероятность событий: а) в семье 2-3 мальчика, б) не более 3-х мальчиков, в) более 1 мальчика. |
| 47. При 10 000 бросании монеты "герб" выпал 6400 раз. Следует ли считать, что монета несимметрична? |
| 48. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время t равна 0,01, Используя неравенство Чебышева, оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время t окажется меньше двух. |
49.НСВ задана дифференциальной функцией:  где l>0. Найти вероятность того, что Х примет значение принадлежащее интервалу (2;3). |
50.Случайная величина Х задана дифференциальной функцией:  (распределение Лапласа). Найти математическое ожидание величины Х. |
Св. план 2013 г., поз. 59
Теория вероятностей.
Усл.- печ. л. - 12 Тираж 100 экз. Формат – 
150048, Ярославль, Московский пр-т, д. 151,
Типография Ярославского ж.д. техникума – филиала МИИТ
. Найти: а) вероятность попадания случайной величины Х в интервал 
; б) дифференциальную функцию (функцию плотности вероятностей) 
; в) математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х; г) построить графики функций 
