Атомное ядро. Радиоактивность

16. Массовое число ядра

A = Z + N,

где Z – зарядовое число (число протонов); N – число нейтронов.

17. Основной закон радиоактивного распада

N = N₀ e^–λt,

где N – число ядер, не распавшихся к моменту времени t; N₀ – число ядер в начальный момент времени; λ –– постоянная радиоактивного распада.

18. Число ядер, распавшихся за время t,

ΔN = N₀ – N = N₀ (1 – e^–λt).

Если промежуток времени Δt, за который определяется число распавшихся ядер, много меньше периода полураспада, то число распавшихся ядер можно определить по формуле

ΔN = λ N Δt.

19. Зависимость периода полураспада от постоянной радиоактивного распада

T = ln2/λ = 0,693/ λ.

20. Среднее время жизни радиоактивного ядра

τ = 1/λ.

21. Активность радиоактивного изотопа

A = – dN/dt = λN = A₀ e^–λt,

где dN – число ядер, распадающихся за интервал времени dt; А₀ – активность изотопа в начальный момент времени.

22. Удельная активность изотопа

а = А/m.

23. Дефект массы ядра

Δm = ZM_H + (A – Z) m_n – M,

где Z – зарядовое число; M_H – масса атома водорода, А – массовое число;
m_n – масса нейтрона; М – масса атома.

24. Энергия связи ядра

Е_св = Δm с²,

где Δm – дефект массы ядра; с – скорость света в вакууме.

Примеры решения задач

Пример 1. Кинетическая энергия электрона равна 0.5 МэВ. Определить длину волны де Бройля.

Решение. Так как кинетическая энергия электрона (0.5 МэВ) почти равна его энергии покоя (0.511 МэВ), то скорость электрона близка к скорости света и, следовательно, задачу нужно решать по формулам релятивистской механики.

Длина волны де Бройля выражается формулой

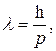(1)

где h – постоянная Планка; p – импульс электрона.

Импульс электрона определим из формулы, связывающей энергию частицы с ее импульсом:

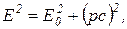(2)

откуда

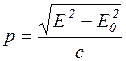. (3)

Полная энергия электрона равна сумме его энергии покоя и кинетической энергии

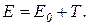(4)

Поэтому

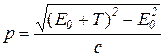
или

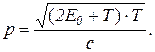(5)

Подставив в формулу (1) вместо импульса р электрона его значение по формуле (5), получим

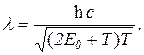(6)

При числовом подсчете по формуле (6) нет необходимости выражать энергию покоя и кинетическую энергию в единицах системы СИ. Значения энергии можно взять в мегаэлектрон-вольтах, если предварительно выразить постоянную Планка в мегаэлектрон-вольтах в секунду:

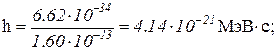
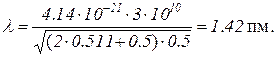
Можно поступить иначе, выразив постоянную Планка h через комптоновскую длину волны λ_k электрона. Как известно, длина волны Комптона

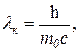
откуда

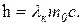(7)

Подставив в формулу (6) вместо h его значение по формуле (7) и учтя, что m₀с² = Е₀, получим

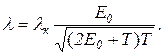(8)

Комптоновская длина волны электрона λ_к = 0.0242 Ǻ. Сделав подстановку чисел, получим искомую длину волны де Бройля:

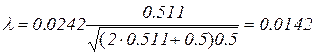Å =1.42 пм.

Пример 2. Угол рассеяния фотона в результате эффекта Комптона составляет 180°. Определить кинетическую энергию электрона отдачи, если энергия фотона до рассеяния равна 0.51 МэВ.

Решение. При эффекте Комптона электрон отдачи получает энергию от фотона

Т = ε₁ – ε₂, (1)

где ε₁ – энергия падающего фотона; ε₂ – энергия рассеянного фотона.

Энергию рассеянного фотона найдем, воспользовавшись уравнением Комптона

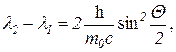
которое для случая рассеяния под углом Θ = 180° примет вид

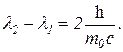
Выразив длины волн через энергию фотонов, получим

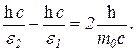
Разделив обе части равенства на hc, найдем

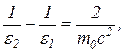
или, приняв во внимание, что m₀с² есть энергия покоя электрона Е₀,

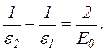
Отсюда

.

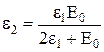Подставив числовые значения ε₁ и Е₀, получим

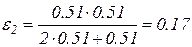МэВ

Подставив значения ε₁ и ε₂ в (1) и произведя вычисления, найдем кинетическую энергию электрона отдачи:

Т = 0.51 – 0.17 = 0.34 МэВ.

Пример 3. Какое наименьшее напряжение надо приложить к рентгеновской трубке, чтобы получить наименьшую длину волны в серии L, если антикатод сделан из железа и постоянная экранирования равна 7.5 (по Мозли)?

Решение. Характеристическое рентгеновское излучение наблюдается всякий раз, когда заполняются места во внутренних слоях электронной оболочки атома, освобожденные электронами вследствие вырывания их бомбардирующими антикатод электронами. Энергия, необходимая для возбуждения какой-либо серии (К, L, М, …), определяется работой вырывания электрона из соответствующего слоя и равна максимальной энергии кванта, соответствующего этой серии.

Так, все линии серии L появляются, если освобождается место во втором от ядра слое – слое L. Следовательно, наименьшую длину волны или максимальную частоту для этой серии определим по формуле Мозли из условия, что n = ∞, k = 2, Z = 26:

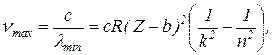
где b – постоянная экранирования. Для этой серии у всех элементов b одинакова и равна 7.5 (по Мозли).

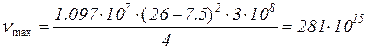Гц.

Из сказанного выше следует, что

eU = hν_max,

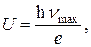
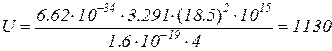В.

При таком напряжении на трубке появятся все линии серии L, и более мягкие, а линии серии K наблюдаться не будут.

Пример 4. Электрон, имеющий скорость 10⁶ м/с, влетает в камеру Вильсона. Приняв размер зерна фотоэмульсии порядка 10^–6 м, найдите неопределенность в скорости. Сравните V_х и ΔV_х.

Решение. Ширина трека 10^–6 м, следовательно, неопределенность в координате Δх = 10^–6. Используя соотношение неопределенности Гейзенберга, запишем

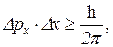
следовательно,

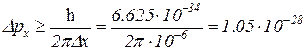кг·(м/с).

Из неопределенности импульса определим неточность в скорости:

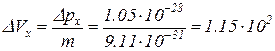м/с,

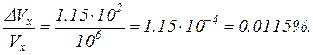
Таким образом, в этом случае можно говорить о траектории частицы в классическом смысле.

Пример 5. Определить возможные значения орбитального момента импульса М_l электрона в возбужденном атоме водорода, если энергия возбуждения ε = 12.09 эВ.

Решение. Орбитальный момент импульса М_l электрона определяется квантовым числом по формуле

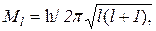
где l – орбитальное квантовое число (l = 0, 1, 2 ,…, n – 1).

Найдем главное квантовое число n с помощью формулы, определяющей собственные значения энергии электрона в атоме водорода:

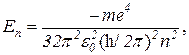
где n – главное квантовое число (n = 1, 2, 3,…).

Учтем, что при n = 1 E = –13.6 эВ. Тогда

.

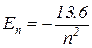Энергия возбуждения ε есть квант энергии, поглощенный атомом при переходе из основного состояния (n = 1) в возбужденное. Следовательно,

E_n – E₁= ε.

Подставив числовые значения величин, выраженные в электрон-вольтах, получим

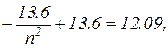
откуда n = 3. Следовательно, l = 0, 1, 2.

Теперь найдем возможные значения М_l:

при l = 0 M_l = 0,

при l = 1 M_l = (h/2π) 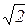= 1.49 × 10^–34 Дж × с,

при l = 2 M_l = (h/2π) 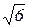= 2.60 × 10^–34 Дж × с.

Пример 6. Первоначально покоившийся атом водорода испустил фотон, длина волны которого соответствует максимальной длине волны в серии Бальмера. Определить скорость V движения атома водорода
(h = 6.62 × 10^–34·Дж × с; М = 1.672 × 10^–24 г; R = 109677 см^–1).

Решение.По закону сохранения импульса, импульс испущенного фотона равен импульсу атома, поэтому

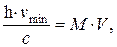
откуда

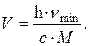
Максимальную частоту фотона можно определить, используя формулу Бальмера для случая n = 3 (длина волны в этом случае будет максимальной):

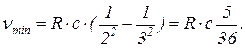
Значит, скорость отдачи

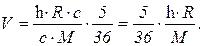
В системе СИ

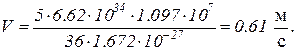
Пример 7. Радиоактивный натрий ₁₁Νa²⁴ распадается, выбрасывая
β-частицы. Период полураспада 14,8 ч. Вычислить количество атомов, распавшихся в 1 мг данного радиоактивного препарата:

а) за 10 ч;

б) за 0,01 с.

Решение.а)Число радиоактивных атомов убывает со временем по закону

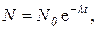
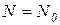
где Ν – число нераспавшихся радиоактивных атомов через t секунд с момента начала отсчета; Ν₀ – число радиоактивных атомов к моменту начала отсчета; λ – постоянная радиоактивного распада.

Число распавшихся атомов

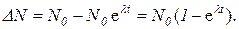(1)

Выразив λ через период полураспада Т, преобразуем выражение е^-λt:

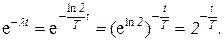
После преобразования равенство (1) будет иметь вид

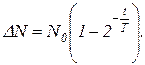(2)

В нашем случае Ν₀ – число атомов в 1 мг ₁₁Νa²⁴. В одном килограмм-атоме ₁₁Νa²⁴ содержится 6.02 × 10²⁶ (число Авогадро) атомов; в 1 мг содержится

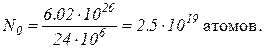
Подставив числовые значения в формулу (2), получим

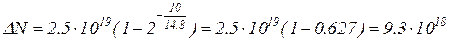атомов.

б)Вторая часть задачи решается аналогично, однако здесь встречаются трудности в вычислении выражения 2^–t/T.

Для решения этой части задачи заметим, что при λΔt<<1 вместо (2) можно воспользоваться соотношением

ΔN = N₀ λ Δt. (3)

Заменив в формуле (3) λ через 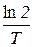и выразив Т в секундах, получим

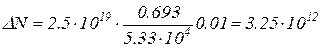атомов.

Пример 8. Найти активность радона, образовавшегося из m₀ = 1 г радия 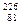Ra за одни сутки. Периоды полураспада радия и радона соответственно равны Т₁ = 1.6 × 10³ лет, Т₂ = 3.8 суток.

Решение.Активность препарата измеряется числом ядер, распадающихся в единицу времени:

,

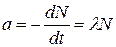где dN – число радиоактивных ядер, распадающихся за промежуток времени dt; λ – постоянная радиоактивного распада.

Если радиоизотоп А₁ с постоянной распада λ₁ превращается в радиоизотоп А₂ с постоянной распада λ₂, то число ядер радиоизотопа А₂ изменяется со временем по закону

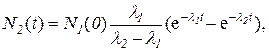
где N₁(0) – число ядер радиоизотопа А₁ в момент t = 0.

Для искомой активности запишем

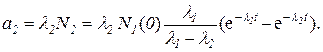
Входящие сюда величины выразим через данные m₀, μ, T₁, T₂ по формулам

T λ = ln2,

N₀ = N_A (m₀/μ),

где N_A – число Авогадро; m₀ – начальная масса препарата; μ – молярная масса изотопа.

Произведя сокращения, имеем

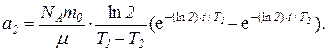
Это общая формула, выражающая закон изменения со временем активности одного радиоизотопа (дочернего), полученного в процессе распада другого (материнского). Формулу можно упростить, если учесть вытекающие из условия соотношения Т₁>>T₂ и T₁>>t. Из первого неравенства следует, что можно пренебречь величиной Т₂ в разности T₁ – T₂. В силу второго неравенства можно принять за единицу первый член, стоящий в скобках. Тогда найдем

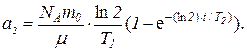
Произведя расчет, получим

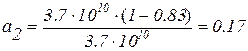Ки.