Умова (3.12) і є умовою паралельності двох прямих

З формули (3.10) також легко отримати умову перпендикуляр­ності двох прямих. Справді, якщо 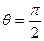, то

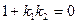
Звідси, якщо прямі перпендикулярні, то

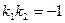або 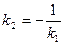(3.13)

У випадку, коли прямі задано загальними рівняннями, то для виведення умови перпендикулярності краще використати формулу (3.11). Дві прямі перпендикулярні 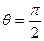, якщо

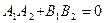(3.14)

Якщо дві прямі задані канонічними рівняннями

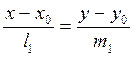та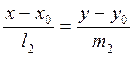

тоді їх умовою перпендикулярності буде:

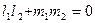
а умовою паралельності буде:

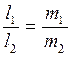
Кут між двома прямими, що задані канонічно:

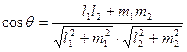
4. Нехай задано пряму L. Через початок О системи координат проведемо нормаль до прямої і позначимо кут нахилу нормалі до вісі Ох через 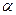, точку її перетину з прямою L - через М_о. а довжину відрізка ОМ₀ - через р. Напрям прямої від О до М_о будемо вважати додатним. Величини 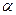і р цілком визначають положення прямої L на площині.

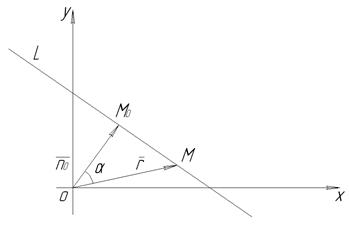
Рис. 7

Позначимо через М довільну точку прямої L, орт нормалі – через 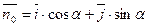. Спроектуємо радіус - вектор 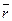точки М на нормаль.

,

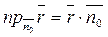Але 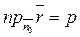. Отже,

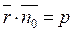(3.15)

Виразимо скалярний добуток (3.15) двох векторів через їх координати. Дістанемо рівняння

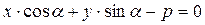(3.16)

Рівняння (3.16) називають нормальним рівнянням прямої.Нехай задано рівняння прямої у загальному вигляді

Ах+Ву+С=0. (3.17)

Потрібно звести це рівняння до нормального.

У зв'язку з тим, що рівняння (3.16) і (3.17) є дві різні форми рівняння тієї самої прямої, то випливає

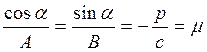
Звідси

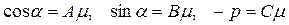
Знайдемо коефіцієнт пропорційності :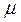

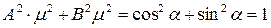
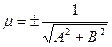(3.18)

Знак 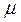із-за умови 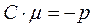має бути протилежний знаку С.

Отже, помноживши загальне рівняння прямої (3.17) на 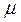отримаємо її нормальне рівняння:

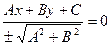(3.19)

Тепер, використовуючи рівняння (3.16) прямої у нормальному вигляді, знайдемо відстань від заданої точки до заданої прямої (рис. 8).

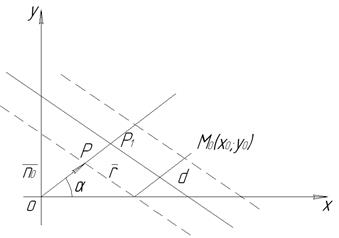
Рис. 8

Нехай пряму Lзадано нормальним рівнянням

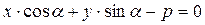
Проведемо через точку 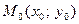прямої, що паралельна L. Її рівняння запишемо у нормальному вигляді; знаючи, що обидві прямі відрізняються тільки відстанню від початку координат:

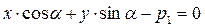(3.19)

Але, 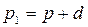. Тому, враховуючи, що пряма (3.19) проходить через точку М₀(х₀; у₀), отримаємо

.

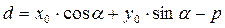Якщо точка 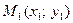лежить між початком координат і прямою, то 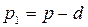. Тоді

.

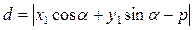У загальному випадку відстань точки від прямої записуємо так:

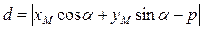(3.20)

Якщо рівняння прямої задано у загальному вигляді, то

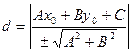
Контрольні питання

1. Як записати рівняння прямої, що проходить через задануточку перпендикулярно до заданого вектора?

2. Який вигляд має загальне рівняння прямої на площині?

3. Як записати рівняння прямої, що проходить через початок координат?

4. Як записати рівняння прямої, що паралельна вісі Ох? вісі Оу?

5. Як записати рівняння прямої з кутовим коефіцієнтом?

6. Як записати рівняння прямої, що проходить через задану точку у заданому напрямі?

7. Як записати рівняння прямої, що проходить через дві задані точки?

8. Який вигляд має канонічне рівняння прямої?

9. Як знайти кут між двома прямими?

10 Які умови перпендикулярності і паралельності двох прямих?

11. Який вигляд має нормальне рівняння прямої?

12. Як звести загальне рівняння прямої до нормального?

13. Як знайти відстань від точки до прямої?

Рекомендована література

1. П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова „Высшая математика в упражнениях и задачах” Ч1. М.1986

2. В.Ю.Клепко, В.Л.Голець „Вища математика в прикладах і задачах” К. 2006.

3. Клетеник Д.В. Сборник задач по аналитической геометрии, -М.: Наука, 1978.

4. За редакцією В.П.Дубовика І.І.Юрика „Вища математика. Збірник задач.” К. 2001.

5. Под редакцией Н.И.Кремера «Высшая математика для экономистов.» М. 2000.

6. Под редакцией В.И.Ермакова «Общий курс высшей математики для экономистов» М. 2000.

7. Под редакцией В.И.Ермакова «Сборник задач по высшей математики для экономистов» М. 2002.

8. В.В.Барковський, Н.В.Барковська „Вища математика для економістів” (теорія) К. 2005.

9. В.В.Барковський, Н.В.Барковська „Вища математика для економістів” (практика) К. 2005

10. За редакцією Ю.К. Рудавського „Збірник задач з лінійної алгебри та аналітичної геометрії” Л. „Бескит Біт” 2002.