Решение матричных уравнений

Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15).

Возможны два случая: 1) матрица А квадратная невырожденная; 2) матрица А - либо вырожденная, либо прямоугольная.

1) Если А – квадратная и|А| ¹ 0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А^-1×В и Х = В×А^-1 соответственно, если эти произведения определены. И не имеют решения, если они не определены.

2) А – квадратная матрица, но |А| = 0, либо А - прямоугольная матрица. Если матрица А имеет размерность m´n, а матрица В – размерность р´к, то, при m ¹ р уравнение (14) не имеет решения, а при n ¹ к не имеет решения уравнение (15). Если же m = р , то в уравнении (14) матрица Х должна иметь к столбцов, а в уравнении (15) она должна иметь р строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений.

Пример 5. Найдите матрицу Х, если А×Х = В, где А = 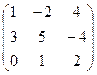, В = .

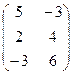Из примера 5 следует, что матрица А имеет обратную, поэтому Х = А^-1×В. Используя найденную в примере 5 матрицу А^-1, получим Х = × = = .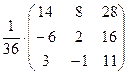

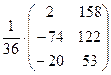Пример 6. Найдите матрицу Х, если Х×А = В, где А = 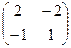, В = 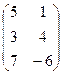. Так как |А| = 0, то для А обратной матрицы нет.По правилам умножения матриц, в матрице В столько строк, сколько их в матрице Х, и столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х = 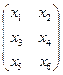. Тогда Х×А = 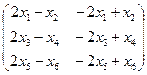. Полученная матрица равна матрице В тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений.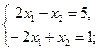 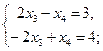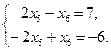Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.

IV. ЛИНЕЙНЫЕ ПРОСТРАНСТВА

Алгебраические операции

Пусть дано некоторое множество М. Будем говорить, что на множестве М задана внутренняя алгебраическая операция, если задан закон (правило), по которому каждой упорядоченной паре элементов а и в из М ставится в соответствие вполне определённый элемент с. Если при этом для любой пары элементов а, в из М соответствующий элемент с всегда тоже принадлежит М, то М замкнуто относительноданной операции.

Пусть даны два множества М и К. Будем говорить, что на множестве М задана внешняя алгебраическая операция, если задан закон, по которому для каждой пары элементов а Î М, в Î К ставится в соответствие вполне определённый элемент с Î М.

Сложение и умножение действительных чисел – примеры внутренних алгебраических операций на множестве действительных чисел. Умножение вектора на действительное число – пример внешней алгебраической операции на множестве векторов трёхмерного евклидова пространства.

Пусть на множестве элементов Р определены две внутренние алгебраические операции: сложение и умножение: при сложении каждой упорядоченной паре элементов а и в из Р взаимнооднозначно соответствует элемент с Î Р(с = а + в); при умножении тоже каждой упорядоченной паре элементов а и в из Р взаимнооднозначно соответствует элемент с Î Р(с = а×в).

Определение 12. Множество элементов Р называется полем, если на нём заданы две алгебраические операции: сложение и умножение, удовлетворяющие следующим требованиям (аксиомам):

1. Р замкнуто относительно обеих операций;

2. а + в = в + а для любых элементов а и в из Р (коммутативный закон для сложения);

3. (а + в) + с = а + (в + с) для любых элементов а, в и с из Р (ассоциативный закон);

4. $ 0 Î Р такой, что а + 0 = а для любого а Î Р;

5. для любого а Î Рсуществует (-а) Î Р такой, что а + (-а) = 0;

6. а×в = в×а для любых элементов а и в из Р (коммутативный закон);

7. (а×в)×с = а×(в×с) для любых элементов а, в и с из Р (ассоциативный закон);

8. $ е Î Р такой, что е×а = а для любого а Î Р(е называетсяединицей и обозначается 1);

9. для любого а Î Рсуществует а^-1Î Р такой, что а×а^-1 = е (а^-1 – обратный элемент для а);

10. (а + в)×с = а×с + в×с для любых элементов а, в и с из Р.

Примерами полей являются множество рациональных чисел ( R ), множество действительных чисел (Q ), множество комплексных чисел (С ).