В слабых полях
В постоянном или достаточно медленно меняющемся от времени внешнем электрическом поле при достаточно малой величине напряженности этого поля, вектор поляризации P, как правило (исключение составляют сегнетоэлектрики), линейно зависит от вектора напряженности поля E:
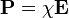 (в системе СГС),
(в системе СГС),
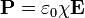 (в системе СИ; дальше формулы в этом параграфе приводятся только в СГС, формулы СИ и дальше отличаются лишь электрической постоянной
(в системе СИ; дальше формулы в этом параграфе приводятся только в СГС, формулы СИ и дальше отличаются лишь электрической постоянной 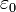 )
)
где 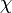 — коэффициент, зависящий от химического состава, концентрации, структуры (в том числе от агрегатного состояния) среды, температуры, механических напряжений и т. д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды. Для однородной среды фиксированного состава и структуры в фиксированных условиях ее можно считать константой. Однако в связи со всем сказанным выше вообще говоря
— коэффициент, зависящий от химического состава, концентрации, структуры (в том числе от агрегатного состояния) среды, температуры, механических напряжений и т. д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды. Для однородной среды фиксированного состава и структуры в фиксированных условиях ее можно считать константой. Однако в связи со всем сказанным выше вообще говоря 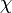 зависит от точки пространства, времени (явно или через другие параметры) и т. д.
зависит от точки пространства, времени (явно или через другие параметры) и т. д.
Для изотропных[1] жидкостей, изотропных твердых тел или кристаллов достаточно высокой симметрии 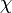 — просто число (скаляр). В более общем случае (для кристаллов низкой симметрии, под действием механических напряжений и т. д.)
— просто число (скаляр). В более общем случае (для кристаллов низкой симметрии, под действием механических напряжений и т. д.) 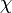 — тензор (симметричный тензор второго ранга, вообще говоря невырожденный), называемый тензором поляризуемости. В этом случае можно переписать формулу так (в компонентах):
— тензор (симметричный тензор второго ранга, вообще говоря невырожденный), называемый тензором поляризуемости. В этом случае можно переписать формулу так (в компонентах):
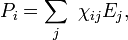
где величины со значками соответствуют компонентам векторов и тензора, соответствующим трем пространственным координатам.
Можно заметить, что поляризуемость — одна из наиболее удобных физических величин для простой иллюстрации физического смысла тензоров и применения их в физике.
Как и для всякого симметричного невырожденного тензора второго ранга, для тензора поляризуемости можно выбрать (если среда неоднородная — то есть тензор зависит от точки пространства — то по крайней мере локально, если же среда однородная, то и глобально) т. н. собственный базис — прямоугольные декартовы координаты, в которых матрица 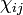 становится диагональной, а тогда — только в этих координатах(!) — запись немного упрощается:
становится диагональной, а тогда — только в этих координатах(!) — запись немного упрощается:
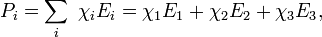
где 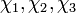 — три собственных числа тензора поляризуемости.
— три собственных числа тензора поляризуемости.
Если все эти три собственных числа равны друг другу, значит умножение на тензор эквивалентно умножению на число, а среда изотропна (в отношении поляризуемости). (Отсюда ясно, почему кристалл с высокой симметрией не может давать анизотропии: требованиям симметрии могут удовлетворить только три одинаковых собственных числа).
