Исходные данные для задач 1, 2, 3
Таблица 1
| i | хi | у - объем продаж (десятков тыс. руб./день) по вариантам | |||||||||||||
| А | - | А | Б | В | Г | Д | Е | К | Л | М | Н | О | П | Р | |
Продолжение табл. 1
| i | хi | у - объем продаж (десятков тыс. руб./день) по вариантам | |||||||||||||
| Е | А | Б | В | Г | Д | Е | Ж | К | Л | М | Н | О | П | Р | |
Продолжение табл. 1
| i | хi | у - объем продаж (десятков тыс. руб./день) по вариантам | |||||||||||||
| И | А | Б | В | Г | Д | Е | Ж | К | Л | М | Н | О | П | Р | |
Продолжение табл. 1
| i | хi | у - объем продаж (десятков тыс. руб./день) по вариантам | |||||||||||||
| О | А | Б | В | Г | Д | Е | Ж | К | Л | М | Н | О | П | Р | |
Продолжение табл. 1
| i | хi | у - объем продаж (десятков тыс. руб./день) по вариантам | |||||||||||||
| Я | А | Б | В | Г | Д | Е | Ж | К | Л | М | Н | О | П | Р | |
Таблица 2
Исходные дополнительные данные для задачи 2
| i | х2 – площадь паркинга (десятки автомашин) по вариантам | |||||
| - | А | Е | И | О | Я | |
4. Примеры решения задач
Задача №1
Решить задачу №1 по данным варианта из табл 1.
1.1. Нанести в координатах ХY точки на плоскость (построить корреляционное поле).
Решение. Для наглядности выберем наши данные из табл.1. в табл. 3.
Таблица 3
| xi | |||||||
| yi |
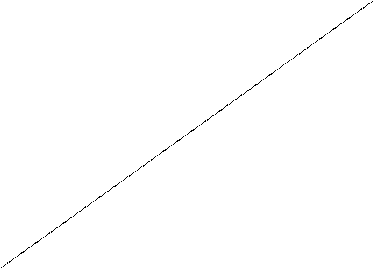
На рис. 1 представлено корреляционное поле. Как видно, оно должно хорошо аппроксимироваться прямой линией. Зависимость между Х и Y тесная и прямая.
| у |  | |||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| х | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
Рис. 1
1.2. Найти методом наименьших квадратов уравнение регрессии Y по Х в линейной форме:
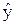 =b0+ b1x. =b0+ b1x. | (1) |
Решение. Расчетные формулы для неизвестных параметров регрессии:
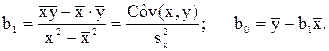 (2)
(2)
На основе табл. 3 рассчитаем необходимые суммы, входящие в формулу (2).
Таблица 4
| xi | yi | x2 | xiyi | (xi- 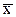 )2 )2 | 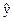 xi xi | ei2=( 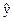 xi-yi)2 xi-yi)2 |
| 5,90 | 1,97 | 0,00 | ||||
| 5,90 | 1,97 | 1,06 | ||||
| 2,04 | 3,51 | 0,22 | ||||
| 0,18 | 5,05 | 0,00 | ||||
| 0,32 | 6,59 | 2,53 | ||||
| 2,46 | 8,13 | 1,28 | ||||
| 20,88 | 12,75 | 1,56 | ||||
| 37,68 | 6,65 |
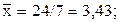 | 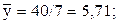 | 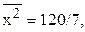 | 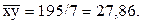 | (3) |
Искомые оценки параметров регрессии и само уравнение регрессии:
b1= (27,86-3,43×5,71)/(17,14-3,432) =8,27/5,38=1,54 b0=5,71-1,54×3,43=0,43 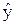 =0,43+1,54x. =0,43+1,54x. |
1.3. Построить линию регрессии на координатной плоскости XY.
Решение. Искомую линию проще всего построить по двум точкам (см. рис. 1), например (0; 0,43) и (8,00; 12,75).
1.4. Показать графически и аналитически, что линия регрессии проходит через точку ( 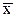 ,
, 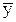 ).
).
Решение. Из графика на рис.1 видно, что линия регрессии проходит через точку “средних” ( 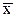 =3,43;
=3,43; 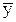 =5,71). Проверим это аналитически:
=5,71). Проверим это аналитически: 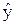 =0,43+1,54×3,43 = 5,71, что и требовалось доказать.
=0,43+1,54×3,43 = 5,71, что и требовалось доказать.
1.5. На сколько вырастет средний объем продаж при увеличении х на 1.
Решение. При увеличении торговой площади на 1 (100 м2) в среднем объем продаж увеличится на b1= 1,54 (т.е. на 15400 руб./день).
1.6. Имеет ли смысл свободный член в уравнении регрессии.
Решение. Свободный член b0=0,43 смысла не имеет, т.к. при нулевой торговой площади положительного объема продаж быть не может.
1.7. Вычислить коэффициент корреляции между переменными X и Y.
Решение. Используем формулу:
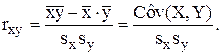 (4)
(4)
Здесь известно все, кроме
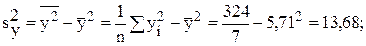
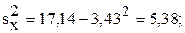
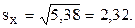
Окончательно 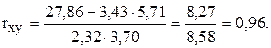
Полученное значение коэффициента корреляции говорит о высокой (почти функциональной) зависимости объема продаж от размера торговой площади.
1.8. Определить графически и аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х=11 (напомним, что это 1100 м2).
Решение. Прогнозное значение из рис.1 и из формулы совпадают:
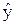 =0,43+1,54×11=17,37 (173700 руб./день)
=0,43+1,54×11=17,37 (173700 руб./день)
1.9, а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж.
Решение. Оценка значения условного МО Мх=11(Y) равна 17,37. Чтобы построить доверительный интервал для СВ 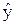 х=11, нужно оценить дисперсию ее оценки
х=11, нужно оценить дисперсию ее оценки 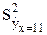 .
.
Для этого определим дисперсию возмущений (см. табл. 4, графы 4-6):
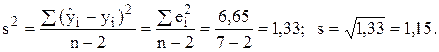
Искомая дисперсия
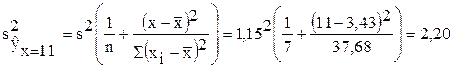
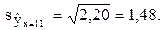
Для статистики Стьюдента 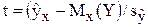 число степеней свободы k = n – 2 = 7 – 2 = 5. По табл. П2 находим значение t0,95;5=2,57 критерия Стьюдента. Искомый 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ":
число степеней свободы k = n – 2 = 7 – 2 = 5. По табл. П2 находим значение t0,95;5=2,57 критерия Стьюдента. Искомый 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ":
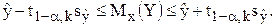
Нижнее значение интервала: 17,37-2,57×1,48=13,57.
Верхнее значение интервала: 17,37+2,57×1,48=21,37.
Окончательно интервал имеет вид:
13,57 £ Mx(Y) £ 17,37.
1.9, б). Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж 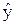 xo=11.
xo=11.
Решение. Чтобы построить доверительный интервал для СВ 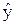 хo=11, нужно оценить ее дисперсию:
хo=11, нужно оценить ее дисперсию:
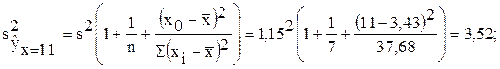
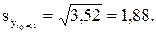
Нижнее значение интервала: 17,37-2,57×1,88=12,54.
Верхнее значение интервала: 17,37+2,57×1,88=22,20.
Окончательно интервал имеет вид:
12,54 £ 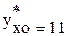 £ 22,20.
£ 22,20.
Как и следует из теории, этот интервал больше предыдущего и большой по величине. Коэффициент осцилляции для него:
Ко=(R/ 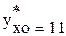 )100%= ((22,2-12,54)/17,37)100%=55,6%.
)100%= ((22,2-12,54)/17,37)100%=55,6%.
1.10, а) Найти с надежностью 0,95 интервальные оценки коэффициента регрессии b1.
Решение. Общая формула для расчета интервала:
b1-D £ b1 £ b1+D,
где 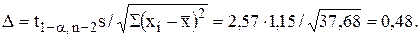
Нижнее значение интервала: 1,54-0,48=1,06.
Верхнее значение интервала: 1,54+0,48=2,02.
Окончательно интервал имеет вид:
1,06 £ b1 £ 2,02.
1.10, б) Найти с надежностью 0,95 интервальные оценки дисперсии возмущений s2.
Решение. Найдем по табл.П3 (критерий Пирсона) табличное значение статистики хи-квадрат: 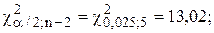
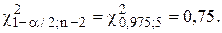
Формула для доверительного интервала:
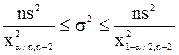
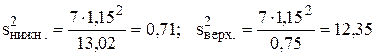
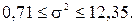
1.11, а) Оценить на уровне a=0,05 значимость уравнения регрессии Y по Х по критерию Фишера.
Решение. Вычислим суммы квадратов.
Общая сумма:
Q=å(yi- 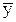 )2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47.
)2=13,77+7,35+2,93+0,51+0,51+1,67+68,73= 95,47.
Регрессионная сумма:
QR=å( 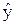 i-
i- 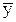 )2=13,99+13,99+4,84+0,44+0,78+8,56+49,56=92,16.
)2=13,99+13,99+4,84+0,44+0,78+8,56+49,56=92,16.
Остаточная сумма: Qe=å( 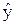 i-у)2=6,65 (см. табл. 4).
i-у)2=6,65 (см. табл. 4).
Значение статистики Фишера :
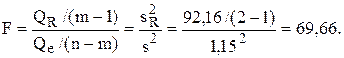
Уравнение регрессии значимо, если F > Fa,k1,k2, где степени свободы k1=m-1=2-1=1, k2=n-m=7-2=5. По табл. П4 находим критическое значение F0,05;1;5=6,61. Так как 69,66 > 6,61, то уравнение значимо: коэффициент регрессии b1 =1,54 значимо отличается от нуля.
1.11, б) Оценить на уровне a=0,05 значимость уравнения регрессии Y по Х по критерию Стьюдента.
Решение. Уравнение парной регрессии значимо, если t>tкрит. Значение статистики Стьюдента:
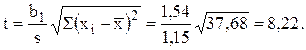
По табл. П2 находим tкрит.=t0,95;7-2=5=2,57. Так как 8,22 > 2,57, то гипотезу Но(Но : β1=0) отвергаем и принимаем противоположную гипотезу Н1: уравнение значимо.
1.12. Определить коэффициент детерминации R2 и раскрыть его смысл: на сколько процентов в среднем объем продаж зависит от размера торговой площади.
Решение. Используем формулу: R2= QR/Q = 92,16 / 95,47 = 0,97. R2 показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной. Ответ: эта доля составляет 97%.
Задача №2
Решить задачу №2 по данным варианта из табл. 1 и 2.
2.1) Нанести в координатах х2у точки на плоскость (построить корреляционное поле).
Решение. Для наглядности выберем наши данные из табл. 1 и 2. Из рис. 2 видно, что прямая линия хорошо аппроксимирует связь между у и х2. Эта связь прямая и очень тесная.
| у |  | ||||||
 15 15 |  | ||||||
 | |||||||
 |  | ||||||
  | |||||||
 |  | х2 | |||||
Рис. 2
2.2. Записать для своего варианта матрицу Х значений объясняющих переменных (матрицу плана).
Решение. См.среднюю матрицу в п. 2.4.
2.3. Записать транспонированную матрицу плана 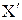 .
.
Решение. См. левую матрицу в п. 2.4.
2.4. Найти произведение матриц 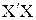 .
.
Решение.
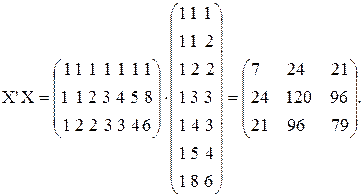
2.5. Найти обратную матрицу ( 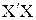 )-1.
)-1.
Решение. Для краткости введем обозначение: А= 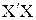 . требуется найти обратную матрицу А-1. Используем формулу:
. требуется найти обратную матрицу А-1. Используем формулу:
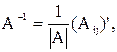
где 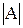 - определитель матрицы А,
- определитель матрицы А,
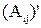 – транспонированная матрица, составленная из алгебраических дополнений матрицы А.
– транспонированная матрица, составленная из алгебраических дополнений матрицы А.
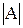 =7×120×79+24×96×21+21×96×24-21×120×21-96×96×7-79×24×24=192.
=7×120×79+24×96×21+21×96×24-21×120×21-96×96×7-79×24×24=192.
Находим алгебраические дополнения:
| А11 = 120 × 79 – 96 × 96 =264; | А12 = -(24 × 79 – 96 × 21) = 120; |
| А13 = 24 × 96 – 120 × 21 = -216; | А21 = -(24 × 79 – 21 × 96) = 120; |
| А22 = 7 × 79 - 21 × 21 = 112; | А23 = -(7 × 96 – 24 × 21)= -168; |
| А31 = 24 × 96 – 21 × 120 = -216; | А32 = -(7 × 96 – 21 × 24) = -168; |
| А33 = 7 × 120 – 24 × 24 = 264. |
Обратная матрица:
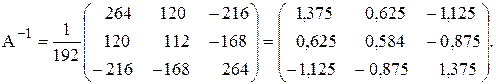
Проверка. Если расчеты верны, то должно выполниться равенство:
А А-1 = Е.
Для повышения точности множитель 1/192 введем отдельно.
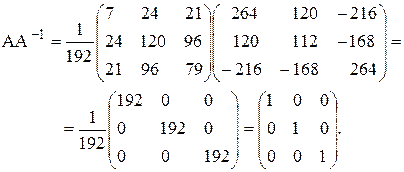
Как видно, равенство выполнено, значит расчет обратной матрицы выполнен верно.
2.6. Найти произведение матриц 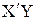 .
.
Решение.
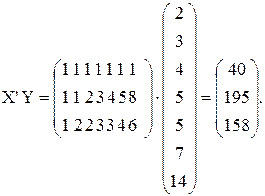
2.7. Найти уравнение регрессии Y по Х1 и Х2 в форме 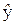 =b0+ b1 х1 + + b2х2 методом наименьших квадратов путем умножения матрицы (
=b0+ b1 х1 + + b2х2 методом наименьших квадратов путем умножения матрицы ( 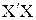 .)-1 на матрицу
.)-1 на матрицу 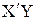 , т.е. рассчитать коэффициенты регрессии по формуле b=(
, т.е. рассчитать коэффициенты регрессии по формуле b=( 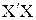 )-1
)-1 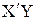 .
.
Решение.
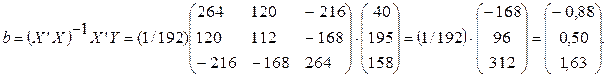
Итак, ответ: b0 = -0,88; b1 = 0,50; b2 = 1,63. Уравнение множественной регрессии имеет вид: 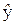 = -0,88 + 0,50x1 + 1,63x2.
= -0,88 + 0,50x1 + 1,63x2.
2.8. Объяснить смысл изменения значения коэффициента регрессии b1.
Решение. В задаче №1 значение b1=1,54, а теперь его значение снизилось до b1=0,50. Это связано с тем, что на объем продаж помимо торговой площади теперь влияет учитываемая площадь паркинга.
2.9. Рассчитать значения коэффициентов эластичности для обоих факторов и сравнить влияние каждого из них на средний объем продаж.
Решение. Коэффициент эластичности в общем случае есть функция объясняющей переменной, например: 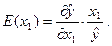
Если 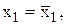
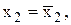 то
то 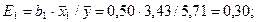 при увеличении х1 от среднего на 1% объем продаж возрастет на 0,30%. Аналогично
при увеличении х1 от среднего на 1% объем продаж возрастет на 0,30%. Аналогично 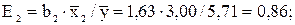 при увеличении х2 от среднего на 1% объем продаж возрастет на 0,86%.
при увеличении х2 от среднего на 1% объем продаж возрастет на 0,86%.
2.10. Оценить аналитически прогнозное среднее значение объема продаж для проектируемого магазина "СИ" с торговой площадью х1=11 (1100 м2) и паркинговой площадью х2 = 8 (80 автомашин).
Решение. Объем продаж рассчитаем по уравнению регрессии:
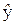 = -0,88 + 0,50 × 11 + 1,63 × 8 = 17,66.
= -0,88 + 0,50 × 11 + 1,63 × 8 = 17,66.
2.11, а) Найти 95%-ный доверительный интервал для среднего прогнозного значения объема продаж магазина "СИ".
Решение. По условию нужно оценить значение Мх(Y), где вектор переменных 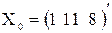 . Выборочной оценкой условного МO Мх(Y) является значение регрессии
. Выборочной оценкой условного МO Мх(Y) является значение регрессии 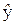 (11, 8) = 17,66. Для построения доверительного интервала для Мх(Y) нужно знать дисперсию оценки
(11, 8) = 17,66. Для построения доверительного интервала для Мх(Y) нужно знать дисперсию оценки 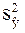 и дисперсию возмущений s2:
и дисперсию возмущений s2:
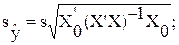
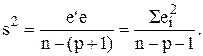
Для удобства вычислений составим табл. 5.
Таблица 5
| i | xi1 | xi2 | yi | 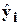 | ei | 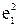 |
| 1,25 | 0,75 | 0,56 | ||||
| 2,88 | 0,12 | 0,02 | ||||
| 3.38 | 0,62 | 0,39 | ||||
| 5.51 | -0,51 | 0,26 | ||||
| 6,01 | -1,01 | 1,02 | ||||
| 8,14 | -1,14 | 1,30 | ||||
| 12,90 | 1,10 | 1,21 | ||||
| ∑ | 40,07 | -0,07 | 4,76 |
На основе табличных данных:
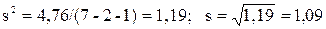
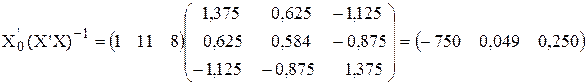
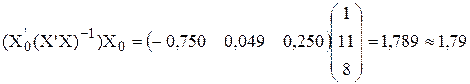
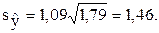
По табл. П2 находим критическое значение статистики Стьюдента t0,95; 7-2-1=5 = 2,78. Полуинтервал D = t0,95; 5∙ 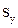 = 2,78 × 1,46 = 4,05.
= 2,78 × 1,46 = 4,05.
Нижняя граница интервала: 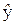 min =
min = 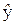 Xo - D = 17,66 - 4,05 = 13,61.
Xo - D = 17,66 - 4,05 = 13,61.
Верхняя граница интервала: 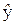 mах =
mах = 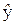 Xo + D = 17,66 + 4,05 = 21,71. Окончательно доверительный интервал для среднего прогнозного значения
Xo + D = 17,66 + 4,05 = 21,71. Окончательно доверительный интервал для среднего прогнозного значения 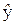 Xo : 13,61 £ МХo(Y) £ 21,71. Интервал большой, что объясняется слишком короткой выборкой.
Xo : 13,61 £ МХo(Y) £ 21,71. Интервал большой, что объясняется слишком короткой выборкой.
2.11, б) Найти 95%-ный доверительный интервал для индивидуального прогнозного значения объема продаж магазина "СИ" 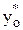 .
.
Решение. Интервал рассчитаем по выражению:
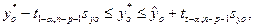
где 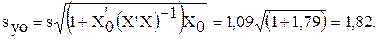
Полуинтервал D = 2,78 × 1,82 = 5,06. Нижние и верхние границы интервала: 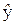 min = 17,66 - 5,06 = 12,60 и
min = 17,66 - 5,06 = 12,60 и 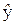 max = 17,66 + 5,06 = 22,72. Окончательно интервал имеет вид: 12,60 £
max = 17,66 + 5,06 = 22,72. Окончательно интервал имеет вид: 12,60 £ 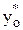 £ 22,72. Как и следовало ожидать, данный индивидуальный интервал больше предыдущего среднего.
£ 22,72. Как и следовало ожидать, данный индивидуальный интервал больше предыдущего среднего.
2.12. Проверить значимость коэффициентов регрессии.
Решение. Стандартная ошибка рассчитывается по формуле:
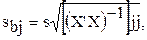
где выражение под корнем есть диагональный элемент матрицы 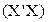 -1.
-1.
Отсюда: sb1 = 1,09 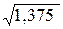 = 1,28; sb2 =1,09
= 1,28; sb2 =1,09 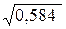 = 0,83.
= 0,83.
Так как t = çb1ç/ sb1 = 0,50/1,28 = 0,39 < t0,95;4 = 2,78, то коэффициент b1незначим (незначимо отличается от нуля).
Так как t = çb2ç/ sb2 = 1,63/0,83 = 1,96 < t0,95;4 = 2,78, то и коэффициент b2 незначим на 5%-ном уровне.
2.13. Найти с надежностью 0,95 интервальные оценки коэффициентов регрессии b1 и b2 и дисперсии s2.
Решение. Интервалы коэффициентов регрессии рассчитываются по формуле: bj + t1-a,n-p-1sbj £ bj £ bj + t1-a,n-p-1sbj.
Поскольку оба коэффициента регрессии незначимы, то не имеет смысла строить для них доверительные интервалы.
2.14. Определить множественный коэффициент детерминации и проверить значимость уравнения регрессии на уровне a=0,05.
Решение. Коэффициент детерминации рассчитывается по формуле:
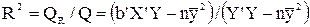

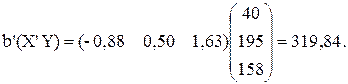
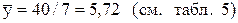 ;
; 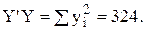
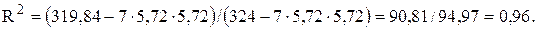
Уравнение регрессии значимо, если (критерий Фишера):
F = R2 (n-p-1)/(1- R2) p > Fa;k1;k2.
Отсюда F = 0,96(7-2-1)/(1-0,962)2 = 24,62 > F0,05;2;4.
Вывод: уравнение значимо.
2.15. Определить, существенно ли увеличилось значение коэффициента детерминации при введении в регрессию второй объясняющей переменной.
Решение. Значения коэффициентов детерминации для регрессий с одной и с двумя объясняющими переменными соответственно равны: R2 = 0,97 и R2 = 0,96. Увеличения значения не произошло. Введение второй переменной не увеличило адекватность модели.
Задача №3
Решить задачу №3 по данным табл. 1 и 2.
3.1. Выписать из табл. 1 временной ряд и построить график в координатах уt (см. табл. 6 и рис. 3).
Таблица 6
| t1 | |||||||
| yi |
3.2. Найти среднее ряда 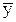 и среднеквадратическое отклонение st, нанести их на график (рис. 3, табл. 6).
и среднеквадратическое отклонение st, нанести их на график (рис. 3, табл. 6).
| у |  | |||||||
 | ||||||||
 | ||||||||
| st = 3,69 | ||||||||
 | ||||||||
 |  | st = 3,69 | ||||||
 |  | |||||||
 | T | |||||||
 | ||||||||
Рис. 3
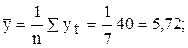
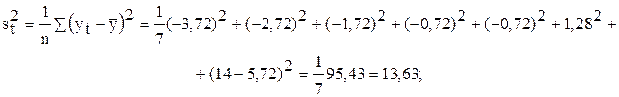
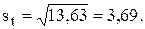
3.3. Найти коэффициенты автокорреляции для лагов τ = 1;2.
Решение. Расчет выполним по формуле
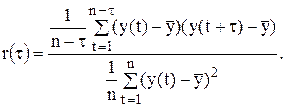
Для τ = 1 и наших значений формула примет вид:
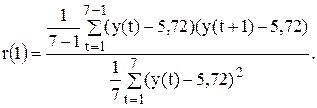
Все промежуточные расчеты см. в табл. 7. Окончательно:
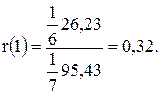
Аналогично для r(2), см. табл. 8:
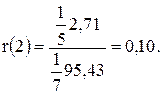
Таблица 7
τ = 1
| t | y(t) | y(t+τ) | y(t)- 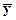 ( ( 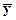 =5,72) =5,72) | y(t+τ)- 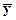 | (y(t)- 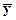 ) · (y(t+τ)- ) · (y(t+τ)- 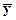 ) ) | (y(t)- 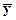 )2 )2 |
| -3,72 | -2,72 | 10,12 | 13,84 | |||
| -2,72 | -1,72 | 4,68 | 7,40 | |||
| -1,72 | -0,72 | 1,24 | 2,96 | |||
| -0,72 | -0,72 | 0,52 | 0,52 | |||
| -0,72 | 1,28 | -0,92 | 0,52 | |||
| 1,28 | 8,28 | 10,60 | 1,64 | |||
| - | - | - | - | - | 68,56 | |
| - | - | 26,23 | 95,43 |
Таблица 8
τ = 2
| t | y(t) | y(t+τ) | y(t)- 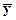 ( ( 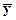 =5,72) =5,72) | y(t+τ)- 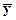 | (y(t)- 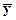 ) · (y(t+τ)- ) · (y(t+τ)- 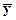 ) ) | (y(t)- 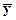 )2 )2 |
| -3,72 | -1,72 | 6,40 | 13,84 | |||
| -2,72 | -0,72 | 1,96 | 7,40 | |||
| -1,72 | -0,72 | 1,24 | 2,96 | |||
| -0,72 | 1,28 | -0,92 | 0,52 | |||
| -0,72 | 8,28 | -5,96 | 0,52 | |||
| - | - | - | - | - | 1,64 | |
| - | - | - | - | - | 68,56 | |
| - | - | 2,71 | 95,43 |
3.4. Построить по трем точкам (0,00; 1,00), (1,00; 0,32), (2,00; 0,10) коррелограмму.
Решение. См. рис. 4.
 | |||||||||||
| r | |||||||||||
 1,0 1,0 | |||||||||||
| 0,8 | |||||||||||
| 0,6 | |||||||||||
| 0,4 | |||||||||||
| 0,2 |  | ||||||||||
 |  |  | τ | ||||||||
Рис. 4. Коррелограмма
5. Тесты по курсу "Эконометрика"
Сокращения:
МНК – метод наименьших квадратов,
НЗР – нормальный закон распределения,
СВ – случайная величина,
СКО – среднеквадратическое отклонение.
1. Регрессионная зависимость Мх(Y) = f(x) - это:
а) зависимость, при которой каждому значению переменной Х соответствует определенное условное математическое ожидание (среднее значение) СВ Y;
б) зависимость между СВ Х и СВ Y;
в) функциональная зависимость Y от СВ Х;
г) статистическая зависимость между СВ Х и СВ Y.
2. Поле корреляции - это:
а) регрессионная зависимость;
б) функциональная зависимость;
в) графическое представление статистической зависимости;
г) графическое представление регрессионной зависимости.
3. Критерий оптимальности метода наименьших квадратов:
а) минимум отклонений наблюденных значений от теоретических;
б) максимум отклонений наблюденных значений от теоретических;
в) минимум отклонений модулей наблюденных значений от теоретических;
г) минимум квадратов отклонений наблюденных значений от теоретических.
4. Доверительный интервал прогноза тем меньше, чем:
а) больше выборка;
б) больше значения результирующей переменной;
в) больше уровень значимости a;
г) больше дисперсия возмущений.
5. Несмещенной называется оценка, у которой:
а) минимальная дисперсия параметра;
б) максимальное математическое ожидание параметра;
в) максимальная дисперсия параметра;
г) математическое ожидание равно оцениваемому параметру.
6. Состоятельной называется оценка, для которой:
а) математическое ожидание равно оцениваемому параметру;
б) выполняется закон больших чисел: оценка сходится по вероятности к оцениваемому параметру;
