Методы оценки адекватности модели

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

Научное исследование синхронного двигателя

шаровой мельницы типа ДМН244-60

Преподователь А.Н. Филатов

Студент ФЭ16 – 08М С.А. Тимченко

Красноярск 2017

Теория.

1)Планирование Эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

2)Чтобы узнать число различных состояний, достаточно число уровней факторов возвести в степень числа факторов 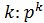, где 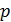- число уровней.

3)Метод наименьших квадратов - математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор X в смысле максимальной близости векторов Y и f(X), или максимальной близости вектора отклонений 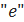к нулю.

4)Полный факторный эксперимент (ПФЭ) — совокупность нескольких измерений, удовлетворяющих следующим условиям:

· Количество измерений составляет 2ⁿ, где n — количество факторов;

· Каждый фактор принимает только два значения — верхнее и нижнее;

· В процессе измерения верхние и нижние значения факторов комбинируются во всех возможных сочетаниях.

Преимуществами полного факторного эксперимента являются

· простота решения системы уравнений оценивания параметров;

· статистическая избыточность количества измерений, которая уменьшает влияние погрешностей отдельных измерений на оценку параметров.

Методы оценки адекватности модели

Первый вопрос, который нас интересует после вычис­ления коэффициентов модели, это проверка ее пригод­ности. Мы будем называть такую проверку провер­кой адекватности модели.

Для характеристики среднего разброса относительно линии регрессии вполне подходит остаточная сумма квад­ратов. Неудобство состоит в том, чтоона зависит от чис­ла коэффициентов в уравнении: введите столько коэф­фициентов, сколько вы провели независимых опытов, и получите остаточную сумму, равную нулю. Поэтому предпочитают относить ее на один «свободный» опыт. Число таких опытов называется числом степеней свобо­ды f.

Числом степеней свободы в статистике называется разность между числом опытов и числом коэффициентов (констант), которые уже вычислены по результатам этих опытов независимо друг от друга.

Остаточная сумма квадратов, деленная на число сте­пеней свободы, называется остаточной диспер­сией, или дисперсией адекватности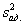

.

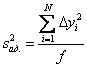В статистике разработан критерий, который очень удобен для проверки гипотезы об адекватности модели. Он называется F-критерием Фишера и определяется сле­дующей формулой:

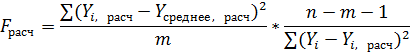
И сравнивается с .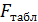

Если:

,

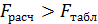То модель считается адекватной.