Допускающие понижение порядка

ДУ n – порядка имеет вид: .

Если его можно разрешить относительно старшей n-й производной, то уравнение примет вид:

(*)

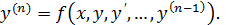Далее будем рассматривать ДУ высших порядков типа (*).

Теорема (о существовании и единственности решения). Если в ДУ (*) функция f и ее частные производные по аргументам y, y’, …, y^{(n - 1)} непрерывны в некоторой области, содержащей точку x = x₀, y = y₀, y’ = y’₀, …, y ^{(n - 1)} = y₀^{(n - 1)}, то существует и при том единственное решение уравнения (*), удовлетворяющее условиям

.

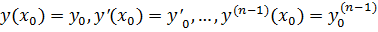Рассмотрим уравнения высших порядков, допускающие понижения порядка.

1. Уравнение вида: 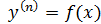(в уравнении нет y, y’, …, y^{(n - 1)})

Интегрируя по х левую и правую части получим

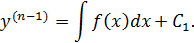
Снова интегрируем

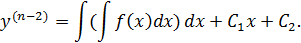
И так далее

…

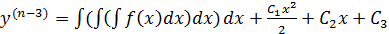После n-интегрирований получим общее решение.

Пример.

Найти частное решение уравнения 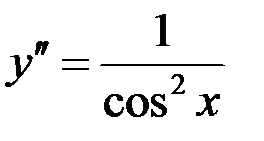, удовлетворяющее начальным условиям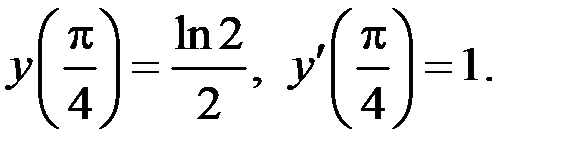

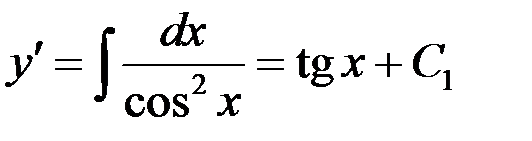
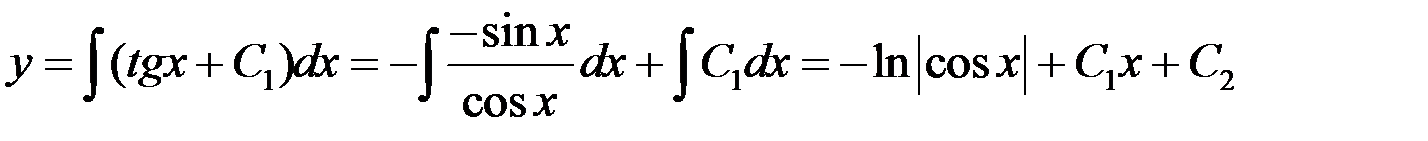– общее решение.

Для нахождения частного решения подставим начальные условия:

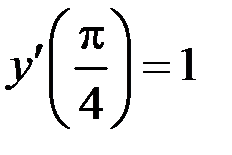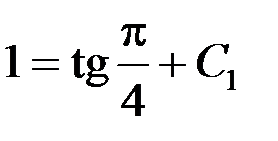: Þ С₁ = 0

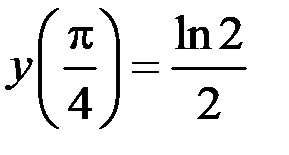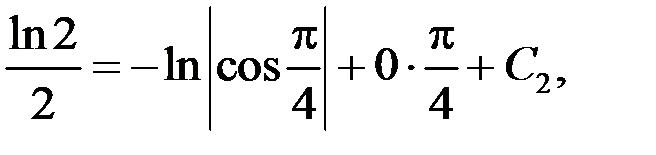
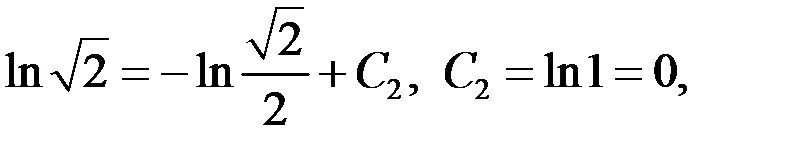
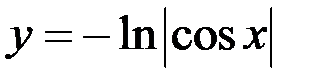: – частное решение, удовлетворяющее заданным начальным условиям.

2. Уравнение вида: 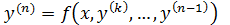(уравнение не содержит явно y и может не содержать производных до порядка
(k – 1) включительно)

Такое уравнение допускает понижение порядка на k-единиц введением новой искомой функции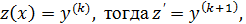
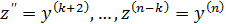. Исходное уравнение примет вид: 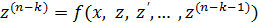– это ДУ (n – k) – порядка. Решив последнее уравнение получим общее решение: 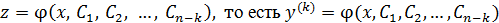– это уравнение k-го порядка вида 1, решая его k-кратным интегрированием получим общее решение исходного уравнения.

Пример.

Найти общее решение уравнения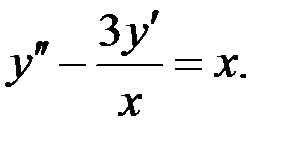

Вводим новую функцию: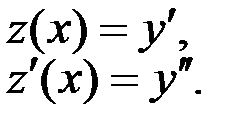

Тогда уравнение примет вид 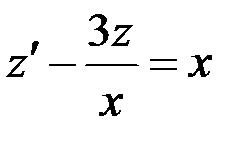– это ЛНДУ первого порядка. Решение будем искать в виде 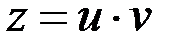, при этом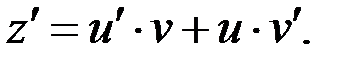

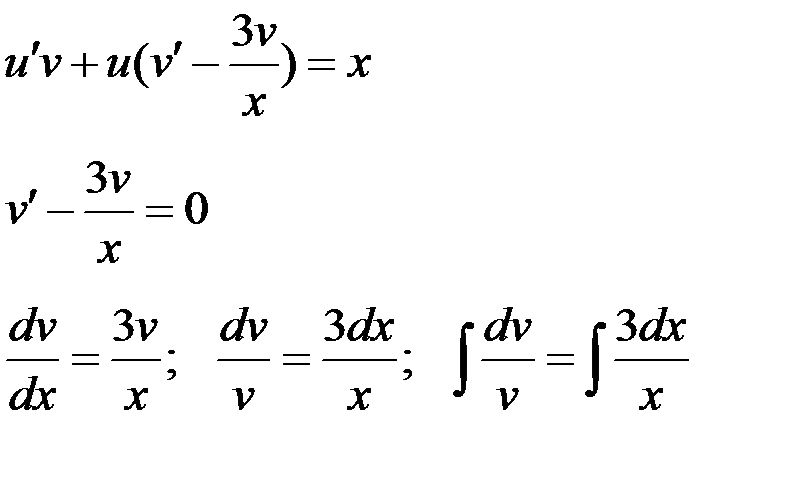
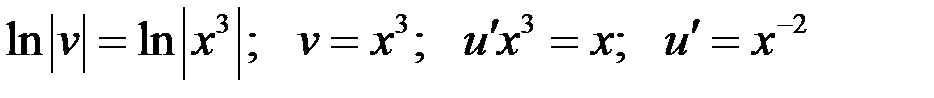
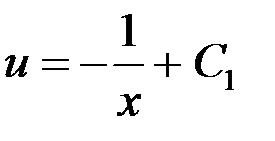
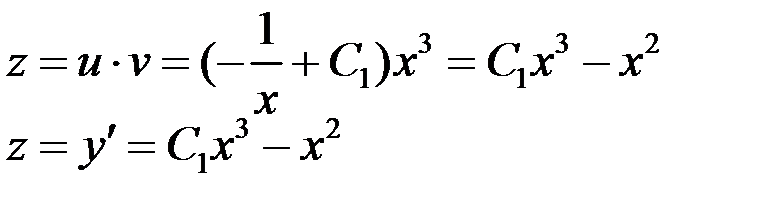
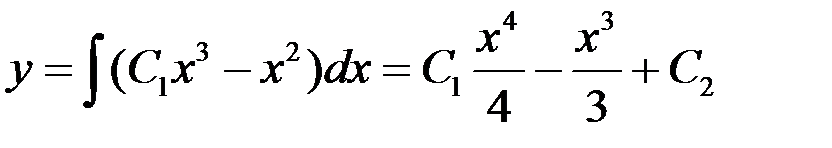
3. Уравнение вида: 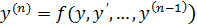(уравнение не содержит явно независимой переменной х)

Решаем заменой:

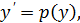тогда

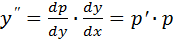
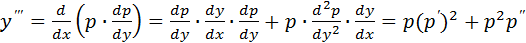и так далее.

Таким образом, порядок уравнения понижается на 1.

Пример.

Найти общее решение уравнения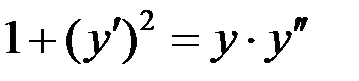

Делаем подстановку: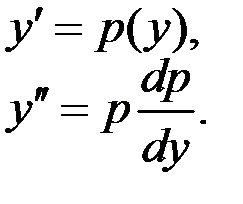

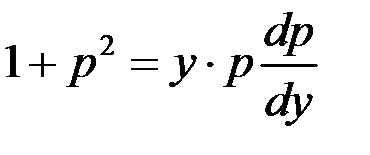– это уравнение с разделяющимися переменными.

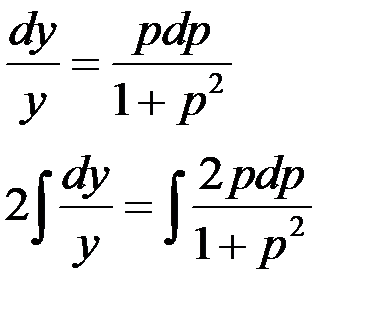
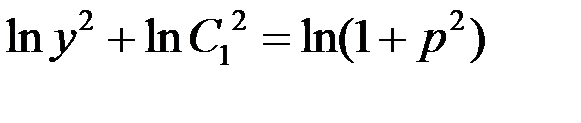
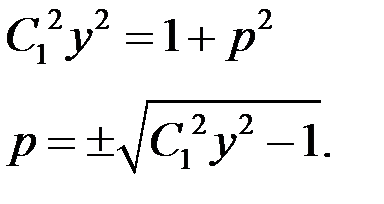
Тогда

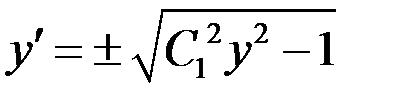
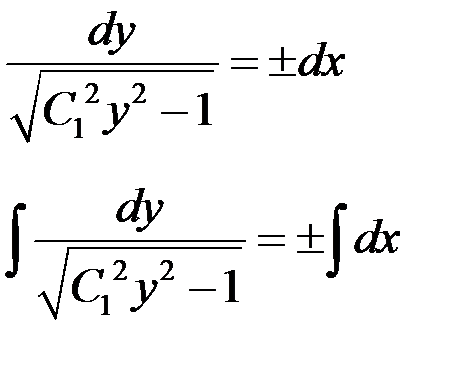
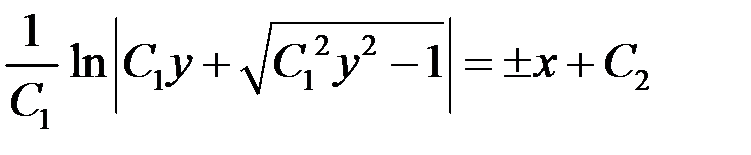– общий интеграл исходного уравнения.

Решение примерного варианта

Контрольной работы

Задача 1

Найти общее решение дифференциального уравнения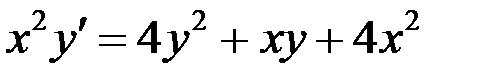

Решение

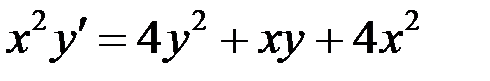Поделим на 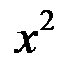, получим

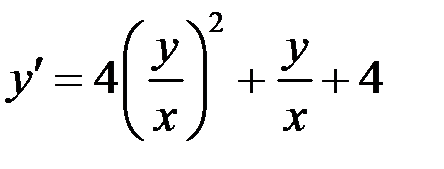
Правая часть является однородной функцией нулевой степени, так как

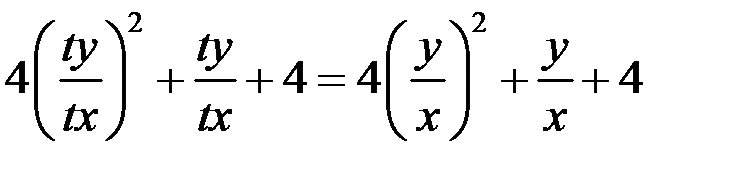
Следовательно, исходное уравнение является однородным.

Делаем замену , .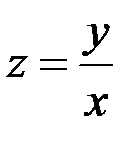

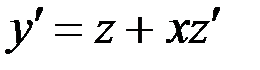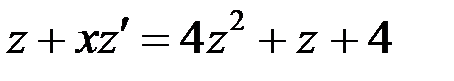
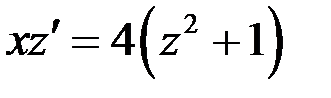
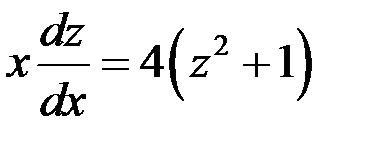
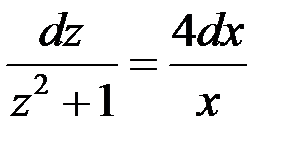
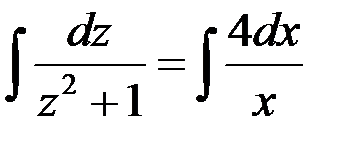
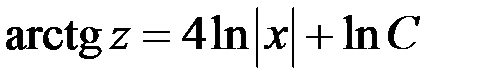
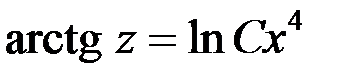
Подставим 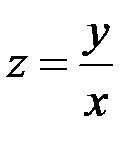, тогда 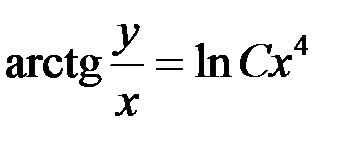- общий интеграл.

Ответ: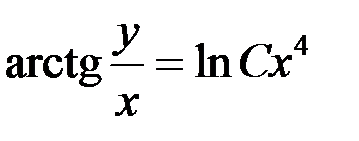

Задача 2

Решить уравнение и сделать проверку: .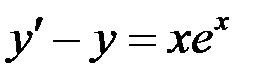

Решение

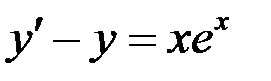- это линейное дифференциальное уравнение первого порядка.

Делаем замену .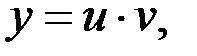

(*)

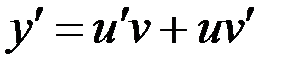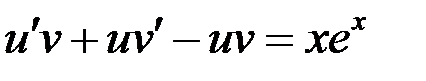
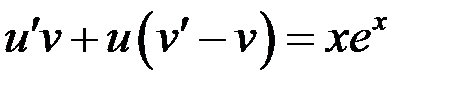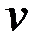– будем искать из условия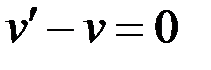

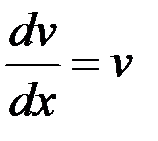
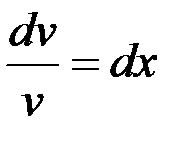
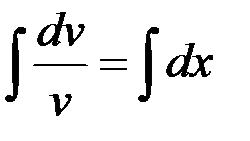
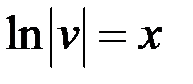(считаем постоянную равной 0, так как ищем одну из первообразных)

Тогда 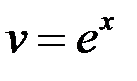. Подставим 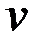в уравнение (*)

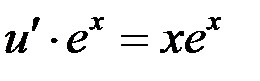
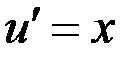
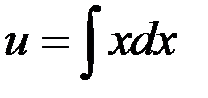
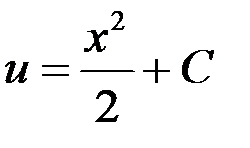
Тогда 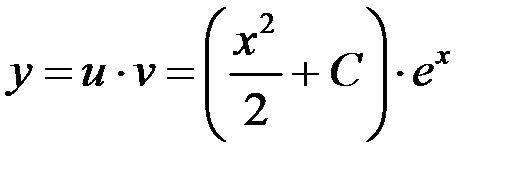- общее решение.

Проверка: подставим 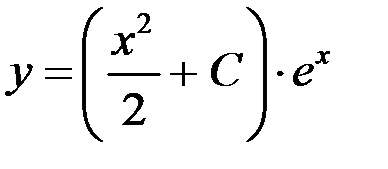в исходное уравнение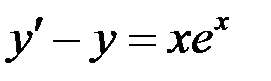

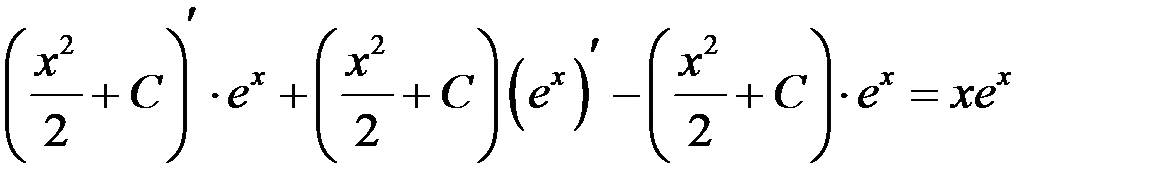
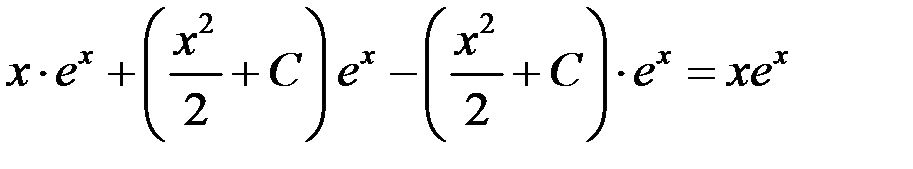
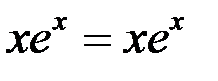– верно.

Ответ: .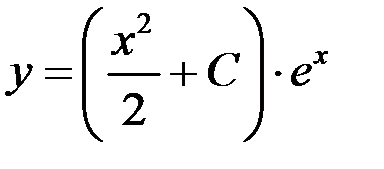

Задача 3

Решить задачу Коши: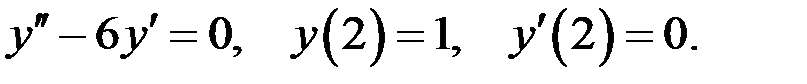

Решение

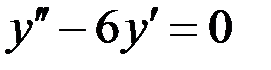- ЛОДУ второго порядка с постоянными коэффициентами.

Составим характеристическое уравнение:

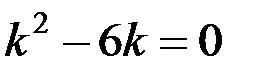
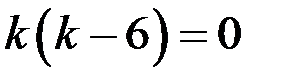
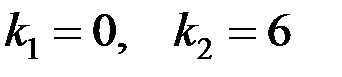Тогда общее решение имеет вид:

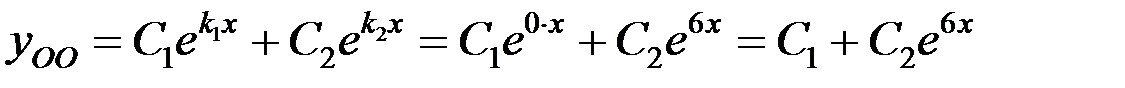
Найдем производную:

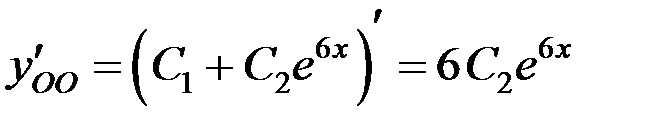
Подставим начальные условия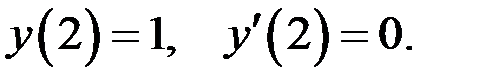

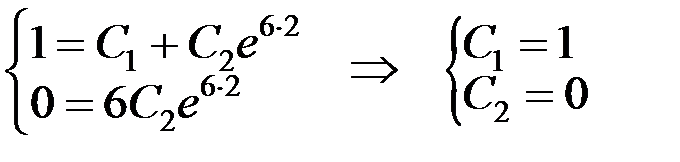
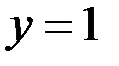– частное решение, удовлетворяющее заданным начальным условиям.

Ответ: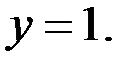

Задача 4

Найти общее решение дифференциального уравнения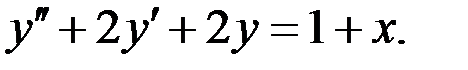

Решение

Это ЛНДУ второго порядка с постоянными коэффициентами с правой частью специального вида.

Составим соответствующее ЛОДУ:

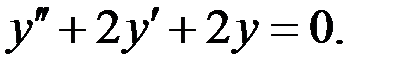
Тогда характеристическое уравнение будет:

.

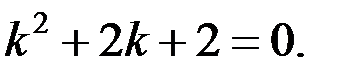
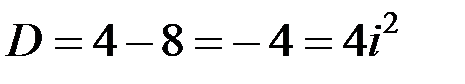
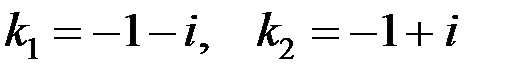Следовательно, 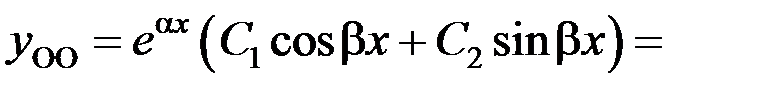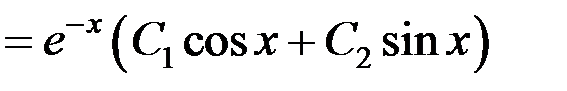– общее решение однородного уравнения.

Найдем частное решение неоднородного уравнения. Так как 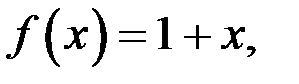то частное решение 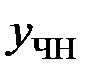будем искать в виде: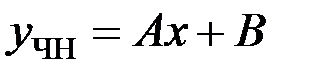

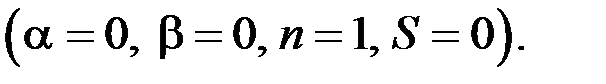
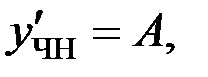
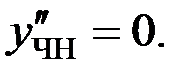
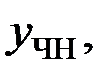
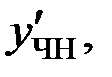
Подставим 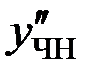в исходное уравнение для нахождения неопределенных коэффициентов:

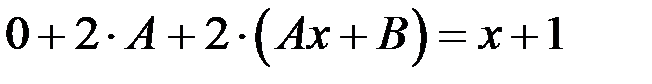
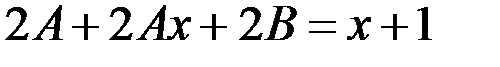
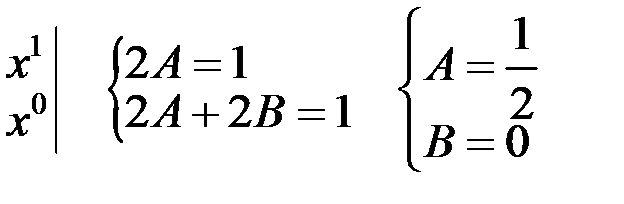
Следовательно,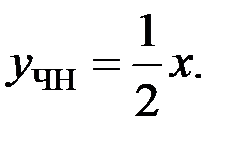

Так как 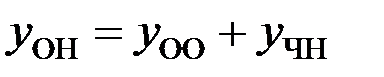, то 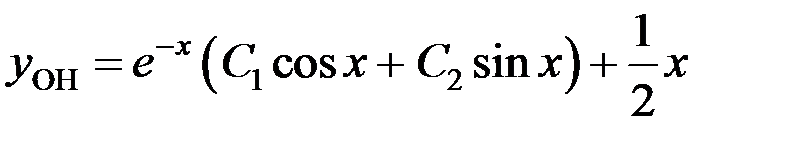– общее решение исходного уравнения.

Ответ: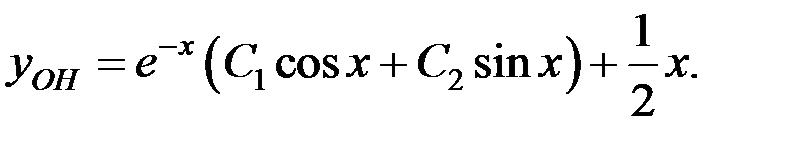

Задача 5

Указать вид общего решения, не находя неопределенных коэффициентов: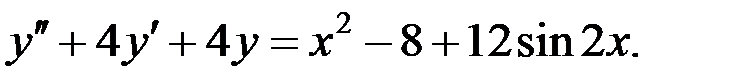

Решение

Это ЛНДУ второго порядка с постоянными коэффициентами с правой частью специального вида. Соответствующее ЛОДУ имеет вид:

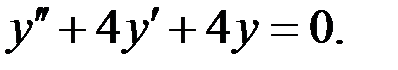
Характеристическое уравнение:

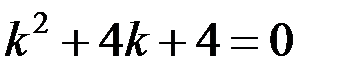
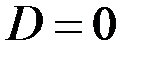
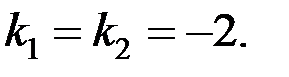
Тогда 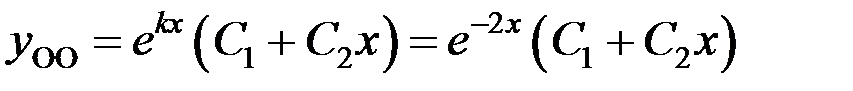– общее решение однородного уравнения.

Найдем частное решение неоднородного уравнения.

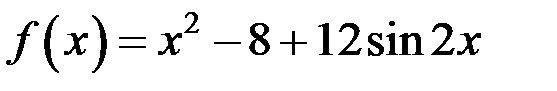
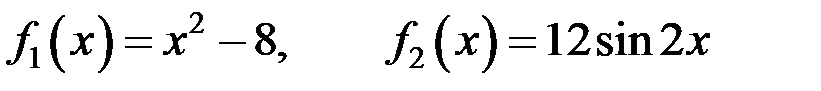
Так как 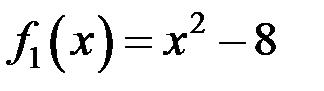, то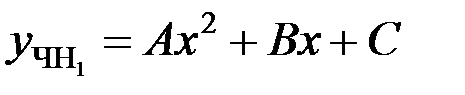

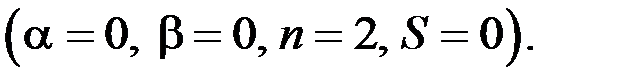
Так как 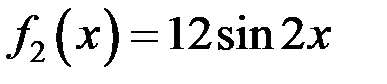, то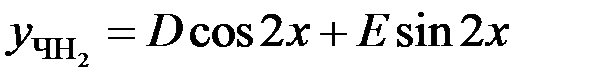

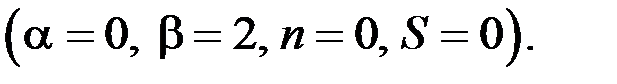
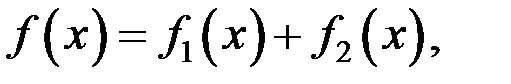поэтому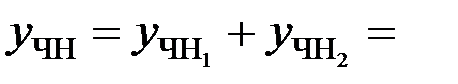

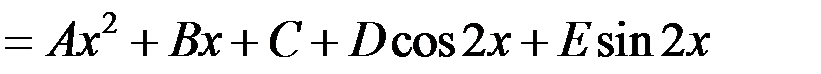
Так как, 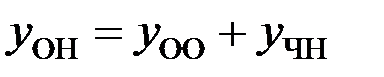, то 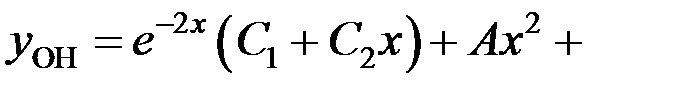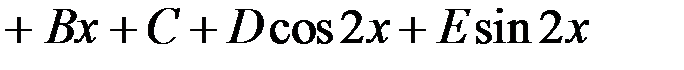– общее решение исходного уравнения.

Ответ: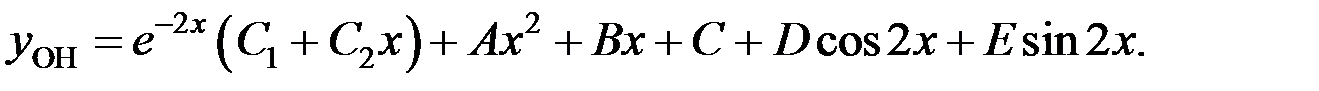

Список литературы

Основная литература

1. Кремер Н.Ш. Высшая математика для экономистов: Учебник. – М.: ЮНИТИ, 2000.

2. Шипачев В.С. Высшая математика: Учебник для вузов. – М.: Высш. шк., 2001.

Дополнительная литература

1. Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для втузов. – М., 2004.

2. Шипачев В.С. Задачник по высшей математике. – М.: Высш. шк., 2001.

Оглавление

Введение .............................................................................................. 3

Контрольная работа 3.1. Дифференциальное исчисление функций нескольких переменных ............................................................................................... 3

Контрольная работа 3.2. Дифференциальные уравнения .............. 21

Список литературы .............................................................................. 44

Печатается в авторской редакции

Технический редактор М.Н. Авдюхова

Лицензия А № 165724 от 11.04.06 г.

Подписано в печать 15.03.12 г. Формат 60 ´ 84 ¹/₁₆ .

Гарнитура таймс. Уч.-изд. л. 1,5. Усл. п.л. 3,2.

Тир. 4. Зак.

ФГБОУ ВПО «Череповецкий государственный университет»

162600 г. Череповец, пр. Луначарского, 5.