Расчет процессов идеального газа

Все многообразие процессов можно разделить на следующие группы: изохорные, изобарные, изотермические, адиабатные, политропные.

p

Рис. 4.2

s

T

T

T

s

p

T

p

s

s

v

v

v

Цель расчета процесса – определение параметров в начальном и конечном состояниях, а также теплоты и работы процесса. Расчет процессов, как правило, сопровождается графическим представлением их в p-v- и T-s- диаграммах (рис. 4.1, рис. 4.2).

Изобары в T-s-диаграмме располагаются эквидистантно между собой
и с увеличением давления смещаются влево; построены на основании уравнения (4.18).

Изохоры в T-s-диаграмме располагаются также эквидистантно между собой и с увеличением объема смещаются вправо; для построения изохор использовалась формула (4.17).

Изотермы в p-v-диаграмме представляют собой симметричные гиперболы, отражающие связь между p и v в изотермическом процессе,

.

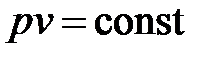(4.28)

Адиабаты (изоэнтропы) в p-v-диаграмме – несимметричные гиперболы, отражающие связь между давлением и объемом в адиабатном обратимом процессе,

,

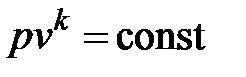(4.29)

располагаются круче изотерм, т. к. показатель адиабаты k >1.

4.2.1. Изобарный процесс

Дано: параметры начального состояния p₁, v₁, удельный объем конечного состояния v₂.

Определить: недостающие термические параметры T₁ и T₂, работу и теплоту процесса (w, l, q).

Изобарный процесс, построенный на основании исходных данных
(p₁, v₁, v₂), в p-v- и T-s-диаграммах представлен на рис. 4.3 и 4.4.

Из уравнения состояния для точки 1 определяется температура T₁:

.

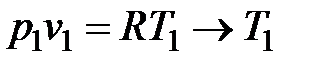Сравнение уравнений состояния для точек 1 и 2 при условии
p₁= p₂ = p = const,

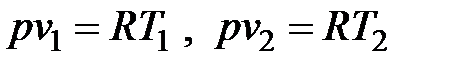
дает связь между v и T в изобарном процессе:

,

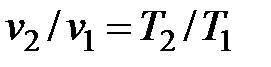(4.30)

из которой можно определить искомую температуру T₂.

Формулы для расчета работы и теплоты изобарного процесса легко получить на основании уравнений

.

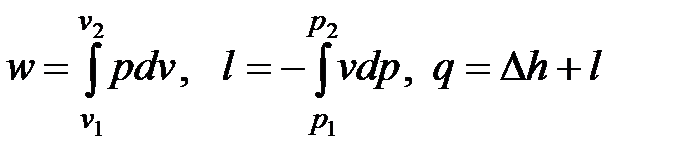Отсюда при p = const имеем

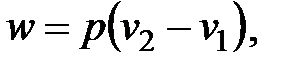	(4.31)
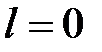,	(4.32)
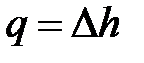.	(4.33)

Работа и теплота изобарного процесса в диаграммах представлены заштрихованными площадями. Работа положительна (w > 0), т. к. v₂ > v₁, теплота подводится (q > 0), поскольку s₂ > s₁.

Из T-s-диаграммы следует: изменение энтальпии (Dh) любого процесса, осуществляемого в интервале температур T₁ – T₂, характеризуется площадью под изобарой в этом интервале температур.

Изохорный процесс

Дано: параметры начального состояния p₁, v₁, давление конечного состояния p₂(p₂ > p₁).

Определить: недостающие термические параметры T₁ и T₂, работу и теплоту процесса (w, l, q).

Изохорный процесс, построенный на основании исходных данных
(p₁, v₁, p₂) в диаграммах p-v и T-s, представлен на рис. 4.5 и 4.6.

Из уравнения состояния для точки 1 определяется температура
T₁ = p₁ • v₁/R. Сравнение уравнений состояния для точек 1 и 2 при условии
v₁ = v₂ = v = const (p₁ •^.v = RT₁, p₂ • v = RT₂) дает связь между давлением и температурой в изохорном процессе:

,

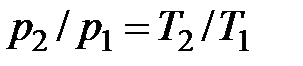(4.34)

из которой можно рассчитать температуру T₂.

Формулы для расчета работы и теплоты изохорного процесса получены на основании уравнений

.

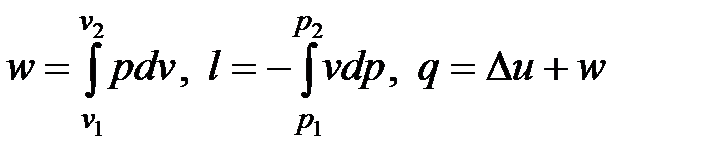При v = const получаем

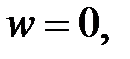	(4.35)
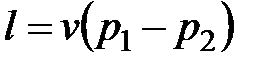,	(4.36)
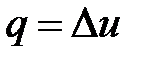.	(4.37)

Работа и теплота изохорного процесса в p-v- и T-s-диаграммах представлена заштрихованными площадями. Работа затрачивается (l < 0), т. к.
p₂ > p₁, теплота подводится (q > 0), поскольку s₂ > s₁.

Из T-s-диаграммы следует: изменение внутренней энергии ( 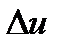) любого процесса, осуществляемого в интервале температур T₁ – T₂, характеризуется площадью под изохорой в этом интервале температур.

Изотермический процесс

Дано: параметры начального состояния p₁, v₁, давление конечного состояния p₂(p₂ > p₁).

Определить: недостающие термические параметры T₁ и v₂, работу и теплоту процесса (w, l, q).

Изотермический процесс, построенный на основании исходных данных (p₁, v₁, p₂) в диаграммах p-v и T-s, представлен на рис. 4.7 и 4.8.

Из уравнения состояния для точки 1 определяется температура
T = p₁• v₁/R. Сравнение уравнений состояния для точек 1 и 2 при условии
T₁ = T₂ = T = const (p₁ • v₁ = RT, p₂ • v₂ = RT) дает связь между давлением и объемом в изотермическом процессе:

,

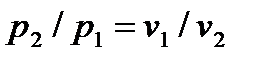(4.38)

из которой можно определить удельный объем v₂.

Формулы для расчета работы и теплоты изотермического процесса получены на основании уравнений

.

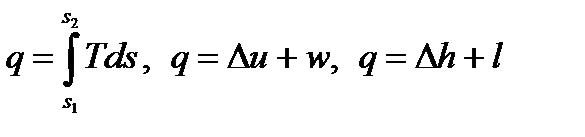Для идеального газа при T = const имеем

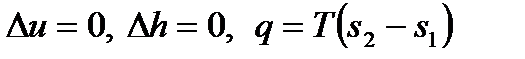,	(4.39)
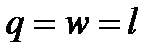,	(4.40)
.

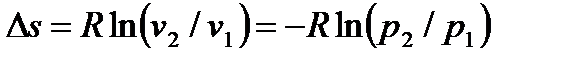Для расчета теплоты (работы) изотермического процесса можно использовать формулы

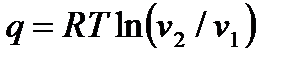,	(4.41)
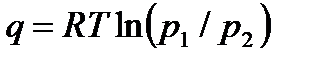.	(4.42)

Работа и теплота изотермического процесса в p-v- и T-s-диаграммах представлена заштрихованными площадями. Равенство работ w и l подтверждается симметрией изотермы относительно осей координат. Работа процесса w < 0, т. к. v₂ < v₁; работа l < 0, поскольку p₂ > p₁; теплота отводится (q < 0), т. к. s₂ < s₁.

Адиабатный процесс

Адиабатным называется процесс, который протекает без теплообмена с окружающей средой (dq = 0).

В обратимых адиабатных процессах энтропия не изменяется (ds = 0,
s = const), в необратимых – энтропия увеличивается (ds > 0).

Уравнение обратимого адиабатного процесса имеет вид

,

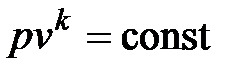(4.43)

где k – показатель адиабаты.

Для идеального газа

.

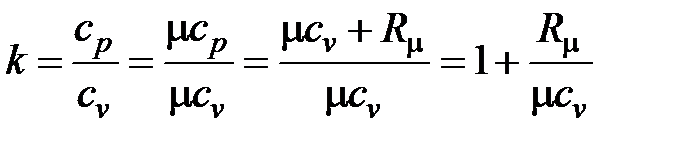(4.44)

Для одноатомного идеального газа показатель адиабаты не зависит от температуры:

.

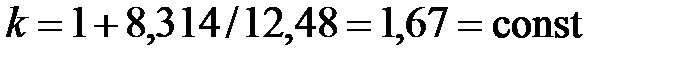Для двух-, трех- и многоатомных идеальных газов k = f(T), т. к. теплоемкость mc_v =f(T). С увеличением температуры показатель адиабаты убывает.

Если принять теплоемкость постоянной в соответствии с молекулярно-кинетической теорией газов, то для двухатомных газов

,

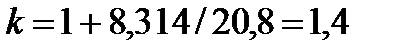для трех- и многоатомных газов:

.

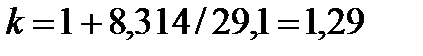Расчет адиабатных процессов двух-, трех- и многоатомных газов при значениях показателя адиабаты 1,4; 1,29 является приближенным, т. к. не учитывает зависимость теплоемкости от температуры.

Совместное решение (4.43) с уравнением состояния идеального газа
pv = RT дает следующие связи параметров:

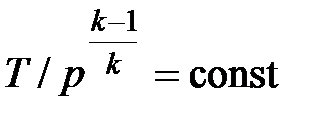,	(4.45)
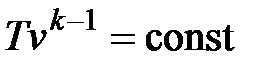.	(4.46)

Для адиабатного процесса 1-2, в котором параметры изменяются от p₁, v₁, T₁ до p₂, v₂, T₂, на основании уравнений (4.43), (4.45), (4.46) можно получить следующие соотношения между параметрами:

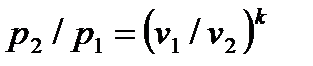,	(4.47)
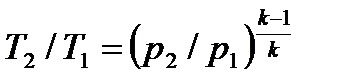,	(4.48)
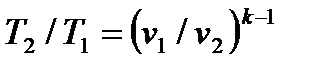.	(4.49)

Совместное решение уравнений

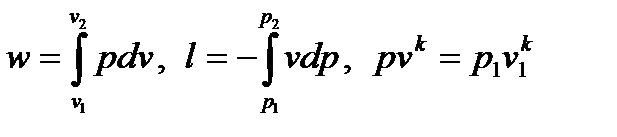
позволяет получить расчетные формулы для работы адиабатного процесса 1-2:

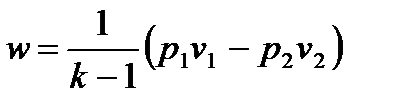,	(4.50)
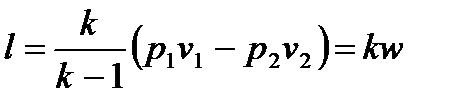.	(4.51)

С учетом уравнения состояния pv = RT, а также соотношения (4.48) формулу (4.50) можно представить следующим образом:

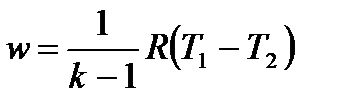,	(4.52)
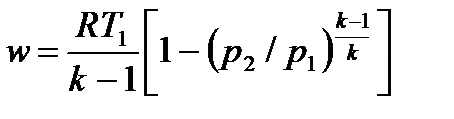.	(4.53)

По формулам (4.46) – (4.53) производят расчеты адиабатных процессов одноатомного идеального газа и приближенные расчеты двух-, трех- и многоатомных газов при значениях k = 1,4; k = 1,29.

Расчет адиабатных процессов с учетом зависимости k = f(T) по вышеприведенным формулам прост, если известны температуры T₁ и T₂. В противном случае используется метод последовательных приближений, что значительно усложняет расчет.

Более простым является табличный метод расчета адиабатного процесса идеального газа с учетом зависимости теплоемкости от температуры. В основе расчета лежат следующие уравнения:

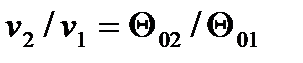,	(4.54)
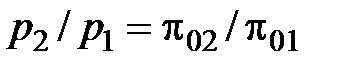,	(4.55)
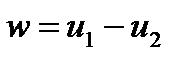,	(4.56)
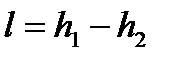.	(4.57)

Здесь 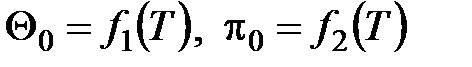– безразмерные величины, приведенные в таблицах термодинамических свойств газов [7]; h, u – табличные значения параметров.

Обратимый адиабатный процесссжатия идеального газа, построенный по исходным параметрам p₁, T₁, p₂ в p-v- и T-s-диаграммах, представлен на рис.4.9 и 4.10.

В p-v-диаграмме адиабата – несимметричная гипербола располагается круче изотермы, в T-s-диаграмме – изоэнтропа (s = const, q = 0).

Необратимые адиабатные процессы (1-2д), протекающие с увеличением энтропии, показаны на рис. 4.11, 4.12.

Работа необратимого адиабатного расширения (см. рис. 4.11) равна

,

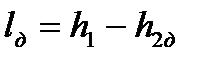и она меньше работы обратимого процесса, вычисляемого по формуле

.

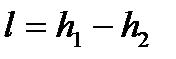Напротив, работа необратимого адиабатного сжатия (см. рис. 4.12), равная

,

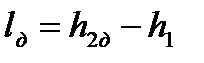больше работы обратимого процесса

.

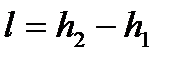Политропные процессы

Политропные процессы описываются уравнением

,

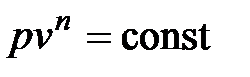(4.58)

где n – показатель политропы, который не зависит от температуры (n = const) и изменяется в пределах от -µ до µ.

Внешняя схожесть уравнений (4.43) и (4.58) позволяет записать расчетные формулы политропного процесса, аналогичные адиабатному:

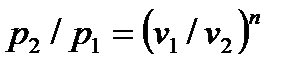,	(4.59)
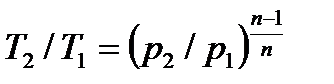,	(4.60)
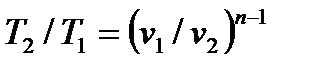,	(4.61)
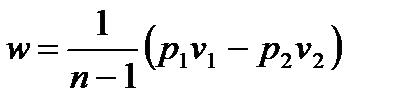,	(4.62)
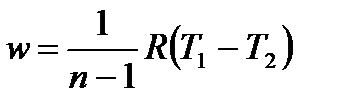,	(4.63)
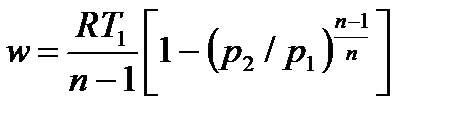,	(4.64)
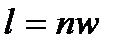.	(4.65)

Теплота политропного процесса рассчитывается по уравнению

,

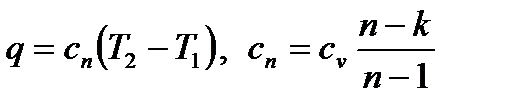(4.66)

где c_п– теплоемкость политропного процесса.

Все многообразие процессов можно описать политропой с показателем µ < n < µ. Изохорный, изобарный, изотермический, адиабатный процессы являются частным случаем политропных процессов с определенным показателем n. Подставляя конкретные его значения в формулы (4.58) и (4.66), можно доказать, что при

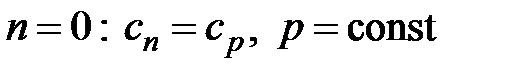- процесс изобарный;

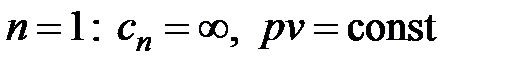- процесс изотермический;

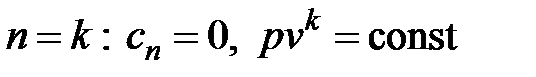- процесс адиабатный;

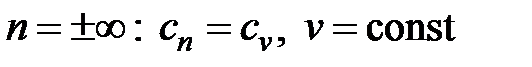- процесс изохорный.

На рис. 4.13 и 4.14 в p-v- и T-s-диаграммах представлено все множество политропных процессов с показателем n, изменяющиxся от -µ до µ.

Можно выделить следующие группы процессов:

1. Процессы расширения (dv > 0, dw > 0) – области 1, 2, 3, 4.

2. Процессы сжатия (dv < 0, dw < 0) – области 5, 6, 7, 8.

3. Процессы подвода теплоты (ds > 0, dq > 0) – области 8, 1, 2, 3.

4. Процессы отвода теплоты (ds < 0, dq < 0) – области 4, 5, 6, 7.

5. Процессы, протекающие с увеличением температуры (dT > 0, du > 0, dh > 0) – области 7, 8, 1, 2.

6. Процессы, протекающие с уменьшением температуры (dT < 0, du < 0, dh <0) – области 3, 4, 5, 6.

7. Процессы с отрицательной теплоемкостью (c_n < 0, 1 < n < k) – области 3, 7.

В области 3 при подводе теплоты (dq > 0) температура, внутренняя энергия, энтальпия уменьшаются (dT < 0, du < 0, dh < 0). В области 7 при отводе теплоты (dq < 0) температура, внутренняя энергия, энтальпия увеличиваются (dT > 0, du > 0, dh > 0). Это может быть только при отрицательной теплоемкости. В процессах с отрицательной теплоемкостью 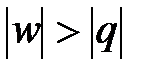, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела, а затрачиваемая работа на сжатие компенсирует не только отводимую теплоту, но и повышает внутреннюю энергию рабочего тела.

При изображении политропных процессов в диаграммах p-v и T-s необходимо определить область, к которой они принадлежат, путем сравнения показателя политропы с n = k, n =1 и т. д.

Политропный процесс газа с показателем 1<n<k, построенный по исходным параметрам p₁, t₁, p₂ (p₂ > p₁) в p-v- и T-s-диаграммах, представлен на
рис. 4.15 и 4.16.

В p-v-диаграмме политропа – несимметричная гипербола, которая располагается круче изотермы, т. к. n >1.

В T-s-диаграмме политропа – логарифмическая кривая, которая располагается между изотермой и изоэнтропой, т. к. 1< n < k.

14) Влажный воздух и его процессы

Итак, смесь сухого воздуха и водяного пара называется влажным воздухом. Именно влажный воздух окружает нас повсеместно, именно он сушит бельё после стирки, постепенно опустошает ёмкость с водой, а иногда напоминает о себе запотевшими стеклами и конденсатом на поверхности холодного предмета. Он может способствовать накоплению статического электричества на металлических поверхностях, развитию астмы у людей, иссушать растения, ухудшать наше самочувствие в теплую погоду. Попробуем же разобраться с его свойствами, характеристиками и процессами! Перед нами - влажный воздух!

Влажный воздух, как мы уже определились, это смесь сухого воздуха с водяным паром, причем смесь эта не находится в состоянии равновесия, т.е. постоянно меняется, и именно эта неравновесность представляет огромную сложность в изучении. Без неё книги о влажном воздухе превратились бы в пару абзацев.

Как и у любого вещества, у влажного воздуха есть основные параметры, определяющие его состояние, и достаточно трех независимых из них, чтобы полностью определить его состояние. Однако, из-за сложности ввиду неравновесности, а также для удобства описания процессов обычно выделяют 6 основных параметров влажного воздуха. Перечислим их: