Примеры решения нелинейных уравнений
Теоретические сведения
Пускай 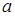 ‑ некоторое приближенное значение точного числа
‑ некоторое приближенное значение точного числа 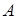 .
.
Если 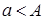 , то
, то 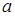 приближает
приближает 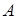 с недостатком.
с недостатком.
Если 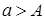 , то
, то 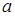 приближает
приближает 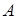 с избытком.
с избытком.
Под абсолютной погрешностью 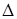 приближенного числа
приближенного числа 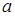 понимают абсолютное значение разницы точного и приближенного значений
понимают абсолютное значение разницы точного и приближенного значений
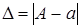 | (1.1) |
Под относительной погрешностью 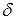 приближеннго числа
приближеннго числа 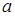 понимают отношение абсолютной погрешности к модулю точного значения числа. Часто относительная погрешность измеряется процентами точного значения
понимают отношение абсолютной погрешности к модулю точного значения числа. Часто относительная погрешность измеряется процентами точного значения
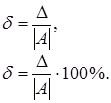 | (1.2) |
Известно, что любое число может быть представлено в форме десятичной дроби, конечной или бесконечной.
Приближенные десятичные числа выражаются лишь конечными десятичными дробями.
Говорят, что n первых значащих цифр десятичного числа точные, если абсолютная погрешность этого числа не превышает половину единицы разряда, выражющего n-ю значащую цифру, считая слева направо, то есть если
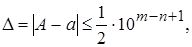 | (1.3) |
то 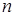 цифр точные.
цифр точные.
При проведении расчетов с приближенными числами следует руководствоваться следующими правилами:
1. При сложении и вычитании приближенных чисел в результате должны сохраняться столько точных разрядов, сколько их в наименьшем из слагаемых.
2. Правило 1 имеет место в случае операций умножения и деления.
3. В случае операции возведения в степень следует сохранять столько значащих цифр, сколько их имеет основание степени.
4. Правило 3 имеет место для операции извлечения корня.
5. Во всех промежуточных результатах расчетов следует брать на одну – две цифры больше. В окончательных результатах они отбрасываются.
6. Если данные можно брать с произвольной точностью, то для получения результата с 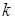 верными цифрами исходные данные следует брать с таким количеством точных цифр, чтобы получить
верными цифрами исходные данные следует брать с таким количеством точных цифр, чтобы получить  точную цифру в результате.
точную цифру в результате.
Примеры
Пример 1.1.
Число 402,35 имеет абсолютную погрешность 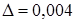 .
.
Очевидно, 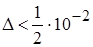 . Все цифры этого числа точные.
. Все цифры этого числа точные.
Пример 1.2. Округлить следующие числа до четырех значащих цифр, определить абсолютную 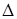 и относительную
и относительную 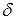 погрешности полученных приближенных чисел А1=625,51; А2=0,0039227.
погрешности полученных приближенных чисел А1=625,51; А2=0,0039227.
Решение
а1=625,5;
а2=0,003923;
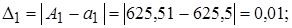
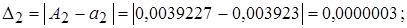
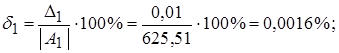
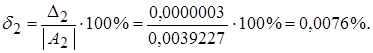
Пример 1.3. Определить абсолютную погрешность приближенного числа по его относительной погрешности а=20,725, 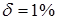 .
.
Решение
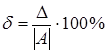 ;
;  ;
;
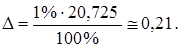
Пример 1.4. Определить количество точных знаков чисел а1 и а2, если известны их абсолютные погрешности 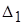 и
и 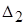 :
:
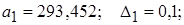
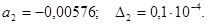
Решение
а1 имеет три точные значащие цифры
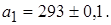
а2 имеет две точные значащие цифры, поскольку
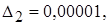
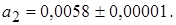
Пример 1.5. Определить количество точных знаков числа а, если известна его относительная погрешность 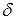 :
:
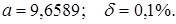
Решение
Находим 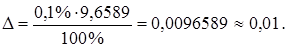
Поэтому, а имеет две точных цифры
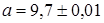 .
.
Пример 1.6. Даны числа 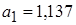 и
и 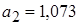 с абсолютными погрешностями
с абсолютными погрешностями 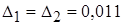 . Оценить относительную погрешность их разности
. Оценить относительную погрешность их разности 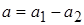 .
.
Решение
а=1,137-1,073=0,064;
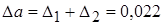 ;
;
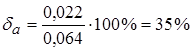 ;
;
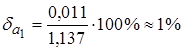 ;
;
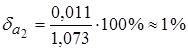 .
.
Таким образом, относительная погрешность разности в 35 раз больше относительных погрешностей исходных данных. Результат не имеет ни одной точной цифры.
Пример 1.7. Вычислить 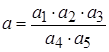 , считая, что все числа даны с точными знаками:
, считая, что все числа даны с точными знаками:
а1=3,2; а2=356,7; а3=0,04811; а4=7,1948; а5=34,56.
Решение
Наибольшую относительную погрешность имеет число а1=3,2:
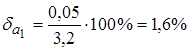 .
.
Поэтому относительная погрешность результата составит также приблизительно 1,6%, то есть результат будет содержать две точные цифры.
Сохраним в исходных данных по три точных цифры (один запасной знак), получим
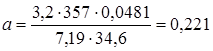 .
.
Абсолютную погрешность результата вычислим по его относительной погрешности
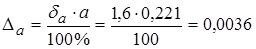 .
.
Округляем результат, отбрасывая запасной знак, получим а=0,22 с абсолютной погрешностью 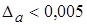 .
.
Пример 1.8. Найти сумму приближенных чисел 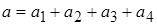 :
:
а1=0,146; а2=321,5; а3=78,27; а4=39,1.
Все данные знаки точные.
Решение
Наибольшую абсолютную погрешность имеют числа а2=321,5 и а4=39,1. Поэтому можно считать, что абсолютная погрешность суммы составляет 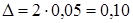 .
.
Округляем слагаемые по примеру а2 и а4, сохраняем один запасной разряд
а=0,15+321,5+78,27+39,1=439,02.
В окончательном результате запасной знак отбрасываем, получим
а=439,0.
К абсолютной погрешности 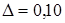 прибавим погрешность округления
прибавим погрешность округления 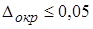 . Тогда
. Тогда
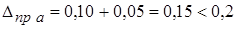 .
.
Таким образом, 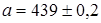 .
.
Индивидуальные задания к лабораторной работе№1
1. Округлить числа А1, А2, А3 до четырех значащих цифр, определить абсолютные и относительные погрешности полученных приближенных чисел:
| Варіант | А1 | А2 | А3 |
| 22,5538 | 2,855 | 0,002836 | |
| 17,2834 | 17,283 | 0,0017215 | |
| 34,8341 | 6,426 | 0,006401 | |
| 10,8495 | 34,834 | 0,0034821 | |
| 24,5643 | 2,345 | 0,002339 | |
| 13,6253 | 10,844 | 0,0010799 | |
| 15,8071 | 8,241 | 0,008311 | |
| 24,3608 | 23,574 | 0,0023611 | |
| 83,7306 | 7,521 | 0,007511 | |
| 12,6095 | 27,156 | 0,0027133 | |
| 46,0453 | 15,873 | 0,0015865 | |
| 15,6044 | 1,543 | 0,001539 | |
| 32,7486 | 4,884 | 0,004881 | |
| 38,4258 | 35,711 | 0,0035721 | |
| 15,8405 | 5,843 | 0,0005825 |
2. Определить абсолютные погрешности чисел а1 и а2 по известным относительным погрешностям δ1и δ2:
| Вариант | a1 | 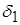 , % , % | a2 | 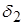 , % , % |
| 232,44 | 0,896 | |||
| 35,72 | 0,7 | 0,453 | ||
| 81,05 | 0,2 | 0,012 | ||
| 142,31 | 0,001 | 0,01 | ||
| 274,12 | 0,018 | 0,9 | ||
| 52,35 | 0,05 | 0,125 | ||
| 45,08 | 0,508 | |||
| 23,75 | 0,911 | |||
| 91,11 | 0,381 | |||
| 11,91 | 0,3 | 0,397 | ||
| 253,02 | 0,9 | 0,856 | 0,3 | |
| 311,45 | 0,231 | |||
| 76,62 | 0,052 | |||
| 32,51 | 0,086 | 0,7 | ||
| 199,99 | 0,2 | 0,111 | 0,1 |
3. Определить количество точных знаков чисел а1 и а2, если известны их абсолютные погрешности Δ1 и Δ2:
| Вариант | a1 | 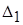 | a2 | 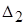 |
| 0.3941 | 0.25  10-2 10-2 | -0.12356 | 0.36  10-3 10-3 | |
| 0.1132 | 0.1  10-3 10-3 | -2.4543 | 0.32  10-2 10-2 | |
| 38.2543 | 0.27  10-2 10-2 | -8.3445 | 0.22  10-2 10-2 | |
| 293.481 | 0.1 | -3.7834 | 0.41  10-2 10-2 | |
| 2.325 | 0.1  10-1 10-1 | -13.537 | 0.005 | |
| 14.00231 | 0.1  10-3 10-3 | -13.6253 | 0.2 | |
| 0.0842 | 0.15  10-2 10-2 | -1.784 | 0.6  10-2 10-2 | |
| 0.00381 | 0.1  10-4 10-4 | -3.6878 | 0.1  10-2 10-2 | |
| 32.285 | 0.2  10-2 10-2 | -27.1548 | 0.2  10-3 10-3 | |
| 0.2113 | 0.5  10-2 10-2 | -0.8467 | 0.4  10-3 10-3 | |
| 22.553 | 0.16  10-1 10-1 | -0.98351 | 0.3  10-3 10-3 | |
| 6.4257 | 0.24  10-2 10-2 | -5.6483 | 0.8  10-2 10-2 | |
| 0.5748 | 0.34  10-2 10-2 | -32.7486 | 0.12  10-2 10-2 | |
| 2.3485 | 0.42  10-2 10-2 | -4.88445 | 0.5  10-3 10-3 | |
| 5.435 | 0.28  10-2 10-2 | -38.4258 | 0.14  10-2 10-2 |
4. Определить количество точных знаков числа а, если известна его относительная погрешность 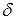 :
:
| Вариант | A | 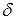 , % , % |
| 3.87683 | 0.33 | |
| 0,088748 | 0,56 | |
| 23,75642 | 1,5 | |
| 72,354 | ||
| 46,7843 | 0,5 | |
| 24,3872 | ||
| 45,7832 | ||
| 8,24163 | 0,66 | |
| 8,25163 | 0,6 | |
| 0,3567 | 0,01 | |
| 0,85637 | ||
| 0,3945 | 0,15 | |
| 3,7542 | 0,8 | |
| 2,8867 | 0,04 | |
| 0,66385 | 0,001 |
5. Даны числа 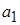 и
и 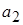 . Все данные цифры этих чисел точные. Оцените относительную погрешность их разности
. Все данные цифры этих чисел точные. Оцените относительную погрешность их разности 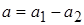 . Оцените потерю точности результата по сравнению с исходными данными.
. Оцените потерю точности результата по сравнению с исходными данными.
| Вариант | a1 | a2 |
| 2.855 | 2.836 | |
| 17.283 | 17.215 | |
| 6.426 | 6.401 | |
| 34.834 | 34.820 | |
| 2.345 | 2.339 | |
| 10.844 | 10.799 | |
| 8.241 | 8.300 | |
| 23.574 | 23.600 | |
| 7.521 | 7.506 | |
| 27.156 | 27.133 | |
| 15.873 | 15.865 | |
| 1.543 | 1.539 | |
| 4.884 | 4.880 | |
| 35.711 | 35.721 | |
| 5.843 | 5.825 |
6. Вычислить 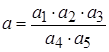 , считая, что все числа даны точными знаками. Оцените абсолютную и относительныю погрешности результата.
, считая, что все числа даны точными знаками. Оцените абсолютную и относительныю погрешности результата.
| Вариант | a1 | a2 | a3 | a4 | a5 |
| 8,5 | 215,14 | 0,00975 | 9,375 | 17,81 | |
| 1,6 | 161,52 | 0,03611 | 11,562 | 45,32 | |
| 2,3 | 120,41 | 0,02972 | 30,12 | ||
| 1,2 | 122,57 | 0,01176 | 12,265 | 28,35 | |
| 3,8 | 152,81 | 0,03521 | 7,399 | 39,26 | |
| 6,9 | 392,85 | 0,02352 | 14,008 | 28,75 | |
| 7,2 | 411,12 | 0,01095 | 5,792 | 48,32 | |
| 1,5 | 392,24 | 0,00859 | 9,293 | 20,15 | |
| 3,2 | 225,55 | 0,02151 | 7,411 | 19,91 | |
| 5,8 | 109,53 | 0,01615 | 11,759 | 31,11 | |
| 6,1 | 235,21 | 0,00796 | 6,831 | 18,15 | |
| 2,4 | 352,12 | 0,01204 | 8,923 | 42,77 | |
| 2,7 | 117,59 | 0,1528 | 10,118 | 25,14 | |
| 5,6 | 297,17 | 0,00998 | 12,381 | 19,12 | |
| 4,7 | 361,12 | 0,03927 | 8,442 | 29,10 |
7. Найдите сумму приближенных чисел 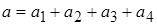 . Все данные знаки точные. Оцените абсолютную погрешность результата.
. Все данные знаки точные. Оцените абсолютную погрешность результата.
| Вариант | a1 | a2 | a3 | a4 | a5 |
| 0,14532 | 211,63 | -61,95 | 0,007293 | 3,485 | |
| 0,41512 | 317,92 | -21,83 | 0,00899 | 11,753 | |
| 0,52161 | 157,11 | -41,52 | 0,008251 | 4,884 | |
| 0,14021 | 212,54 | -76,24 | 0,004021 | 3,451 | |
| 0,35221 | 125,32 | -51,81 | 0,000697 | 0,785 | |
| 0,58293 | 455,22 | -29,01 | 0,001512 | 12,570 | |
| 0,21114 | 421,93 | -51,20 | 0,000158 | 4,753 | |
| 0,42293 | 211,14 | -23,04 | 0,001901 | 14,285 | |
| 0,55522 | 500,93 | -57,82 | 0,002532 | 4,308 | |
| 0,35901 | 182,51 | -62,93 | 0,001253 | 5,200 | |
| 0,12532 | 109,92 | -53,82 | 0,006711 | 12,384 | |
| 0,21053 | 140,21 | -21,03 | 0,002792 | 6,204 | |
| 0,95901 | 251,61 | -23,54 | 0,001163 | 13,827 | |
| 0,70792 | 410,06 | -18,17 | 0,000179 | 5,408 | |
| 0,21454 | 415,93 | -71,23 | 0,006568 | 4,653 |
Лабораторная работа №2
Простейшие вычисления и операции в MATHCAD
Порядок выполнения работы
I. Вычислить значения арифметических выражений 25+ 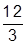 и 25+
и 25+ 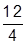 .
.
| Указания. | Отображение на экране: |
| 1. Щелкните мышью по любому месту в рабочем документе - в поле появится крестик, обозначающий позицию, с которой начинается ввод. |  |
| 2. Введите с клавиатуры символы в следующей последовательности: 25+12/3. | 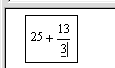 |
| 3. Введите с клавиатуры знак равенства, нажав клавишу <=>. Mathcad вычисляет значение выражения и выводит справа от знака равенства результат. |  |
| 4. Щелкните мышью справа внизу возле цифры 3 и нажмите клавишу <Backspace> (справа во втором ряду клавиатуры). Теперь значение выражения не определено, место ввода помечено черной меткой и ограничено угловой рамкой. | 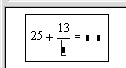 |
| 5. Введите с клавиатуры цифру 4 и щелкните мышью вне выделяющей рамки. | 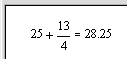 |
6. Теперь удалим выражение с экрана. Щелкните мышью по любому месту в выражении 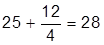 |  |
| 7. Нажимайте клавишу <Space> до тех пор, пока все выражение не будет выделено угловой синей рамкой. |  |
| 8. Нажмите клавишу <Backspace> (поле ввода окрасится в черный цвет) и, нажав клавишу <Del>, удалите выделенное. Выражение исчезнет с экрана. |  |
II. Вычислить значение выражения, содержащего переменные:
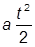 при t = 5, а = 9.8.
при t = 5, а = 9.8.
| Указания: | Отображение на экране: |
| 1. Щелкните мышью по свободному месту в рабочем документе и введите с клавиатуры символы а :*. |  |
| 2. Введите с клавиатуры символы 9 . 8 и щелкните по свободному месту вне поля ввода. |  |
| 3. Щелкните мышью по свободному месту в рабочем документе и введите с клавиатуры t : 5, щелкните по свободному месту вне поля ввода. | 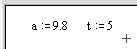 |
| 4. Щелкните мышью по свободному месту в рабочем документе и введите с клавиатуры а * t^2 <Space> / 2 <Space> <Space> = и щелкните по свободному месту вне поля ввода. | 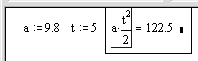 |
Если при вводе выражения была допущена ошибка, выделите неправильный символ угловой рамкой (щелкните мышью справа внизу возле символа), удалите выделенный символ (нажмите клавишу <Backspace>) и введите в помеченной позиции исправление.
Mathcad читает и выполняет введенные выражения слева направо и сверху вниз, поэтому следите, чтобы выражение для вычисления располагалось правее или ниже определенных для него значений переменных.
III. Определить функцию f(x) = 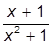 , вычислить ее значение при х =1.2 и построить таблицу значений функции для х Î [0, 10] с шагом 1.
, вычислить ее значение при х =1.2 и построить таблицу значений функции для х Î [0, 10] с шагом 1.
| Указания: | Отображение на экране: |
| 1. Щелкните по свободному месту в рабочем документе, введите с клавиатуры f ( х ) = х + 1 <Space> / х ^ 2 <Space> + 1 и затем щелкните по рабочему документу вне поля ввода. | 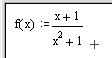 |
2. Щелкните по свободному месту в рабочем документе и введите с клавиатуры  f(1.2)=. Сразу после ввода знака равенства немедленно выводится вычисленное значение функции f(x) при х = 1.2. f(1.2)=. Сразу после ввода знака равенства немедленно выводится вычисленное значение функции f(x) при х = 1.2. |  |
| 3. Задать дискретные значения аргумента х Î [0, 10] с шагом 1: щелкнув по свободному месту в рабочем документе, введите с клавиатуры х : 0 , 1 ; 10 и щелкните вне поля ввода. |  |
| 4. Щелкнув по свободному месту в рабочем документе, введите с клавиатуры f(x)=. В результате под именем функции появится таблица значений функции. |  |
IV. Построить график функции f{t) = 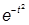 .
.
| Указания: | Отображение на экране: |
| 1. Щелкните по свободному месту в рабочем документе и введите с клавиатуры f( t ):е х р (- t^2 <Space> ) и щелкните мышью вне поля ввода. |  |
2. Щелкните по свободному месту в рабочем документе, затем - по кнопке  в панели математических инструментов и в открывшейся панели щелкните по кнопке . в панели математических инструментов и в открывшейся панели щелкните по кнопке .  . . |  |
| 3. Курсор установлен в помеченной позиции возле оси абсцисс. Введите с клавиатуры имя аргумента t, затем щелкните по помеченной позиции возле оси ординат, введите с клавиатуры f(t) и щелкните вне прямоугольной рамки. | 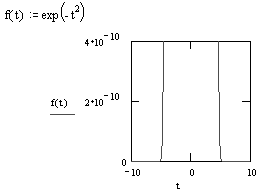 |
| 4. График получился невыразительным. Нужно определить промежуток изменения аргумента равным [—2, 2]. Для этого щелкните по полю графика, затем — по числу, задающему наименьшее значение аргумента (число в левом нижнем углу ограниченного рамкой поля графиков), нажмите на клавишу <Backspace> и введите с клавиатуры ”–2”. Аналогично измените вторую границу — вместо числа в правом нижнем углу поля графика введите 2. Щелкните мышью вне поля графика. | 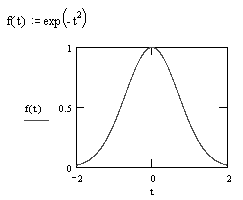 |
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Индивидуальные задания к лабораторной работе №2
I. Вычислить значения арифметических выражений:
| 1. | 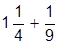 | 11. | 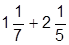 | |
| 2. | 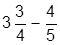 | 12. | 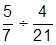 | |
| 3. | 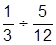 | 13. | 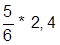 | |
| 4. | 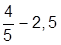 | 14. | 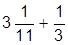 | |
| 5. | 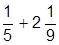 | 15. | 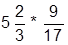 | |
| 6. | 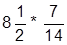 | 16. | 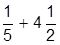 | |
| 7. | 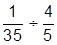 | 17. | 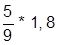 | |
| 8. | 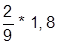 | 18. | 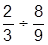 | |
| 9. | 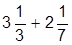 | 19. | 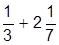 | |
| 10. | 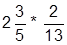 | 20. | 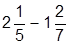 |
II. Вычислить значение выражения:
| 1. | 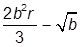 , при , при 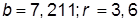 | 11. | 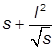 , при , при 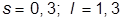 | |
| 2. | 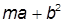 , при , при 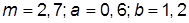 | 12. | 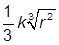 , при , при 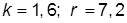 | |
| 3. | 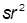 , при , при 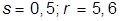 | 13. | 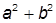 , при , при 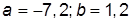 | |
| 4. | 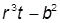 , при , при 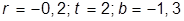 | 14. | 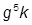 , при , при 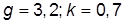 | |
| 5. | 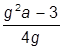 , при , при 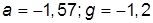 | 15. | 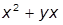 , при , при 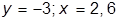 | |
| 6. | 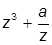 , при , при 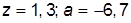 | 16. | 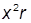 , при , при 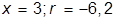 | |
| 7. | 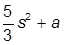 , при , при 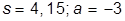 | 17. | 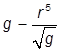 , при , при 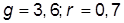 | |
| 8. | 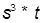 , при , при 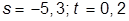 | 18. | 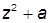 , при , при 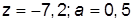 | |
| 9. | 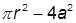 , при , при 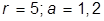 | 19. | 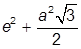 , при , при 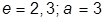 | |
| 10. | 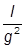 , при , при 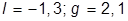 | 20. | 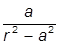 , при , при 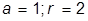 |
III. Определить функцию f(x), вычислить ее значение при x=2,9 и построить таблицу значений функции для xО[2;12] с шагом 1. Построить график функции.
| 1. | 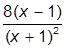 | 11. | 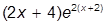 | |
| 2. | 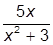 | 12. | 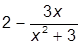 | |
| 3. | 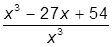 | 13. | 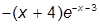 | |
| 4. | 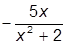 | 14. | 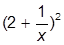 | |
| 5. | 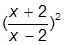 | 15. | 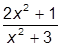 | |
| 6. | 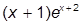 | 16. | 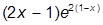 | |
| 7. | 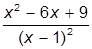 | 17. | 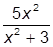 | |
| 8. | 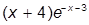 | 18. | 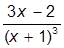 | |
| 9. | 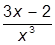 | 19. | 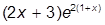 | |
| 10. | 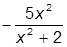 | 20. | 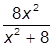 |
Лабораторная работа №3
Численные методы решение нелинейных уравнений
Наиболее распространенными методами уточнения корней являются следующие: графического решения, деления пополам, хорд, касательных (Ньютона), комбинированный (хорд и касательных), итераций.
Все возможные случаи при уточнении корней можно классифицировать с помощью таблицы 3.1.
Таблица 3.1
| № вар. | СХЕМА | 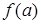 | 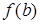 | 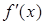 | 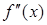 | Нулевое приближение  | |
| метод хорд | метод касательных | ||||||
| I | 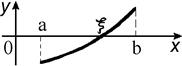 | ‑ | + | + | + |  | 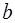 |
| II | 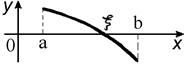 | + | ‑ | ‑ | ‑ | 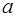 | 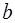 |
| III | 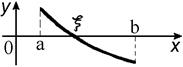 | + | ‑ | ‑ | + |  |  |
| IV |  | ‑ | + | + | ‑ |  | 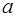 |
Дано уравнения 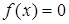 , где
, где 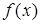 ‑ непрерывная функция, которая имеет в интервале
‑ непрерывная функция, которая имеет в интервале 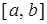 непрерывные и знакопостоянные производные первого и второго порядков. Корень
непрерывные и знакопостоянные производные первого и второго порядков. Корень 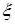 изолирован и отделен на
изолирован и отделен на 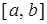 , то есть выполняется условие
, то есть выполняется условие 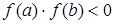 . Необходимо уточнить корень
. Необходимо уточнить корень 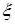 с заданной степенью точности
с заданной степенью точности 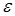 .
.
Рассмотрим некоторые из перечисленных выше методов.
Метод хорд
Идея метода хорд состоит в том, что на достаточно малом промежутке 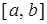 дуга кривой
дуга кривой 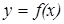 заменяется стягивающей ее хордой. Искомый корень уравнения
заменяется стягивающей ее хордой. Искомый корень уравнения 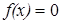 есть абсцисса точки пересечения графика функции
есть абсцисса точки пересечения графика функции 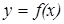 с осью Ох.
с осью Ох.
1. Если имеют место варианты I и II, тогда 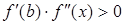 на отрезке
на отрезке 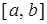 , то приближенные значения корней
, то приближенные значения корней 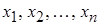 будут находиться внутри отрезков
будут находиться внутри отрезков 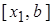 ,
, 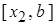 , …, то есть недвижимым концом отрезка
, …, то есть недвижимым концом отрезка 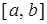 будет конец
будет конец 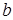 , а приближенные значения корней будут находиться по формуле
, а приближенные значения корней будут находиться по формуле
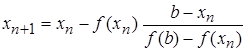 , , | (3.1) |
при этом 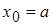
2. Если имеют место варианты III и IV, тогда 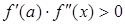 на отрезке
на отрезке 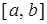 , то приближенные значения
, то приближенные значения 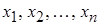 корней будут находиться внутри отрезков
корней будут находиться внутри отрезков 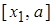 ,
, 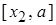 , …, то есть недвижимым концом отрезка
, …, то есть недвижимым концом отрезка 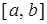 будет конец
будет конец 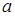 , а приближенные значения корней будут находиться по формуле
, а приближенные значения корней будут находиться по формуле
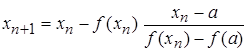 , , | (3.2) |
при этом 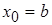
Выбор тех или других формул можно осуществить, пользуясь простым правилом: недвижимым концом отрезка является тот, для которого знак функции совпадает со знаком второй производной, а нулевое приближение 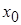 выбирается согласно условия
выбирается согласно условия
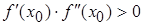 . . | (3.3) |
Процесс последовательного приближения к корню нужно продолжать до тех пор, пока не будет выполнено условие 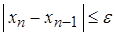 , где
, где 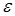 ‑ заданная точность;
‑ заданная точность; 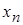 и
и 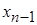 - приближения, полученные на
- приближения, полученные на 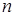 -м и
-м и 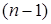 -м шагах. При этом уточненное значение корня принимается
-м шагах. При этом уточненное значение корня принимается 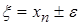 .
.
Метод Ньютона (метод касательных)
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой 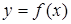 касательной, проведенной к некоторой точке кривой. Точка пересечения этой касательной с осью абсцисс дает нам первое приближение
касательной, проведенной к некоторой точке кривой. Точка пересечения этой касательной с осью абсцисс дает нам первое приближение 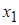 корня
корня 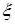 .
.
Любое 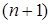 -ое приближение корня определяется равенством
-ое приближение корня определяется равенством
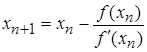 . . | (3.4) |
Выбор нулевого приближения корня 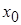 осуществляется таким образом:
осуществляется таким образом:
если 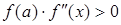 на
на 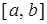 , то
, то 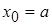 ;
;
если 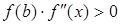 на
на 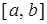 , то
, то 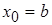 .
.
Чем большее численное значение производной 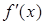 в окрестности данного корня, тем меньшая поправка, которую необходимо учитывать в
в окрестности данного корня, тем меньшая поправка, которую необходимо учитывать в 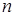 -м приближении. Поэтому метод Ньютона особенно удобно применять тогда, когда в окрестности данного корня график функции имеет большую крутизну.
-м приближении. Поэтому метод Ньютона особенно удобно применять тогда, когда в окрестности данного корня график функции имеет большую крутизну.
Если численное значение производной возле корня мало, то поправки будут большими и процесс уточнения корня может оказаться продолжительным. Если кривая близ точки сечения с осью Ох почти горизонтальная, то применять метод Ньютона не рекомендуется.
Точность приближения на 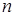 -м шагу оценивается таким образом:
-м шагу оценивается таким образом:
если 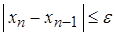 , то
, то 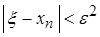 .
.
Если производная 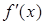 мало меняется на отрезке
мало меняется на отрезке 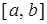 , то для упрощения вычислений можно использовать формулу
, то для упрощения вычислений можно использовать формулу
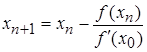 , , | (3.5) |
то есть значение производной в начальной точке достаточно вычислить один раз.
Метод итераций или метод последовательных приближений
Для применения метода итераций (латинское "итерацио" ‑ повторение) исходное уравнение 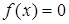 (
( 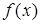 ‑ непрерывная функция) необходимо, во-первых, записать его в виде
‑ непрерывная функция) необходимо, во-первых, записать его в виде 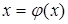 , во-вторых, выделить интервал
, во-вторых, выделить интервал 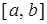 изоляции корня этого уравнение и в-третьих, выбрать нулевое приближение корня
изоляции корня этого уравнение и в-третьих, выбрать нулевое приближение корня 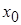 . Для получения первого приближения
. Для получения первого приближения 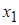 в правую часть уравнения
в правую часть уравнения 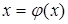 вместо
вместо 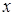 подставляем
подставляем 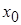 , так что
, так что 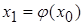 .
.
Следующие приближения образовываются по схеме
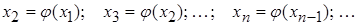 | (3.6) |
Таким образом, в результате применения некоторого одинакового процесса строятся последовательные приближения
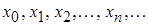
При этом могут быть два случая:
1) процесс может сходиться, то есть последовательные приближения направляются к некоторой конечной границе 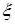 , которая является корнем уравнения;
, которая является корнем уравнения;
2) процесс может расходиться, то есть конечной границы построенных приближений существовать не будет; из этого не вытекает, что решения исходного уравнения не существует, просто могло оказаться, что процесс последовательных приближений избран неудачно.
Приближение 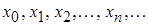 нужно вычислять до тех пор, пока не будет выполнено неравенство
нужно вычислять до тех пор, пока не будет выполнено неравенство
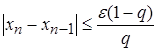 ,
,
где 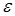 ‑ заданная предельная абсолютная погрешность корня
‑ заданная предельная абсолютная погрешность корня 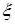 .
.
Если 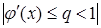 и
и 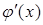 положительная вокруг корня, то последовательные приближения
положительная вокруг корня, то последовательные приближения 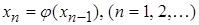 и
и 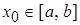 сходятся к корню монотонно. Если же производная
сходятся к корню монотонно. Если же производная 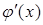 отрицательная, то последовательные приближения колеблются возле корня
отрицательная, то последовательные приближения колеблются возле корня 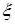 .
.
Примеры решения нелинейных уравнений
Пример 3.1.
Найти корень уравнения 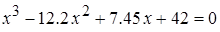 на отрезке [10, 12] методом хорд.
на отрезке [10, 12] методом хорд.
Решение
Вычисляем значение функции на концах отрезка: 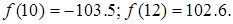
Поскольку 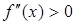 , то за нулевое приближение принимаем
, то за нулевое приближение принимаем 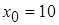 и вычисление будем проводить по формуле (3.2).
и вычисление будем проводить по формуле (3.2).
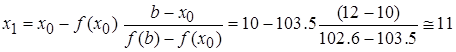 .
.
Итак, 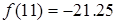 . Это говорит о том, что истинный корень расположен в интервале [11, 12].
. Это говорит о том, что истинный корень расположен в интервале [11, 12].
Повторяя процесс для определения второго приближения корня, получим 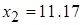 , для которого значения функции
, для которого значения функции 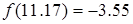 . Теперь корень находится в интервале [11.17, 12]. В конце концов, третье приближение дает нам
. Теперь корень находится в интервале [11.17, 12]. В конце концов, третье приближение дает нам 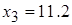 , для которого
, для которого 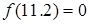 .
.
Таким образом, 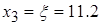 , то есть в данном примере на третьем шаге мы получили точное значение корня.
, то есть в данном примере на третьем шаге мы получили точное значение корня.
Пример 3.2. Методом касательных уточнить корень 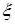 уравнения
уравнения 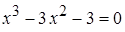 для
для 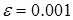 , расположенный на отрезке [-2.75, -2.5].
, расположенный на отрезке [-2.75, -2.5].
Решение
По условию 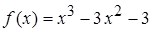 . Определяем вторую производную
. Определяем вторую производную 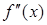 :
:
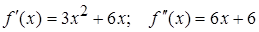 .
.
Таким образом, 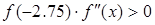 , поэтому
, поэтому 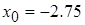 .
.
Определяем значение первой производной в точке 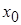 :
:
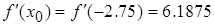 .
.
Для удобства дальнейшие вычисления сводим в таблицу 3.2.
Таблица 3.2
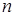 | 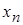 | 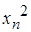 | 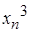 | 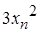 | 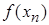 | 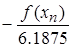 |
| -2.75 | -20.797 | 7.5625 | 22.6875 | -1.111 | 0.179 | |
| -2.571 | -16.994 | 6.6100 | 19.8300 | -0.164 | 0.026 | |
| -2.545 | -16.484 | 6.4770 | 19.431 | -0.053 | 0.008 | |
| -2.537 | -16.329 | 6.4364 | 19.309 | 0.020 | 0.003 | |
| -2.534 | -16.271 | 6.4212 | 19.2636 | 0.007 | 0.001 | |
| -2.533 |
Окончательно получим 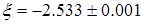 .
.
Пример 3.3.Методом итераций уточнить при 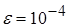 корень уравнения
корень уравнения 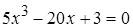 , изолированный на отрезке [0, 1].
, изолированный на отрезке [0, 1].
Решение
Приведем уравнение к виду 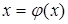 . Это можно сделать следующим образом:
. Это можно сделать следующим образом:
1. 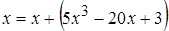 , тогда
, тогда 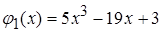 ;
;
