Элементы теории структурной

НАДЁЖНОСТИ

Надёжностью изделия в широком смысле называется способность изделия сохранять качество в течение определённого периода эксплуатации.

Математической надёжностью изделия за время t называется вероятность его безотказной работы за это время.

Для анализа надёжности составляется структурная схема изделия. При этом различают последовательное и параллельное соединения элементов системы в смысле надёжности.

Последовательным называется такое соединение элементов в системе, при котором отказ любого из них приводит к отказу системы.

При последовательном соединении надёжность системы P выражается через надёжности элементов 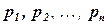по формуле .

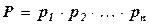Параллельным называется такое соединение элементов в системе, при котором отказ системы наступает только при отказе всех её элементов.

При параллельном соединении надёжность системы P выражается по формул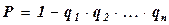е , где .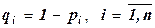

7.1. Система состоит из трёх элементов, отказы которых независимы, а вероятности отказов равны 0,1, 0,2, 0,3. Для отказа системы достаточно, чтобы отказал любой из её элементов. Найти надёжность системы.

7.2. Система состоит из трёх элементов, отказы которых независимы, а вероятности отказов равны 0,2, 0,1, 0,5. Отказ системы наступает тогда, когда отказывают все три элемента. Найти надёжность системы.

7.3. Определить надёжность системы.

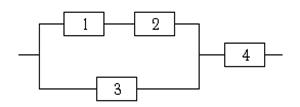Надёжности элементов равны:

p₁ = 0,8; p₂ = 0,7; p₃ = 0,9; p₄ = 0,6.

7.4. Определить надёжность системы.

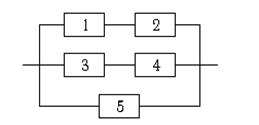Надёжности элементов равны:

p₁ = 0,8; p₂ = 0,9; p₃ = 0,7;

p₄ = 0,6; p₅ = 0,5.

7.5. Определить надёжность системы.

Надёжности элементов равны:

p₁ = 0,7; p₂ = 0,8; p₃ = 0,6;

p₄ = 0,7; p₅ = 0,8.

7.6. Прибор состоит из двух узлов, отказы которых независимы, и выходит из строя, если откажет хотя бы один узел. Вероятность безотказной работы первого узла в течение времени t равна 0,8, второго – 0,7. Прибор испытывался в течение времени t, в результате чего он вышел из строя. Найти вероятность того, что отказал только первый узел.

7.7. Система испытывалась в течение времени t, в результате чего она вышла из строя. Найти вероятность того, что отказали только элементы с номерами 2 и 4.

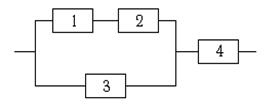Надёжности элементов равны:

p₁ = 0,6; p₂ = 0,8; p₃ = 0,7; p₄ = 0,9.

7.8. Система состоит из пяти элементов, отказы которых независимы, а вероятности отказов за время t одинаковы и равны 0,3. Отказ системы наступает лишь тогда, когда выходят из строя по меньшей мере три элемента из пяти. Найти надёжность системы за время t.

7.9. Прибор может работать в двух режимах: нормальном и с перегрузкой. Нормальный режим наблюдается в 80% всех случаев включения прибора. Вероятность выхода из строя за время t в нормальном режиме равна 0,1, в режиме с перегрузкой – 0,7. Определить надёжность прибора за время t.

7.10. В прибор входят 3 одинаковых лампы, вероятность перегорания каждой из которых равна 0,3 и перегорания независимы. Если перегорит только одна лампа, то прибор выходит из строя с вероятностью 0,4, только две – с вероятностью 0,7. Если перегорят все лампы, то прибор обязательно выйдет из строя. Найти вероятность того, что прибор выйдет из строя.

7.11. Определить надёжность системы.

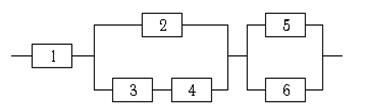Надёжности элементов равны:

p₁ = 0,7; p₂ = 0,8; p₃ = 0,6;

p₄ = 0,7; p₅ = 0,9; p₆ = 0,9.

7.12. Прибор состоит из двух узлов, отказы которых независимы, и выходит из строя, если откажет хотя бы один узел. Вероятность безотказной работы первого узла в течение времени t равна 0,8, второго – 0,7. Прибор испытывался в течение времени t, в результате чего он вышел из строя. Найти вероятность того, что отказали оба узла.

7.13. Определить надёжность системы.

Надёжности элементов равны:

p₁ = 0,9; p₂ = 0,9; p₃ = 0,8;

p₄ = 0,8; p₅ = 0,7.

7.14. Изделие можно разбить на три блока, отказы которых за время t независимы, а вероятности отказов равны соответственно 0,2, 0,3, 0,1. Найти надёжность изделия в следующих случаях: а) изделие выходит из строя, если отказывает хотя бы один из трёх выделенных блоков; б) изделие выходит из строя лишь тогда, когда отказывают все три блока; в) для выхода изделия необходимо, чтобы вышли из строя по меньшей мере два из трёх блоков.

7.15. Система испытывалась в течение времени t, в результате чего она вышла из строя. Найти вероятность того, что отказали только элементы с номерами 2 и 5.

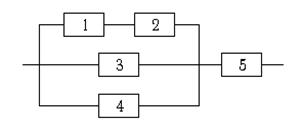Надёжности элементов равны:

p₁ = 0,9; p₂ = 0,8; p₃ = 0,5;

p₄ = 0,4; p₅ = 0,7.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайнойвеличиной называется величина, которая в результате эксперимента может принять то или иное значение, заранее неизвестно какое.

Закономраспределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Функцияраспределения случайной величины Х обозначается F(x) и определяется равенством P{X<x}.

Свойства функции распределения:

1) 0 £ F(x) £ 1;

2) F(x₁)£F(x₂), если x₁£x₂;

3) , ;

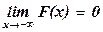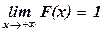4) F(x) непрерывна слева: .

Вероятность попадания случайной величины Х на числовой промежуток [a; b) вычисляется по формуле 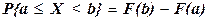.