Метод наименьших квадратов. В лабораторных работах по физике, измерение какой-либо физической величины обычно проводят несколько раз при различных условиях
ЛАБОРАТОРНАЯ РАБОТА № 19
В лабораторных работах по физике, измерение какой-либо физической величины обычно проводят несколько раз при различных условиях, а найденный результат записывают в виде 20,3±2,3. Это необходимо для того, чтобы нейтрализовать погрешности приборов, трясущиеся руки экспериментатора, вспышки на солнце и так далее.
Метод наименьших квадратов (далее МНК) является одним из способов противостоять ошибкам измерений.
Общая формулировка метода выглядит так:
Пусть имеется система уравнений:
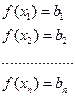
Здесь f(x) эта некая функция, конкретный вид которой не известен, известен лишь ее общий вид, например известно что это прямая, или многочлен, или синусоида и так далее. МНК позволяет зная общий вид функции найти ее конкретный вид (коэффициенты) который наилучшим образом вписывается в экспериментальные данные.
Особенностью МНК является то, что число уравнений превышает число неизвестных коэффициентов в функции f(x). Таким образом, в общем случае точного решения системы не существует.
Обратите внимание, что система решается не относительно xn, а относительно неизвестных коэффициентов функции f(x).
Основная идея МНК состоит в том, чтобы при нахождении конкретного вида функции минимизировать сумму квадратов ошибок во всех исходных уравнениях.
Иными словами нужно свести к минимуму функцию:
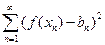
Может возникнуть вопрос почему сумма квадратов? Во-первых, квадрат любого числа всегда неотрицателен, и следовательно сумма квадратов всегда не отрицательна, т.е. ограничена снизу, а следовательно у нее есть минимум; во-вторых, при нахождении минимальной суммы квадратов мы уменьшаем максимальную ошибку.
Иметь в двух точках ошибку в 5 единиц, лучше, чем в первой точке иметь нулевое отклонение, зато во второй точке иметь отклонение 10. Сумма отклонений в обоих случаях будет одинаковой, а вот сумма квадратов отклонений в первом случае будет меньше.
Чтобы визуально понять что такое МНК, можно поиграть с функцией «Линия тренда» в Microsoft Excel.
Пример. Пусть имеются результаты некого физического эксперимента. Представим, что мы измеряли значение параметра Y при различных значениях параметра X.
| X | Y |
| 1.1 | |
| 1.98 | |
| 3.2 |
Пусть, мы так же знаем, что теоретически эти параметры связаны линейной зависимостью:
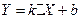
Параметров k и b мы не знаем, их предстоит найти.
Если построить график этой зависимости, то будет видно, что точки лежат примерно на одной прямой.
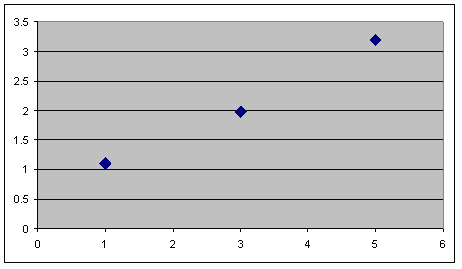
Ключевое слово здесь – примерно. Как известно, чтобы построить прямую, достаточно двух точек. Если мы попытаемся найти уравнение прямой, выбирая две точки из представленных трех, оставшаяся не будет удовлетворять найденному уравнению прямой. Таким образом можно заключить, что найти прямую, проходящую точно через три данные точки не возможно.
Придется искать прямую, проходящую примерно через данные точки при помощи МНК.
Составим дополнительную таблицу.
| X | Y | Ошибка | Квадрат ошибки |
| 1.1 | k * 1 + b - 1.1 | (k * 1 + b - 1.1)2 | |
| 1.98 | k * 3 + b - 1.98 | (k * 3 + b - 1.98)2 | |
| 3.2 | k * 5 + b - 3.2 | (k * 5 + b - 3.2)2 | |
| Сумма | (k * 1 + b - 1.1)2 + (k * 3 + b - 1.98)2 + (k * 5 + b - 3.2)2 |
Таким образом, задача состоит в том, чтобы найти такие k и b, чтобы сумма представленная в последней строке (назовем ее функцией ошибки) таблицы была минимальной.
Как известно из курса математического анализа, экстремум (минимум или максимум) функция многих переменных достигает в точке, где ее частные производные равны нулю.
Таким образом:
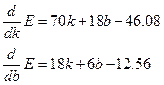
Приравнивая производные к нулю и получим систему уравнений:
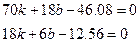
Решение которой находится тривиально. Таким образом получим, что k=0.525, b=0.518. Вообще говоря, в общем случае, нужно еще доказать, что это именно минимум, и что это минимум глобальны (в случае если система имеет несколько решений). Однако, если мы в заданный набор данных пытаемся вписать полином, то найденное решении и будет глобальным минимумом.
Тогда уравнение прямой запишется:
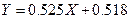
На графике это будет выглядеть следующим образом:
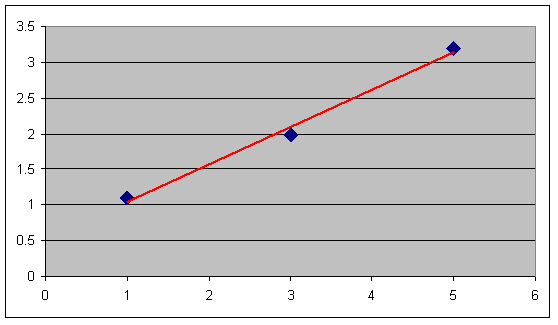
Как видно из рисунка, найденная прямая, довольно не плохо вписывается в наш набор точек.
Пример 1.
Пусть имеются результаты некого физического эксперимента. Представим, что мы измеряли значение параметра Y при различных значениях параметра X.
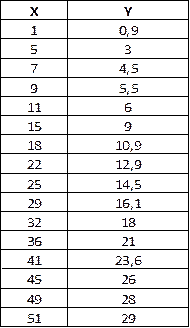
Создаем книгу MS Excel, вносим результаты эксперимента в ячейки.
В А2 вносим Х, в В2 вносим Y. В диапазон А3:А18 вносим значения Х, в диапазон В3:В18 значения Y.
Лист рабочий книги примет вид:
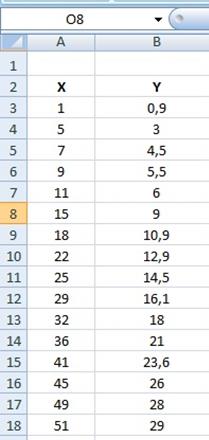
Рис.5. Таблица значений эксперимента
Далее по данным строим график, тип выбираем точечный. Результат представлен на рисунке 6.
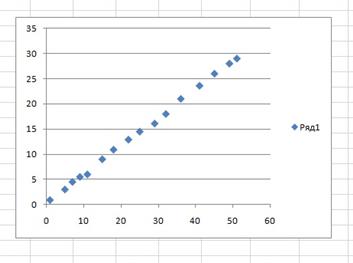
Рис.6. График значений эксперимента
Для использования МНК строим линию тренда, для этого выделяем на графике значения, по правой кнопки мыши вбираем функцию Добавить линию тренда. В итоге перед нами появится окно настройки линии тренда. Устанавливаем флажок в положение – Показывать уравнение на диаграмме, окно настройки представлено на рисунке 7.
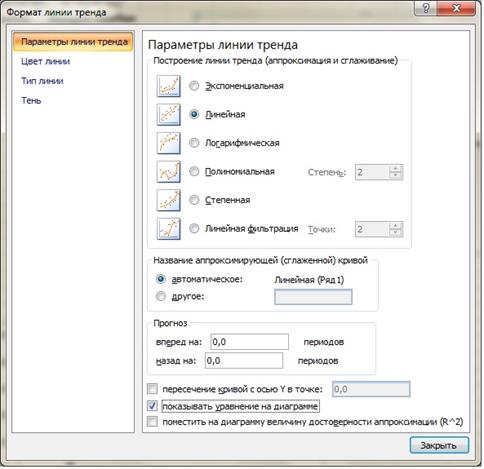
Рис.7. Окно настройка линии тренда
При нажатии кнопки закрыть, необходимая линия тренда отобразится на графике, уравнение будет подписано рядом (рисунок 8).
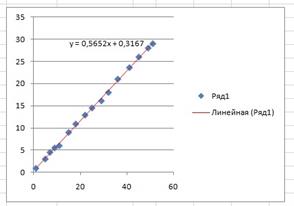
Рис.8. Окно настройка линии тренда
Далее нам необходимо посчитать значение функции (линии тренда) в точках Y, чтоб найти отклонение. Для этого в ячейки: E1, F1 для удобства ввода вносим формулы расчетов: k * A3 + b – B3; (k * A3 + b – B3)2. В ячейки D2, E2, F2 вводим: Линейная, Ошибка, Квадрат ошибки. В ячейки D3, E3, F3 вводим формулы расчетов: =0,5652*A3+0.3167; =0.5652*A3+0.3167-B3; =E3*E3. При помощи автозаполнения копируем формулы из диапазона D3:F3 в диапазон D4: F18. В ячейку А19 ввести слово сумма, в ячейке F19 посчитать автосумму столбца F. Результат вычислений представлен на рисунке 9.
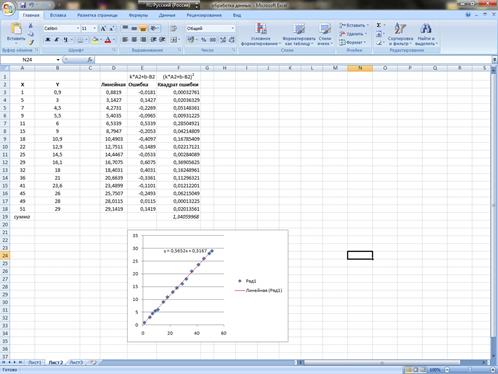
Рис.9. Итоговое окно.
Дополнительно рассмотреть другие типы линии, посчитать отклонение, выбрать наиболее подходящий вид линии тренда (т.е. с наименьшим отклонением).
Пример изображен на рисунке 10.
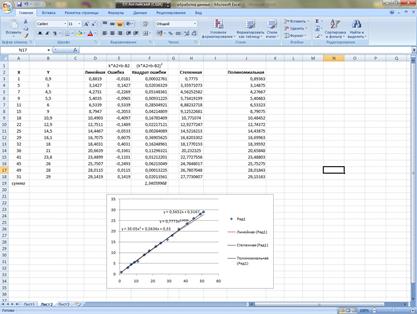
Рис.9. Линия тренда (степенная)
Задание для самостоятельной работы:
Определить наилучший вид линии тренда (полиномиальная степени 2-3, линейная). Определить расхождение в вычислениях.
| 0,5 | -4,90125 | 0,5 | -5 | -0,5 | -5,16625 | |||
| 1,1 | -4,30161 | 1,1 | -4,5 | -1,1 | -6,02509 | |||
| 1,6 | -2,92576 | 1,6 | -3 | -1,6 | -7,76544 | |||
| 1,9 | -1,53649 | 1,9 | -1,6 | -1,9 | -9,43821 | |||
| 2,3 | 1,15503 | 2,3 | 1,2 | -2,3 | -12,58333 | |||
| 2,8 | 6,15968 | 2,8 | 6,2 | -2,8 | -18,27648 | |||
| 3,5 | 16,95375 | 3,5 | 16,9 | -3,5 | -30,26125 | |||
| 3,9 | 25,48591 | 3,9 | -3,9 | -39,59261 | ||||
| 4,3 | 35,99663 | 4,3 | -4,3 | -50,98893 | ||||
| 0,5 | -4,14075 | 0,5 | -4,2 | -0,5 | -0,158 | |||
| 1,1 | -5,01471 | 1,1 | -5 | -1,1 | 0,0376 | |||
| 1,6 | -3,73056 | 1,6 | -3,7 | -1,6 | 0,3986 | |||
| 1,9 | -2,08191 | 1,9 | -2 | -1,9 | 0,7016 | |||
| 2,3 | 1,14081 | 2,3 | 1,2 | -2,3 | 1,2064 | |||
| 2,8 | 6,81576 | 2,8 | 6,9 | -2,8 | 1,9994 | |||
| 3,5 | 17,83425 | 3,5 | 17,8 | -3,5 | 3,412 | |||
| 3,9 | 25,74049 | 3,9 | 25,8 | -3,9 | 4,3776 | |||
| 4,3 | 34,81761 | 4,3 | -4,3 | 5,4584 | ||||
| 0,5 | -0,5 | 0,5 | -0,6 | -0,5 | 0,8 | |||
| 1,1 | 2,5 | 1,1 | 2,5 | -1,1 | 0,45 | |||
| 1,6 | 1,6 | -1,6 | 0,21 | |||||
| 1,9 | 6,5 | 1,9 | 6,5 | -1,9 | 0,06 | |||
| 2,3 | 8,5 | 2,3 | 8,6 | -2,3 | -0,15 | |||
| 2,8 | 2,8 | 11,1 | -2,8 | -0,5 | ||||
| 3,5 | 14,5 | 3,5 | 14,45 | -3,5 | -0,76 | |||
| 3,9 | 16,5 | 3,9 | 16,4 | -3,9 | -0,96 | |||
| 4,3 | 18,5 | 4,3 | 18,4 | -4,3 | -1,2 | |||
| 0,5 | -0,2 | -0,5 | -0,6 | -0,5 | -0,2 | |||
| 1,1 | 0,04 | -1,1 | 2,5 | -1,1 | 0,04 | |||
| 1,6 | 0,4 | -1,6 | -1,6 | 0,4 | ||||
| 1,9 | 0,8 | -1,9 | 6,5 | -1,9 | 0,8 | |||
| 2,3 | 1,2 | -2,3 | 8,6 | -2,3 | 1,2 | |||
| 2,8 | -2,8 | 11,1 | -2,8 | |||||
| 3,5 | 3,5 | -3,5 | 14,45 | -3,5 | 3,5 | |||
| 3,9 | 4,5 | -3,9 | 16,4 | -3,9 | 4,5 | |||
| 4,3 | 5,5 | -4,3 | 18,4 | -4,3 | 5,5 | |||
| 0,5 | 0,8 | -0,5 | 0,75 | -0,5 | -5 | |||
| 1,1 | 0,45 | -1,1 | 0,45 | -1,1 | -6 | |||
| 1,6 | 0,21 | -1,6 | 0,2 | -1,6 | -7,7 | |||
| 1,9 | 0,06 | -1,9 | 0,05 | -1,9 | -9,5 | |||
| 2,3 | -0,15 | -2,3 | -0,15 | -2,3 | -12,4 | |||
| 2,8 | -0,5 | -2,8 | -0,4 | -2,8 | -18,3 | |||
| 3,5 | -0,76 | -3,5 | -0,75 | -3,5 | -30,1 | |||
| 3,9 | -0,96 | -3,9 | -0,95 | -3,9 | -39,6 | |||
| 4,3 | -1,2 | -4,3 | -1,15 | -4,3 | -50,98 |
