Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число
Определители
Понятие определителя квадратной матрицы A порядка n = 1,2,3,...
Определитель – это некоторое число поставленное в соответствие квадратной матрице 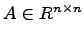 .
.
Для неквадратных матриц понятие определителя не вводится.
Для обозначения определителя квадратной матрицы A будем пользоваться обозначением 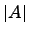 или
или 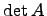 .
.
Пусть A - произвольная квадратная матрица порядка n.
Если n=1, то матрица A состоит из одного числа A. Положим по определению, что определитель такой матрицы равен числу A, т.е. 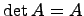 .
.
Если n=2, то матрица A имеет вид
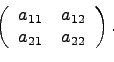
Положим по определению, что определитель такой матрицы равен
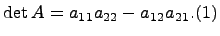
Если n=3, то матрица A имеет вид
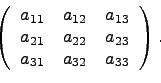
Положим по определению, что определитель такой матрицы равен
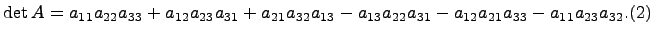
Основные свойства определителей.
Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании:
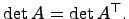
Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка. Непосредственная проверка доказывает данное свойство.
Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю.
Свойство 2 непосредственно вытекает из определения определителя.
Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.
Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.
Свойство 5. Если каждый элемент i-й строки (столбца) матрицы A представлен в виде суммы двух слагаемых, то определитель такой матрицы равен 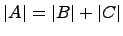 , где элементы матриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.
, где элементы матриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.
Отметим некоторые следствия, непосредственно вытекающие из перечисленных 5 основных свойств определителя.
Следствие 1. Определитель матрицы, имеющей две одинаковые строки (столбца) равен нулю.
Доказательство. Пусть A - квадратная матрица, имеющая две одинаковые строки (столбца). B - матрица полученная в результате перестановки указанных одинаковых строк (столбцов) матрицы A. Тогда, с одной стороны, 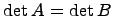 , с другой стороны, в силу свойства 3,
, с другой стороны, в силу свойства 3, 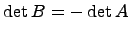 . Следовательно,
. Следовательно, 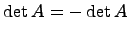 . Из последнего равенства следует, что
. Из последнего равенства следует, что 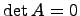 .
.
Следствие 2. Если какие-либо две строки (столбца) матрицы пропорциональны, то её определитель равен нулю.
Следствие 3. Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число 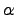 , то определитель не изменится.
, то определитель не изменится.
Миноры и алгебраические дополнения.
Пусть A - произвольная квадратная матрица, 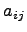 – её элемент, стоящий в позиции (I,j). Вычеркивая из матрицы A i-ю строку и j-ый столбец, получим некоторую матрицу
– её элемент, стоящий в позиции (I,j). Вычеркивая из матрицы A i-ю строку и j-ый столбец, получим некоторую матрицу 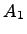 , порядка
, порядка 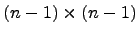 . Определитель матрицы
. Определитель матрицы 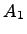 называется минором элемента
называется минором элемента 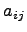 . Минор элемента
. Минор элемента 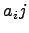 будем обозначать символом
будем обозначать символом 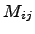 .
.
Число 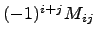 называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 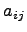 . Для обозначения алгебраического дополнения элемента
. Для обозначения алгебраического дополнения элемента 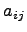 будем пользоваться символом
будем пользоваться символом 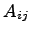 .
.
Разложение определителя по строке (столбцу)
