Графический метод для поиска корней
Содержание
Введение 3
Задание 1. Приближенное решение конечных уравнений 4
Задание 2. Методы численного интегрирования 11
Задание 3. Метод наименьших квадратов 17
Задание 4. Методы численного решения дифференциальных уравнений с помощьюMS Excel 21
Задание 5. Построение поверхности 25
Задание 6. Решение задач оптимизации с помощью надстройки Поиск решения 29
Задание 7. Функции просмотра и ссылок 34
Список литературы
Введение
Учебно-ознакомительная практика студентов предполагает применение знаний, полученных студентами за время обучения, для решения практических задач. Во время прохождения практики студенты должны изучить численные методы решения инженерных задач и приобрести навыки их применения: методы решения трансцендентных уравнение, методы численного интегрирования, методы решения дифференциальных уравнений.
Студенты на различных примерах изучают широкие возможности MS Excel для решения математических, экономических и других задач. Представленные в методическом пособии задания предназначены для углубленного освоения возможностей табличного процессора и интегрированных сред разработки программных средств.
При прохождении практики студент должен представить письменный отчет по каждому заданию. Отчет должен содержать:
формулировку задачи;
описание метода;
программу на одном из языков программирования или (и) таблицу решения;
результаты работы программы.
Описание каждого задания содержит необходимую для его выполнения информацию из сопутствующего курса, пример решения аналогичной задачи. Некоторые задания предполагают наряду с MS Excel использование алгоритмического языка для выполнения. Также приводятся практические примеры применения методов и функций.
Задание 1. Приближенное решение конечных уравнений
Цель работы: научиться выполнять типовые задачи вычислительной математики, решение алгебраических и трансцендентных уравнений, часто встречающихся в инженерной практике.
Рассматривается численное решение уравнений вида
f(x)=0, (1.1)
где f – заданная функция.
Если уравнение (1.1) имеет следующий вид:
A 0 + A 1 x + A 2 x 2 + . . . + A n x n = 0,
(где A i -известные коэффициенты), то оно называется алгебраическим уравнением n-ой степени. Во всех других случаях уравнение (1.1) называется трансцендентным
Наиболее универсальные методы решения уравнений вида (1.1): метод Ньютона, метод дихотомии, метод хорд, метод простой итерации.
Метод Ньютона. Очередное приближение корня уравнения находится по формуле
хn+1=xn-f(xn)/f 1(xn).
Метод дихотомии (метод деления отрезка пополам). На каждой итерации отрезок [a,b] делится пополам и выбирается та из половин, на концах которой функция f(x) имеет значения разных знаков.
Метод хорд. Очередное приближение находится по формуле
хn+1=xn- (xn – xn-1)* f (xn)./ (f(xn)- f(xn-1)).
Метод простой итерации. Очередное приближение корня находится по формуле
xn= w(xn-1);
начальное приближение можно найти графически. Метод сходится, если |w1(х)| <1 в окрестности корня.
Численное решение уравнения (1) обычно начинают с нахождения грубого решения – начального приближения.
Пример.
Дано уравнение
х3-17х+12=0 (1.2)
Перед решением уравнения численным методом его нужно привести к стандартной форме. Будем рассматривать две стандартные формы.
Таблица 1.1 – Стандартные формы уравнений
| Форма | Пример | Где используется |
| 1 уравнение с нулевой правой частью | х3-17х+12=0 | Графический метод, метод хорд, дихотомии, Пакет Поиск решения |
| 2 уравнение, в левой части которого стоит неизвестная величина | х3+12 х=w(х)=---------- | Метод итерации в ячейке |
Для решения заданного примера рассмотрим следующие способы:
1. Поиск корней уравнения с помощью графика (можно рассматривать как начальное приближение);
2. Метод итерации.
3. Решение уравнения с помощью надстройки Поиск решения.
4. Программа на языке С++ (метод половинного деления – дихотомия).
Графический метод для поиска корней
При использовании графического метода для поиска корней удобна первая форма уравнения, в которой все его члены перенесены в одну часть.
Уравнение переписывается в виде
f(x)= х3-17х+12. (1.3)
Вводится в электронную таблицу столбец значений х в интервале -5 <=x <=5, затем для каждого х вычисляется значение f(x). Строится точечная диаграмма - график функции f(x).
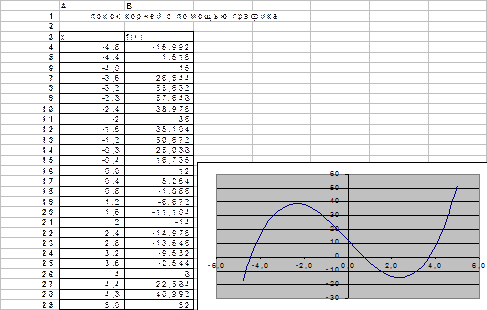
Рисунок 1.1
Из графика видно, что корни находятся возле точек х=0,8, х=3,7 и х=-4,5.
Графический метод нахождения корней прост, но не совсем точен. Для нахождения корней с более высокой точностью применяются численные итерационные методы. Применяя эти методы, следует указывать начальные приближения, замечательным средством получения которых является графический метод.
Методы итерации
Суть метода простой итерации (метод прямой подстановки) – использование вычисленного на предыдущем шаге значения в качестве предполагаемого значения для последующей итерации. Для этого следует применить стандартную форму 2 -
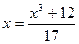 (1.4)
(1.4)
Изолированная переменная в левой части уравнения называется вычисляемым значением. Обозначим ее хв. Переменная х в правой части уравнения называется предполагаемым значением. Обозначается как хп .
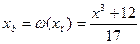 (1.5)
(1.5)
В ячейке А4 вводится начальное предполагаемое значение – (0,8). Для вычисления в ячейке В4 вычисляемого значения по формуле (1.5) используется предполагаемое значение в ячейке А4.
Каждое новое предполагаемое значение, содержащееся в столбце А, равно вычисляемому значению предыдущего шага из столбца В. Например, в ячейке А5 – вводится формула (=В4).
Чтобы получить новое вычисляемое значение, скопировать формулу из ячейки В4 в ячейку В5.
Для последующих итераций ячейки копируются по мере необходимости из строки 5 в нижние строки. Разность хп-хв в столбце С позволяет оценить скорость сходимости метода.
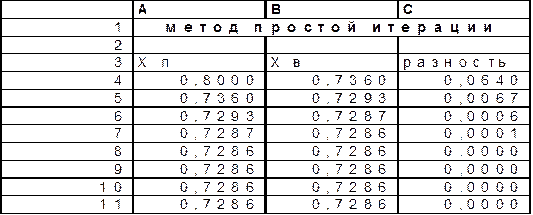 |
Рисунок 1.2
Из рисунка 1.2 видно, что с помощью метода простой итерации (прямой подстановки) удалось найти корень х=0,7286 всего за несколько шагов.
Так как w1(x)= 3*х2 /17 <1 в окрестности х=0,8, то необходимое условия для сходимости метода выполнено.
Преимущество метода простой итерации – легко осуществим в электронной таблице.
Недостатки: иногда метод расходится – с его помощью нельзя получить все корни.
1.3 Надстройка Поиск решения
Программа MS Excel предоставляет другой метод – Надстройка Поиск решения. Этот метод устраняет недостатки метода простой итерации.
Примечание: эта надстройка не устанавливается по умолчанию и не активизируется по умолчанию. Чтобы активизировать надстройку Поиск решения, надо выполнить: Сервис – Надстройки- в окне со списком Надстройки установить флажок Поиск решения.
Уравнение записывается в форме 1. В ячейку В3 вводится начальное приближение - (0,8), а в ячейку В4 – формула =В3^3-17*В3+12 (рисунок 1.3).

Рисунок 1.3
Далее Сервис – Поиск решения.
В поле Установить целевую ячейку в качестве целевой ячейки выбирается ячейка В4, содержащая формулу.
Надстройка Поиск решения будет продолжать поиск решения, пока значение в целевой ячейке не будет равным нулю (так как в правой части уравнения стоит ноль).
Для этого переключатель устанавливается в положение по значению:, а в соответствующем поле введено значение 0.
В поле Изменяя ячейки: вводится адрес ячейки, в которой находится предполагаемое значение, - В3.
После ввода всех параметров щелкнуть на кнопке Выполнить.
С помощью надстройки Поиск решения найден корень, равный 0,73.
Чтобы найти другие корни, следует изменить предполагаемое значение и повторно запустить надстройку Поиск решения.
Преимущества надстройки Поиск решения: проста в применении и позволяет найти все корни уравнения.
1.4 Алгоритм деления отрезка пополам (метод дихотомии)
Требуется определить значение корня с погрешностью, не превосходящей данного положительного числа e. Можно применить метод деления отрезка пополам.
Взяв середину отрезка [a,b], на котором находится корень, то есть точку с координатой с=(а+b)/2, можно сузить диапазон поиска корня: перейти от отрезка [a,b] к отрезку [a,c] или [c,b] в зависимости от знака f (с): если f(a)f(c)<0, то перейти к отрезку [а,с], если f(a)f(c)>0, то перейти к отрезку [c,b]. Если затем найти середину меньшего отрезка и вычислить для нее значение функции f(x), то можно будет вновь сузить диапазон поиска и так далее. После нескольких шагов получится отрезок, длина которого будет меньше данного числа e.
Использование этого метода демонстрируется на программе, написанной на алгоритмическом языке (С++).
Схема программы, реализующий этот алгоритм. Для переменных a и b остаются в силе неравенства a<b и f(a)f(b)[0. Значением fa является f (a), с – обозначает середину отрезка [a,b], fc принимает значение, равное f(c).
Эта программа позволяет получать один из корней. Поэтому предварительно надо определить границы а и b настолько точно (можно использовать графический метод), что в отрезке содержался ровно один корень. Это позволит, задавая различные а и b, получать различные корни.
Для конкретной функции f(x)=x3-17*x+12; один из корней принадлежит отрезку [0,2]; а=0,b=2. тогда программа примет следующий вид.
#include<iostream.h>
#include<conio.h>
#include<math.h>
float f(float x) //функция, вычисляющая значение конкретной функции
{float ff;
ff=x*x*x-17*x+12;
return ff;}
void main() // Главная функция
{float a,b,c,fa,fc,eps; int n=0;
clrscr();
cin>>a>>b>>eps;
fa=f(a);
do
{ c=(b+a)/2;
fc=f(c);
if (fa*fc<0) b=c;
else
{
a=c;fa=fc;
} cout<<c<<endl;n=n+1;
} while (b-a>eps) ;
cout<<a<<endl;
cout<<n<<endl;
}
Преимущества метода: легко осуществим и в электронной таблице, и на языке С++. На языке С++ позволяет найти все корни.
Недостатки метода: по приближенному значению f(x) не всегда можно установить, справедливо ли неравенство f(x)<= 0, когда f(x) мало и погрешность вычисления значения f(x) превосходит само это значение.
