ЛАБОРАТОРНАЯ РАБОТА №3 НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ МНОГОЧЛЕНОВ
Пусть даны ненулевые многочлены f(x) и φ(x). Если остаток от деления f(x) на φ(х) равен нулю, то многочлен φ(х) называется делителем многочлена f(х). Имеет место следующее утверждение: многочлен φ(х) тогда и только тогда будет делителем многочлена f(х), когда существует многочлен ψ(х), удовлетворяющий равенству f(х)=φ(х)ψ(х). Многочлен φ(х) называется общим делителем произвольных многочленов f(x) и g(x), если он является делителем каждого из этих многочленов. Согласно свойствам делимости, к числу общих делителей многочленов f(x) и g(x) принадлежат все многочлены нулевой степени. Если эти многочлены не имеют других общих делителей, то их называют взаимно простыми и записывают (f(x), g(x))=1. В общем же случае многочлены f(x) и g(x) могут обладать общими делителями, зависящими от х.
Как и для целых чисел, для многочленов вводится понятие их наибольшего общего делителя. Наибольшим общим делителем отличных от нуля многочленов f(x) и g(x) называется такой их общий делитель d(x), который делится на любой общий делитель этих многочленов. Наибольший общий делитель многочленов f(x) и g(x) обозначают символами НОД, d(x), (f(x), g(x)). Заметим, что такое определение НОД имеет место и для целых чисел, хотя чаще используется другое, известное всем студентам.
В связи с этим определением возникает ряд вопросов:
1. Существует ли НОД для произвольных ненулевых многочленов f(x) и g(x)?
2. Как найти НОД многочленов f(x) и g(x)?
3. Сколько наибольших общих делителей имеют многочлены f(x) и g(x)? И как найти их?
Существует способ нахождения НОД целых чисел, называемый алгоритмом последовательного деления или алгоритмом Евклида. Он применим и к многочленам, состоит в следующем.
Алгоритм Евклида. Пусть даны многочлены f(x) и g(x), степень f(х)≥степени g(x). Делим f(x) на g(x), получаем остаток r1(x). Делим g(x) на r1(x), получаем остаток r2(x). Делим r1(x) на r2(x). Так продолжаем деление до тех пор, пока не совершится деление нацело. Тот остаток rk(x), на который нацело делится предыдущий остаток rk-1(x), и будет наибольшим общим делителем многочленов f(x) и g(x).
Сделаем следующее замечание, полезное при решении примеров. Применяя алгоритм Евклида к многочленам для нахождения НОД, мы можем, чтобы избежать дробных коэффициентов, умножить делимое или сократить делитель на любое не равное нулю число, причем, не только начиная какое-либо из последовательных делений, но и в процессе самого этого деления. Это будет приводить к искажению частного, но интересующие нас остатки будут приобретать лишь некоторый множитель нулевой степени, что, как мы знаем, допускается при разыскивании делителей.
Пример 1. Найти НОД многочленов f(x)=x3–x2–5x–3,
g(x)=x2+x–12. Делим f(x) на g(x):
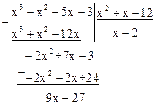 .
.
Первый остаток r1(x) после сокращения на 9 будет х–3. Делим g(x) на r1(x):
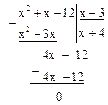 .
.
Деление произошло нацело. Следовательно, r1(x)=х–3 есть НОД многочленов x3–x2–5x–3 и x2+x–12.
Пример 2. Найти НОД многочленов f(x)=3x3+2x2–4x–1,
g(x)=5x3–3x2+2x–4. Умножаем f(x) на 5 и делим 5f(x) на g(x):
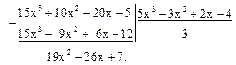
Первый остаток r1(x) будет 19х2–26х+7. Делим g(x) на первый остаток, предварительно умножив g(x) на 19:
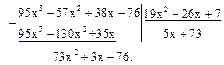
Умножаем на 19 и продолжаем деление:
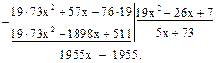
Сокращаем на 1955 и получаем второй остаток r2(x)=х-1. Делим r1(x) на r2(x):
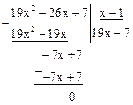 .
.
Деление совершилось нацело, следовательно, r2(x)=х-1 есть НОД многочленов f(x) и g(x).
Пример 3. Найти НОД многочленов f(x)=3x3–x2+2x–4,
g(x)=x3–2x2+1.
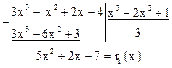 .
. 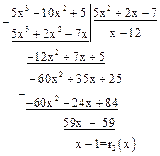 .
.
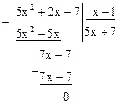 .
.
Ответ: (f(x), g(x))=х–1.
Этот способ нахождения НОД показывает, что если многочлены f(x) и g(x) имеют оба рациональные или действительные коэффициенты, то и коэффициенты их наибольшего общего делителя также будут рациональными или, соответственно, действительными.
Многочлены f(x), g(x) и d(x) связаны следующим соотношением, которое часто используется в различных вопросах и описывается теоремой.
Если d(x) есть наибольший общий делитель многочленов f(x) и g(x), то можно найти такие многочлены u(x) и v(x), что f(x)u(x)+g(x)v(x)=d(x). Можно считать при этом, если степени многочленов f(x) и g(x) больше нуля, то степень u(x) меньше степени g(x), а степень v(x) меньше степени f(x).
Покажем на примере, как найти многочлены u(x) и v(x) для заданных многочленов f(x) и g(x).
Пример 4. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), если
A) f(x)=х4-3х3+1, g(x)=х3-3х2+1;
B) f(x)=х4-х3+3х2-5х+2, g(x)=х3+х-2.
А. Находим НОД многочленов f(x) и g(x), пользуясь алгоритмом Евклида, только теперь в процессе деления нельзя производить сокращение и домножение на подходящие числа, как мы делали в примерах 1, 2, 3.
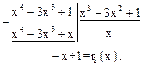 (1)
(1) 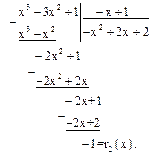 (2)
(2)
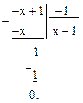 (3)
(3)
Таким образом, общим делителем многочленов f(x) и g(x) является –1.
Согласно произведенному делению записываем равенства:
f(x)=g(x)х+(–х+1) (1*)
g(x)=(–х+1)(–х2+2х+2)–1 . (2*)
Из равенства (2*) выразим d(x)= –1=g(x)–(–x+1)(–x2+2x+2). Из равенства (1*) находим –х+1=f(x)–g(x)х и подставляем его значение в равенство (2*): d(x)= –1=g(x)–(f(x)–g(x)х)(–x2+2x+2).
Теперь группируем слагаемые в правой части относительно f(x) и g(x):
d(x)= –1=g(x)–f(x)(–x2+2x+2)+g(x)x(–x2+2x+2)=f(x)(x2–2x–2)+g(x)(1–x3 +2x2+2x)=f(x)(x2–2x–2)+g(x)(–x3+2x2+2x+1).
Следовательно, u(x)=x2–2x–2, v(x)= –x3+2x2+2x+1.
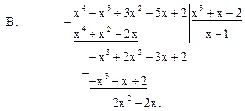
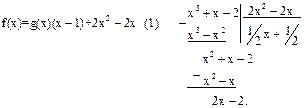
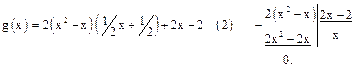
Наибольшим общим делителем многочленов f(x) и g(x) является многочлен 2х-2. Выражаем его, используя равенства (1) и (2):
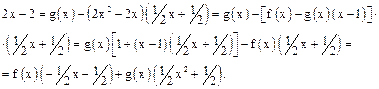
Ответ: 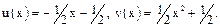
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ
Вариант 1
1. Найти НОД многочленов:
а) х4–2х3–х2–4х–6, 2х4–5х3+8х2–10х+8.
б) (х–1)3(х+2)2(2х+3), (х–1)4(х+2)х.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=х6-4х5+11х4-27х3+37х2-35х+35,
g(x)=х5-3х4+7х3-20х2+10х-25.
Вариант 2
1. Найти НОД многочленов:
а) х4-3х3-3х2+11х-6, х4–5х3+6х2+х-3.
б) (2х+3)3(х-2)2(х+1) и его производной.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x),g(x)), если
f(x)=3х7+6х6-3х5+4х4+14х3-6х2-4х+4, g(x)=3х6-3х4+7х3-6х+2.
Вариант 3
1. Найти НОД многочленов:
а) 2х4+х3+4х2-4х-3, 4х4-6х3-4х2+2х+1.
б) (х+1)2(2х+4)3(х+5)5, (х-2)2(х+2)4(х-1).
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=3х3-2х2+2х+2, g(x)=х2-х+1.
Вариант 4
1. Найти НОД многочленов:
а) 3х4-83+7х2-5х+2, 3х4-2х3-3х2+17х-10.
б) (х+7)2(х-3)3(2х+1) и его производной.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=х4-х3-4х2+4х+1, g(x)=х2-х-1.
Вариант 5
1. Найти НОД многочленов:
а) 2х4-3х3-х2+3х-1, х4+х3-х-1.
б) х4(х-1)2(х+1)3, х3(х-1)3(х+3).
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=3х5+5х4-16х3-6х2-5х-6, g(x)=3х4-4х3-х2-х-2.
Вариант 6
1. Найти НОД многочленов:
а) х4-2х3+4х2-2х+3, х4+5х3+8х2+5х+7.
б) х3(х+1)2(х-1) и его производной.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=х5-5х4-2х3+12х2-2х+12, g(x)=х3-5х2-3х+17.
Вариант 7
1. Найти НОД многочленов:
а) х4+3х3-3х2+3х-4, х4+5х3+5х2+5х+4.
б) (2х+1)(х-8)(х+1), (х3+1)(х-1)2х3.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=4х4-2х3-16х2+5х+9, g(x)=2х3-х2-5х+4.
Вариант 8
1. Найти НОД многочленов:
а) х4-3х3-2х2+4х+6, 2х4-6х3+2х2-7х+3.
б) (х3-1)(х2-1)(х2+1), (х3+1)(х-1)(х2+2).
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=2х4+3х3-3х2–5х+2, g(x)=2х3+х2-х-1.
Вариант 9
1. Найти НОД многочленов:
а) 2х4+х3-5х2+3х+2, 3х4+8х3+3х2-3х-2.
б) (х3+1)(х+1)2(2х+3) и его производной.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=3х4-5х3+4х2–2х+1, g(x)=3х3-2х2+х-1.
Вариант 10
1. Найти НОД многочленов:
а) х4-5х3+7х2-3х+2, 2х4-х3-7х2+3х-2.
б) (х+1)(х2-1)(х3+1), (х3-1)(х2+х)х.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если
f(x)=х5+5х4+9х3+7х2+5х+3, g(x)=х4+2х3+2х2+х+1.
Вариант 11
1. Найти НОД многочленов:
а) 2х4-3х3+10х2-9х+12, 3х4+х3+10х2+3х+3.
б) (х3-8)(х3+1)(х+1), (х-2)2(х+3).
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если f(x)=х4+1, g(x)=х3+х.
Вариант 12
1. Найти НОД многочленов:
а) 2х4-х3-2х2-2х-1, 2х4-х3-5х2-4х-2.
б) (х+1)3(х2-1)х2 и его производной.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если f(x)=х4-х2+х-1, g(x)=х3-1.
Вариант 13
1. Найти НОД многочленов:
а) х4-2х3+2х2-1, 3х4-5х3+3х2+х-2.
б) (х3-1)(х-1)32х3 и его производной.
2. Найти многочлены u(x) и v(x) так, чтобы f(x)u(x)+g(x)v(x)=d(x), d(x)=(f(x), g(x)), если f(x)=х4-х3-х2-1, g(x)=х3+1.
